月月给华华出题---欧拉函数+分块+公式推导

原创已于 2022-04-02 08:22:29 修改 · 441 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2022-03-24 23:13:14 首次发布

数学专栏收录该内容

15 篇文章

订阅专栏

该博客介绍了计算小于n且与n互质的数的和的算法。通过欧拉phi函数预处理互质数的性质，并使用动态规划求解问题。代码中定义了phi数组来存储欧拉函数的结果，并使用了素数筛法来计算phi值。最终，程序输出所有满足条件的数的和。

与n互质而且小于n的所有数的和为 $p h i [n] * n / 2$
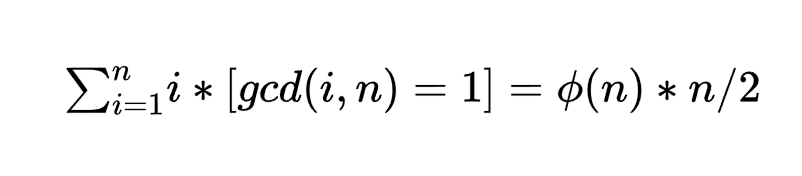
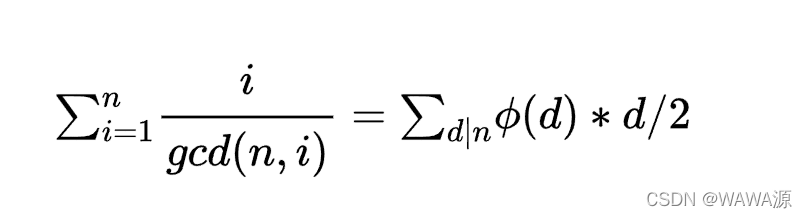
在这里插入图片描述

题目链接

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
const int mod = 1e9 + 7;
ll cnt,f[N],phi[N],prime[N];
bool vis[N];
void init(const int n = 1e6)
{
	phi[1] = 1;
	for (int i = 2; i <= n; i++)
	{
		if (!vis[i])
		{
			phi[i] = i - 1;
			prime[++cnt] = i;
		}
		for (int j = 1; j <= cnt && i <= n / prime[j]; j++)
		{
			vis[i * prime[j]] = 1;
			if (i % prime[j] == 0)
			{
				phi[i * prime[j]] = phi[i] * (prime[j]);
				break;
			}
			phi[i * prime[j]] = phi[i] * (prime[j] - 1);
		}
	}
}
int main()
{
	init();
	int n;
	cin >> n;
	for (int d = 1; d <= n; d++)
		for (int i = d; i <= n; i += d)
			f[i] += phi[d] * d / 2;
	for (int i = 1; i <= n; i++)
		printf("%lld\n", f[i] + 1);
	return 0;
}