【AI学习】梯度下降算法

一、引言

梯度下降（Gradient Descent）是机器学习和深度学习中最核心的优化算法之一。它通过迭代调整模型参数，逐步降低目标函数（损失函数）的值，最终找到参数的最优解（局部或全局最小值）。无论是线性回归、神经网络还是复杂深度学习模型，其训练过程都离不开梯度下降的核心思想。

---

二、核心原理

梯度下降的核心逻辑可用一句话概括：
“沿着梯度的反方向，以合理步长逐步逼近目标函数的最小值。”
具体来说：

1. 梯度方向：目标函数对参数的偏导数（即梯度）指示了函数值增长最快的方向。
2. 参数更新方向：算法选择梯度的反方向（即函数值下降最快的方向）调整参数。
3. 学习率控制步长：通过设置合理的步长（学习率），在收敛速度和稳定性之间取得平衡。

---

三、关键概念

概念	定义	重要性说明
目标函数	需要最小化的函数（如损失函数 J(θ)J(θ)）	优化的目标，衡量模型预测值与真实值的差距
梯度	目标函数对参数的偏导数（∇J(θ)∇J(θ)）	指示参数调整的方向和幅度，是优化的“指南针”
学习率	参数更新时的步长（α）	过大导致震荡，过小收敛缓慢；需通过实验调整

---

四、算法步骤

梯度下降的迭代过程可拆解为以下四步：

1. 参数初始化
   随机初始化模型参数 θ（如全零、正态分布等）。
2. 梯度计算
   计算当前参数下目标函数的梯度：

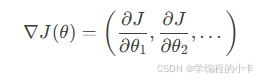
        3. 参数更新
        沿负梯度方向调整参数，学习率 α 控制步长：

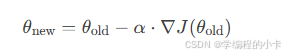
        4. 终止条件
        重复步骤2-3，直到满足以下条件之一：

•   梯度接近零（函数进入极小值点）
• 达到预设的最大迭代次数
• 损失函数变化小于阈值