数据结构——最小生成树之prime算法(与最短路径之迪杰斯特拉算法很像)

最小生成树之prime算法

***最小生成树：一个连通图的生成树中，所有边的权值加起来最小的生成树；称为最小生成树；
【简介】：Prime算法可在加权连通图里搜索最小生成树。即：所有边的权值之和为最小。
Prime算法是图论中求最小生成树的一种算法，与之类似的算法还有Kruskal算法；
区别：

Prime算法适合边多定点少的图；
Dijkstra算法适合边少定点多的图；

1.1 存图方式

要求最小生成树，当然首先要把图存进一个东西中，这样才能图对进行搜索操作。
1.邻接矩阵

存图思想：用一个矩阵来记录一个图，矩阵第 i 行第 j 列的值就表示顶点 i 到顶点 j 的权值

int matrix[MAX][MAX]={0};//邻接矩阵存储图
void init(){//初始化 min_distance[N];visited[N];数组

	 memset(visited,0,sizeof(visited));
	 for(int i=1;i<=nodeNum;i++){
	 	for(int j=1;j<nodeNum;j++){
	 		if(i == j)
			 	matrix[i][j]=0;
			else
				matrix[i][j]=INF;		 
		 }
	 } 
	
}
	init(); 
	for(int i=1;i<=nodeNum;i++){
		for(int j=1;j<=nodeNum;j++){
			cin>>matrix[i][j];
		}
	}

1.2 Prime算法分解

1.2.1 用到的数组

我写的这个Prime算法存图用的是邻接矩阵。
int min_distance[MAX]; //记录该结点到生成树的最短路径
难点在于理解min_distance数组为每个结点到生成树的最短路径

int  min_distance[MAX];     //记录该结点到生成树的最短路径 
bool visited[MAX];		//标记数组，标记该结点是否纳入集合，即该结点是否访问过；false 没有被访问 

1.2.2 初始化

初始化：自己与自己的距离为0，自己与别的结点的距离初始化为无穷大，即，表示不连通；
将所有的结点都标记为为访问，我这用false表示未访问，true表示已访问；

void init(){//初始化 min_distance[N];visited[N];数组

	 memset(visited,0,sizeof(visited));
	 for(int i=1;i<=nodeNum;i++){
	 	for(int j=1;j<nodeNum;j++){
	 		if(i == j)
			 	matrix[i][j]=0;
			else
				matrix[i][j]=INF;		 
		 }
	 } 
	
}

1.2.3 Prime算法主体

传入一个节点，当然，传入的这个节点是随意的。将这个点到其他点的距离存入min_distance数组，并将传入的这个点标记为已访问。
然后找出从start（传入的那个点）出发的路径中的最短的一个路径；并将它到达的那个点记性并标记。然后更新min_distance数组（重点）：如果该结点没有被访问过，且点距离当前点的距离更近，就执行更新；最后min_distance数组中就是最小生成树的最短路径的集合；对其求和，即是最小生成树的最短路径；
代码实现：

int prime(int start){
//start是任意一个开始结点，此节点随意；将st看做最小生成树的根节点
//开始结点的处理 
	 int i;
	for(i=1;i<=nodeNum;i++){
		if(matrix[start][i]!=INF){//这两个点之间有路径
			father[i]=start; 			
		}
		min_distance[i]=matrix[start][i];//记录起始结点到其他结点的最短路径 
	}
	visited[start]=true;//标记开始节点已经被访问
	
	
//其余结点的处理		
	while(1){
		int index=-1;//记录点的下标
		int min=INF;//标记访问到的两点之间距离的(边)最小值
		for(i=1;i<=nodeNum;i++){
			if(visited[i]==false&&min_distance[i]<min){
				min=min_distance[i];
				index=i;
			}
		}
		if(index==-1){
			break;//所有的节点都已经访问了 
		}
		//任然有节点还没有访问了
			visited[index]=true;//将刚才找到的最近的点加入到最小生成树中
			for(int i=1;i<=nodeNum;i++){//将index(新结点)可以访问到的点，重新更新一下距离
				if(visited[i]==false&&matrix[index][i]<min_distance[i]){
					//当加入新结点(index)之后，达到c(另外一个结点)的距离变小了
					min_distance[i]=matrix[index][i];
 					father[i]=index;
					} 
			}	 
	}
	for(int i=1;i<=nodeNum;i++){
		ans+=min_distance[i];
	} 
	return ans;
}

prime算法与迪杰斯特拉算法的比较很相似
仅在min_distance数组的变化上不同

if(visited[i]==false&&matrix[index][i]<min_distance[i]){
					//当加入新结点(index)之后，达到c(另外一个结点)的距离变小了
					min_distance[i]=matrix[index][i];
 					father[i]=index;
					} 

for(int i=0;i<nodeNum;i++){//添加index结点之后更新到达还未访问的点的路径长度 
			if(visited[i]==false && matrix[index][i]+min<min_distance[i]){
				min_distance[i]=matrix[index][i]+min;
			}
		} 

prime算法的代码实现：

#include<iostream>
#include<cstring>
#include<vector>
#define INF 0x3f3f3f3f//表示该两点之间没有路，距离无穷远
#define MAX 1000//最多有1000个点 
using namespace std;
int matrix[MAX][MAX]={0};//邻接矩阵存储图
int  min_distance[MAX];     //记录该结点到生成树的最短路径 
bool visited[MAX];		//标记数组，标记该结点是否纳入集合，即该结点是否访问过；false 没有被访问 
int ans=0;//返回最短路径 
int nodeNum=0;//顶点的个数 
int father[MAX];//记录父亲结点的，用于找到根节点 
void init(){//初始化 min_distance[N];visited[N];数组

	 memset(visited,0,sizeof(visited));
	 for(int i=1;i<=nodeNum;i++){
	 	for(int j=1;j<nodeNum;j++){
	 		if(i == j)
			 	matrix[i][j]=0;
			else
				matrix[i][j]=INF;		 
		 }
	 } 
	
}
int prime(int start){
//start是任意一个开始结点，此节点随意；将st看做最小生成树的根节点
//开始结点的处理 
	 int i;
	for(i=1;i<=nodeNum;i++){
		if(matrix[start][i]!=INF){//这两个点之间有路径
			father[i]=start; 			
		}
		min_distance[i]=matrix[start][i];//记录起始结点到其他结点的最短路径 
	}
	visited[start]=true;//标记开始节点已经被访问
	
	
//其余结点的处理		
	while(1){
		int index=-1;//记录点的下标
		int min=INF;//标记访问到的两点之间距离的(边)最小值
		for(i=1;i<=nodeNum;i++){
			if(visited[i]==false&&min_distance[i]<min){
				min=min_distance[i];
				index=i;
			}
		}
		if(index==-1){
			break;//所有的节点都已经访问了 
		}
		//任然有节点还没有访问了
			visited[index]=true;//将刚才找到的最近的点加入到最小生成树中
			for(int i=1;i<=nodeNum;i++){//将index(新结点)可以访问到的点，重新更新一下距离
				if(visited[i]==false&&matrix[index][i]<min_distance[i]){
					//当加入新结点(index)之后，达到c(另外一个结点)的距离变小了
					min_distance[i]=matrix[index][i];
 					father[i]=index;
					} 
		 
			
			}	 
		
		
	
	}
	for(int i=1;i<=nodeNum;i++){
		ans+=min_distance[i];
	} 
	return ans;
}


void parent(){//寻找根节点 
	for(int i=1;i<=nodeNum;i++){
		if(father[i]==i)
			cout<<i<<"结点是根节点！"<<endl;
		else{
			cout << i << "的父亲结点是：" << father[i] << endl;
		} 
	}
}
int main()
{
	cin>>nodeNum;
	//存储结点是从1开始的
		init(); 
	for(int i=1;i<=nodeNum;i++){
		for(int j=1;j<=nodeNum;j++){
			cin>>matrix[i][j];
		}
	}

	cout<<prime(1)<<endl;
	parent();
	return 0;

}

AcWing 858. Prim算法求最小生成树

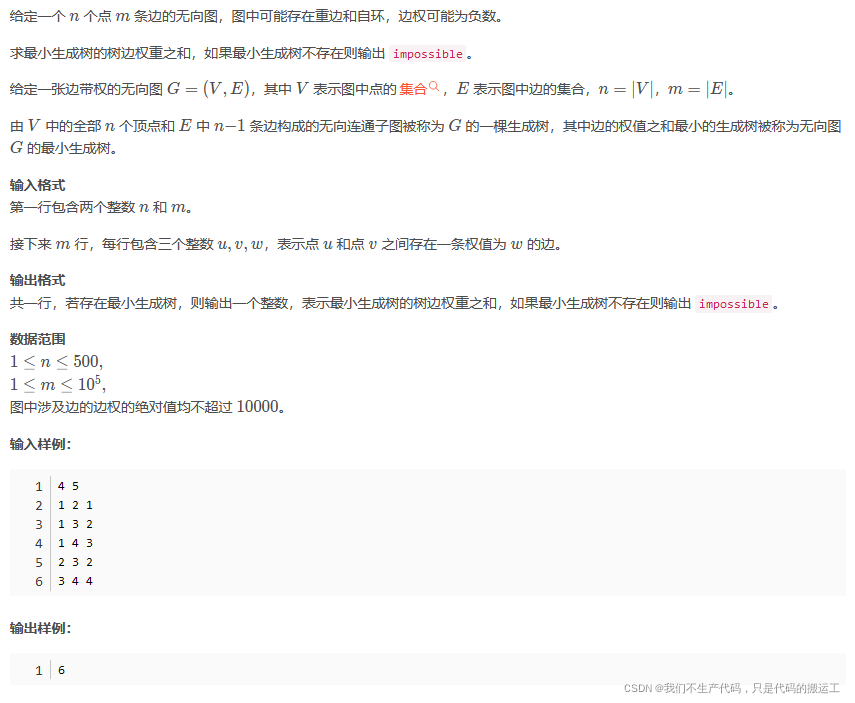
首先以一个结点作为最小生成树的初始结点，然后以迭代的方式找出最小生成树中各结点权重最小的边，并加到最小生成树中。（加入之后如果产生回路了就要跳过这条边，选择下一个结点）当所有的结点都加入到最小生成树中后，就找出了这个连通图的最小生成树～

y总的prim算法

#include<bits/stdc++.h>
using namespace std;
const int N=510;
const int INF=0x3f3f3f3f;
int n,m;      // n表示点数
int g[N][N];        // 邻接矩阵，存储所有边
int dist[N];        // 存储其他点到当前最小生成树的距离
bool st[N];     // 存储每个点是否已经在生成树中


// 如果图不连通，则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
    memset(dist, INF, sizeof(dist));

    int res = 0;//计算最小生成树的权值
    for (int i = 0; i < n; i ++ )
    {
        int index = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (index == -1 || dist[index] > dist[j]))
                index = j;

        if (i && dist[index] == INF) return INF;//如果距离集合S的距离为INF则说明不能构成生成树

        if (i) res += dist[index];//先将选择的边计入S集合中，防止出现自环等产生错误结果
        st[index] = true;

        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[index][j]);//更新到集合S的距离
    }

    return res;
}
int main(){
    cin>>n>>m;
    memset(g,INF,sizeof (g));
    memset(dist,INF,sizeof (dist));
    while(m--){
        int a,b,c; 
		cin>>a>>b>>c;
        g[a][b]=g[b][a]=min(g[a][b],c);
    }
    int res=prim();
    if(res==INF) 
		cout<<"impossible"<<endl;
    else 
		cout<<res<<endl;
    return 0;
}