问题描述
将图以邻接矩阵或邻接表存储,实现Dijkstra算法。
算法设计
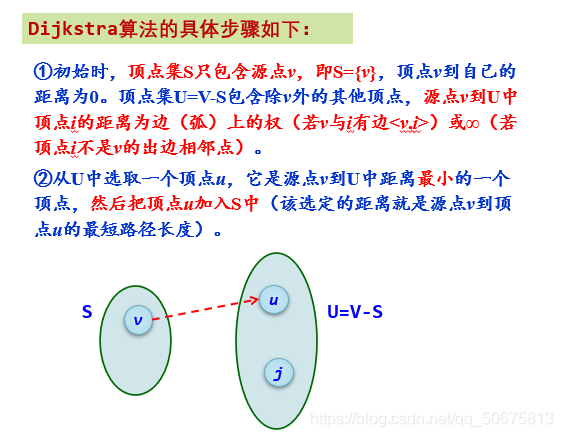
迪杰斯特拉算法:
1.假设用带权的邻接矩阵arc,来表示带权有向图,arc[i][j],表示弧<vi,vj>上的权值。若<vi,vj>不存在,则置arc[i][j]为无穷。
S为已找到从v出发的最短路径的终点的集合,它的初始状态为空集。那么,从v出发到图上其余各顶点可能达到的最短路径长度的初值为:
D[j]=arcs[LocateVex(G,v)][i] vi∈V
2.选择vj,使得 D[j]=Min{D[i]|vi∈V-S}
vj就是当前求得的一条从v出发的最短路径的终点。令S=S∪{j}
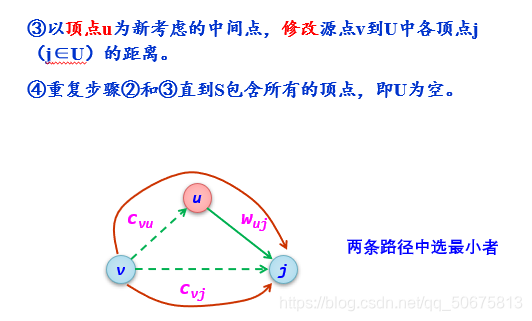
3.修改从v出发到集合V-S上任一顶点vk可达的最短路径长度。如果
D[j]+arcs[j][k]<D[k] 则修改D[k]为D[k]=D[j]+arcs[j][k]
4.重复操作2,3共n-1次。
由此求得从v到图上其余各顶点的最短路径是依路径长度递增的序列。
#include<stdio.h>
#include<string.h>
#define INF 32767
#define MAXVEX 30
int dist[MAXVEX]; //建立dist数组
int path[MAXVEX]; //建立path数组
int S[MAXVEX]; //建立S数组
typedef char VertexType;
typedef struct graph
{
int n,e;
VertexType vexs[MAXVEX];
int edges[MAXVEX][MAXVEX];
}MGraph;
void CreateMGraph(MGraph &G)
{
int n,e;
int value;
char temp_i;
char temp_j;
printf("请输入图的顶点数和边数(以空格分隔):");
scanf("%d%d",&n,&e);
G.n=n;G.e=e;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(i==j)
G.edges[i][j]=0;
else
G.edges[i][j]=32767;
}
}
printf("输入顶点信息:");
for(int j=0;j<G.n;j++)
{
getchar();
scanf("%c",&G.vexs[j]);
}
int temp_number_i;
int temp_number_j;
printf("请输入每条边的权值:\n");
for(int j=0;j<e;j++)
{
getchar();
scanf("%c %c %d",&temp_i,&temp_j,&value);
for(int i=0;i<n;i++)
{
if(G.vexs[i]==temp_i)
temp_number_i=i;
if(G.vexs[i]==temp_j)
temp_number_j=i;
}
G.edges[temp_number_i][temp_number_j]=value;
}
}
void DispMGraph(MGraph &G)
{
printf("输出顶点信息:\n");
for(int i=0;i<G.n;i++)
{
printf("%c",G.vexs[i]);
}
printf("\n输出邻接矩阵:\n");
printf("\t");
for(int i=0;i<G.n;i++)
printf("%8c",G.vexs[i]);
for(int i=0;i<G.n;i++)
{
printf("\n%8c",G.vexs[i]);
for(int j=0;j<G.n;j++)
{
if(G.edges[i][j]==32767)
//两点之间无连接时权值为默认的32767,
// 在无向图中一般用"0"表示,在有向图中一般用"∞",
// 这里为了方便统一输出 "∞"
printf("%8s", "∞");
else
printf("%8d",G.edges[i][j]);
}
printf("\n");
}
}
void Dijkstra(MGraph g, int v)
{
//求从v到其他顶点的最短路径
int mindis,i,j,u=0;
for (i=0;i<g.n;i++)
{ dist[i]=g.edges[v][i]; //距离初始化
S[i]=0; //S[]置空
if (g.edges[v][i]<INF) //路径初始化
path[i]=v; //v→i有边时,置i前一顶点为v
else //v→i没边时,置i前一顶点为-1
path[i]=-1;
}
S[v]=1; //源点编号v放入S中
for (i=0;i<g.n-1;i++) //循环向S中添加n-1个顶点
{ mindis=INF; //mindis置最小长度初值
for (j=0;j<g.n;j++) //选取不在S中且有最小距离顶点u
if (S[j]==0 && dist[j]<mindis)
{ u=j;
mindis=dist[j];
}
S[u]=1; //顶点u加入S中
for (j=0;j<g.n;j++) //修改不在s中的顶点的距离
if (S[j]==0)
if (g.edges[u][j]<INF
&& dist[u]+g.edges[u][j]<dist[j])
{ dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
}
void Print(MGraph G,int v)
{
printf("\n");
for(int i=0;i<G.n;i++){
if(i!=v && dist[i]!=INF){
printf("%c到%c的最短距离为:%d\n",G.vexs[v],G.vexs[i],dist[i]);
}else if(dist[i]==INF){
printf("%c与%c之间无路径!\n",G.vexs[v],G.vexs[i]);
}
}
printf("\n");
}
/*------------------输出从顶点v出发的所有最短路径-------------------*/
static void Dispath(MGraph g, int v)
{
int i, j, k;
int apath[MAXVEX], d; //存放一条最短路径(逆向)及其顶点个数
//循环输出从顶点v到i的路径
for(i = 0; i < g.n; i++)
{
if(S[i] == 1 && i != v)
{
printf("从顶点%c到顶点%c的路径长度为:%d\t路径为:", g.vexs[v], g.vexs[i], dist[i]);
d = 0; apath[d] = i; //添加路径上的终点
k = path[i];
if(k == -1) //没有路径的情况
printf("无路径\n");
else //存在路径时输出该路径
{
while(k != v)
{
d++;
apath[d] = k;
k = path[k];
}
d++; apath[d] = v; //添加路径上的起点
printf("%c ", g.vexs[apath[d]]); //先输出起点
for(j = d - 1; j >= 0; j--) //再输出其余顶点
printf(" %c ", g.vexs[apath[j]]);
printf("\n");
}
}
}
}
int main()
{
MGraph G;
CreateMGraph(G);
DispMGraph(G);
Dijkstra(G,0);
Print(G,0);
Dispath(G,0);
}
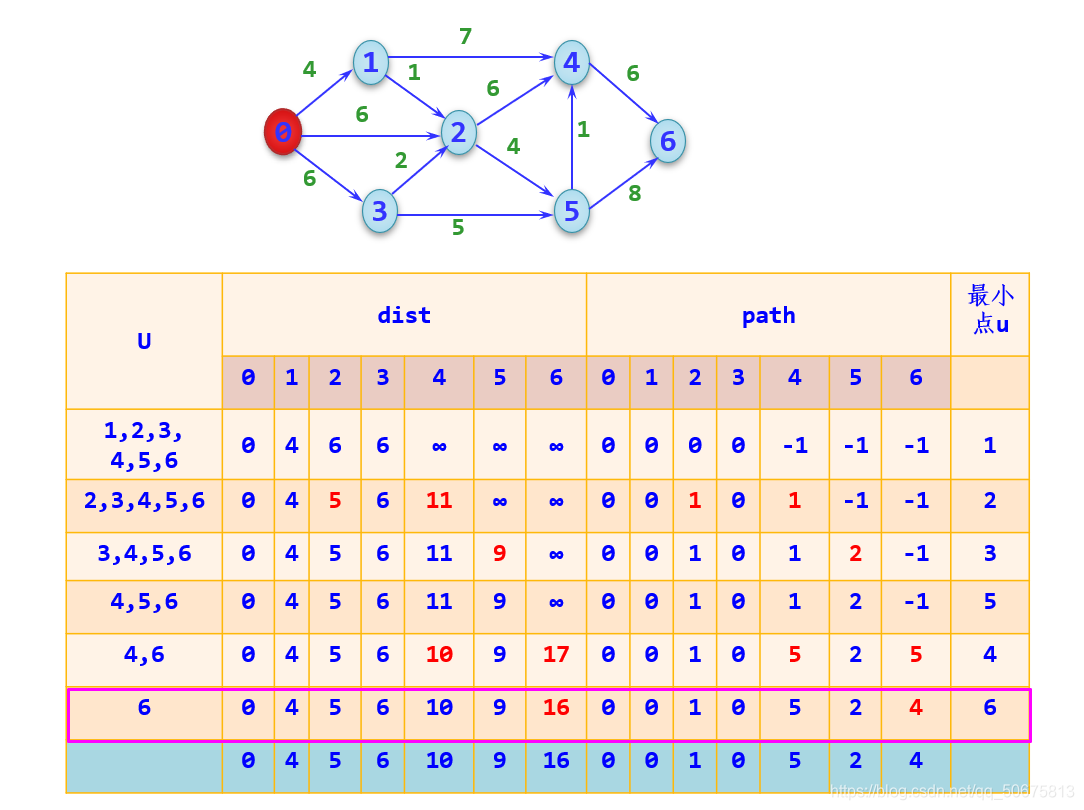
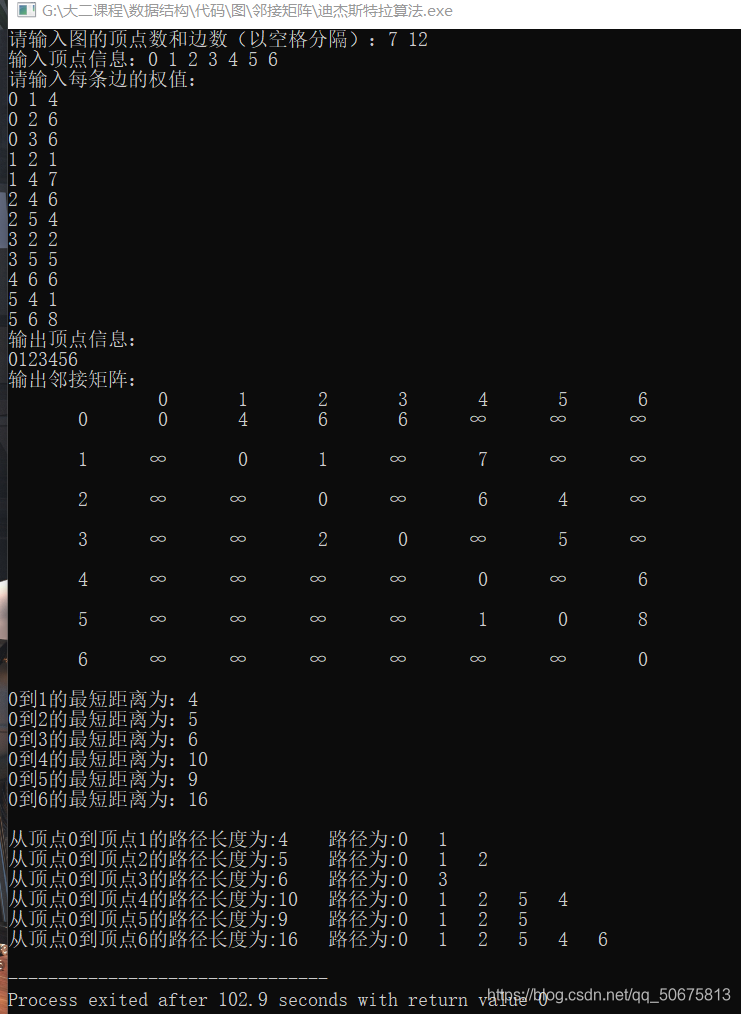





 该博客聚焦于用C语言解决图的路径问题,将图以邻接矩阵或邻接表存储,实现Dijkstra算法。详细介绍了迪杰斯特拉算法的设计,包括用带权邻接矩阵表示有向图,通过一系列步骤求得从某点到其余各顶点依路径长度递增的最短路径。
该博客聚焦于用C语言解决图的路径问题,将图以邻接矩阵或邻接表存储,实现Dijkstra算法。详细介绍了迪杰斯特拉算法的设计,包括用带权邻接矩阵表示有向图,通过一系列步骤求得从某点到其余各顶点依路径长度递增的最短路径。

















 624
624

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








