蓝桥杯：2018年第九届蓝桥杯省赛B组第七题—螺旋折线（Java实现）

螺旋折线

题目描述
如图p1.pgn所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。

例如dis(0, 1)=3, dis(-2, -1)=9

给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？

【输入格式】
X和Y

对于40%的数据，-1000 <= X, Y <= 1000
对于70%的数据，-100000 <= X， Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000

【输出格式】
输出dis(X, Y)

【输入样例】
0 1

【输出样例】
3

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

思路：
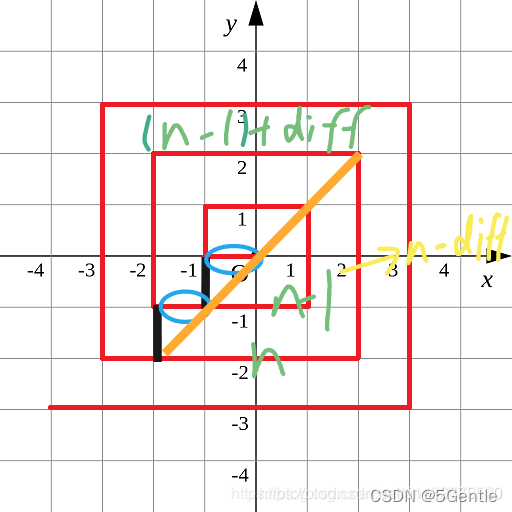
这里发现是有规律的，所以可以取巧，我们发现说是螺旋，其实将蓝圈内的线段移到黑色线段位置就是嵌套的正方形，各个层的正方形结尾坐标就是 (-1,-1)、(-2,-2)、(-3,-3)、… (-n,-n)
第一层距离（正方形周长）：8，第二层： 16， 第三层： 24
这里不难发现这里是有规律的，1x8 2x8 3x8，那就是 8x(1+2+3+…+n)，就是 8x(nx(n+1)/2) == 4n+4n^2
题目给的是坐标，怎么知道这个坐标是在第几层的呢，我们也可以发现就是坐标中绝对值的最大值，取出来计算到当前层的总距离就可以了
因为我们只能确定在第n层，在哪个位置还需要再做计算，如果直接计算该位置和（-n,-n）坐标的横纵坐标差和有些情况是不可行的，如果用当前层总距离减这个横纵坐标差和，（ x=[-n,n），y=(-n,n] ）这个范围是有问题会少减，如果用(n-1)层的总距离加横纵坐标差值和，（ x=(-n,n] ，y=[-n,n) ）这个范围的有问题会少加，但这两种情况却刚好可以将这一层的所有位置都包含到
所以我们直接把这一层分成两种情况进行处理就可以了

如图所示的螺旋折线

代码：

import java.math.BigInteger;
import java.util.Scanner;
/**
 * @author 宝哥居士
 * @Create -03-27-17:17
 */
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        // 接收输入的数据，因为数据范围 所以使用大数类型
        BigInteger x = sc.nextBigInteger();
        BigInteger y = sc.nextBigInteger();
        // 取绝对值中的较大值
        BigInteger max = x.abs().max(y.abs());
        // 声明 4 的大数类型 后面多处用到
        BigInteger four = new BigInteger("4");
        // 将最大值取反 (-max,-max)就是我们要找的我们计算的起点
        BigInteger maxXY= max.negate();
        // 根据是现在的第几层了，我们计算前面的嵌套层数距离的和
        // 我们发现各个层的距离也就是 4 x 正方形边长 8 16 24 我们发现各层的层数是 8n
        // 8取出来就是一个递增和 8*(1+2+3+...+n) 也就是 8 * (n*(n+1)/2) == 4n + 4n^2
        BigInteger sum = four.multiply(max);
        sum = sum.add(four.multiply(max.pow(2)));
        // 因为两种情况，我们还需要计算前一层的总层距离
        BigInteger pre = max.subtract(new BigInteger("1"));
        BigInteger preSum = four.multiply(pre);
        preSum = preSum.add(four.multiply(pre.pow(2)));
        // 根据(x,y) 和 (maxXY,maxXY)的距离的绝对值计算差值
        BigInteger diff = x.subtract(maxXY).abs();
        diff = diff.add(y.subtract(maxXY).abs());
        // 现在分两种情况处理 x < max && y>maxXY 的距离是前一层总和加上这个差值
        if (x.compareTo(max)==-1 && y.compareTo(maxXY) == 1){
            preSum = preSum.add(diff);
            System.out.println(preSum);
        // 其他的位置则是当前层数总和减去还没有到达该坐标的距离
        }else {
            sum = sum.subtract(diff);
            System.out.println(sum);
        }
    }
}