JS归并排序

一、基本思想

先将序列一次次分成子序列，直到子序列长度为1；再将已有序的子序列合并，得到完全有序的序列。运用了 分而治之的思想(分治法) 。

二、例子

输入数组 [ 2, 5, 3 , 10, -3, 1 , 6 , 4]；初始状态如下：

分治思想如下：
首先把数组依次折半，分成小的子数组，直到每一个子数组的长度都为1；然后合并子数组，在合并的过程中进行排序；

 

 

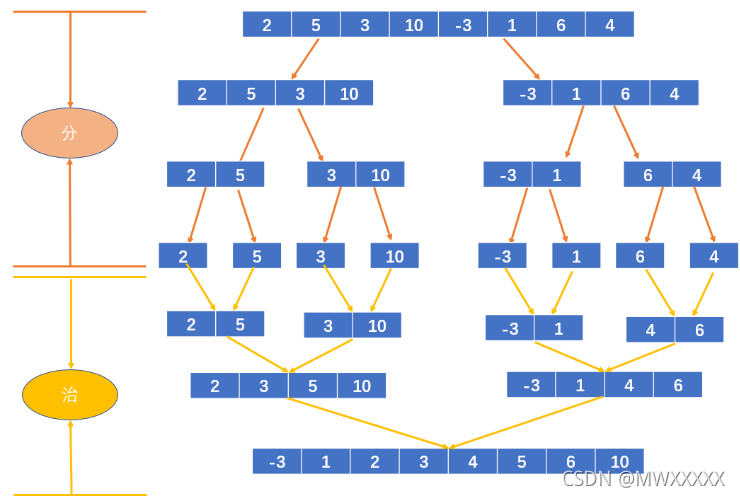
将数组分成子数组的方法比较简单，不过多介绍；

下面介绍一下合并操作,以最后一次合并为例：

下图是最后一次合并前的两个数组：

 

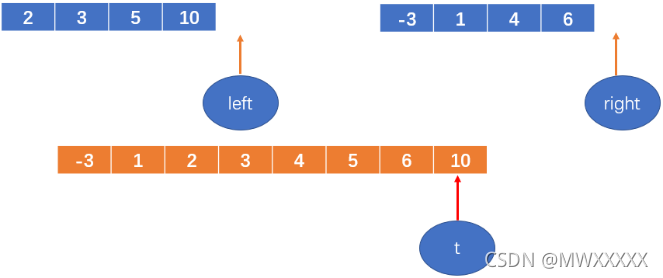
定义两个变量 left和right，分别赋值为两个数组的首元素的索引；
初始化一个数组，数组长度为原数组大小；
再定义一个变量，t，初始化为新开的数组的第一个元素的索引，即0；
如下图：

 

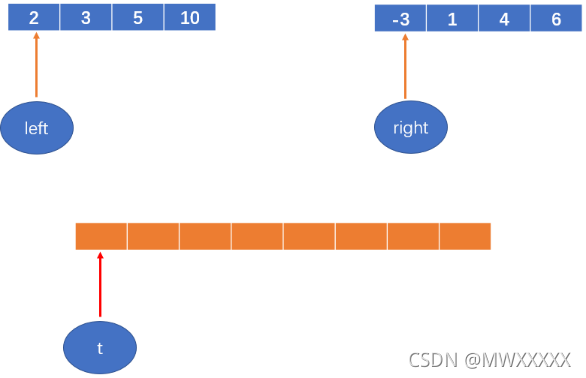
然后每次从两个数组中找相对较小的数，填到新开的数组中；

-3 < 2，将-3填到数组中，right++;

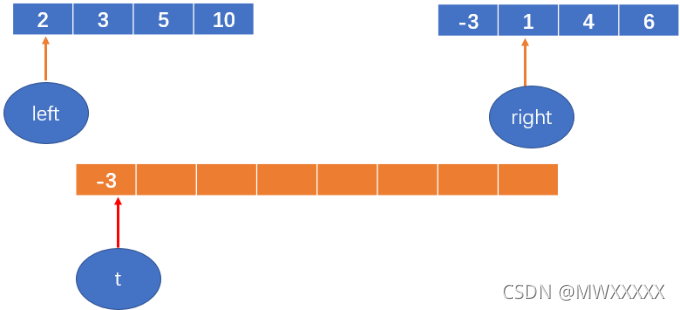
 t++;

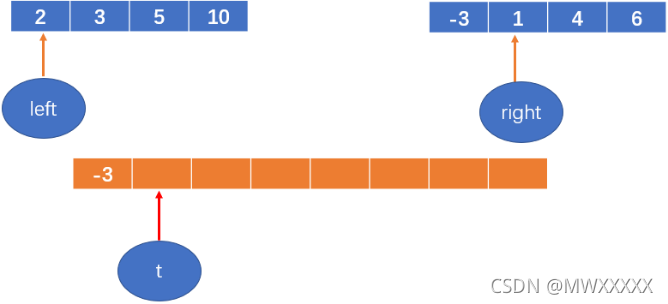
 1< 2，将1填到数组中，right++;

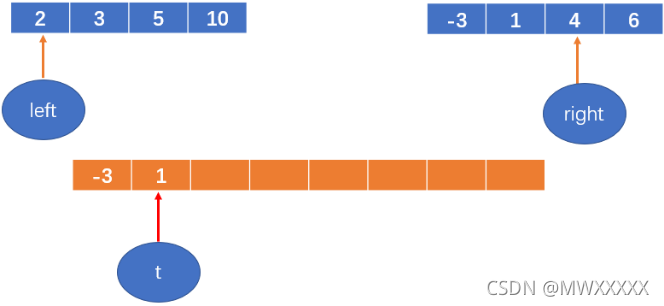
 t++;

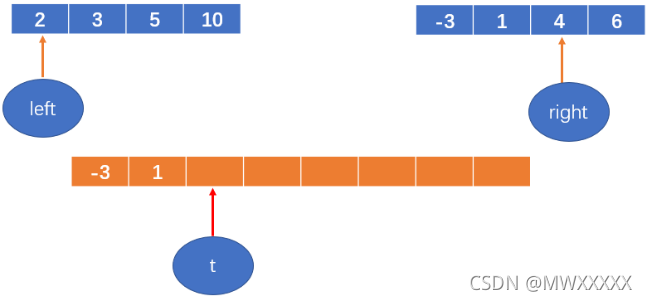
 2 < 4，将2填到数组中，left++;

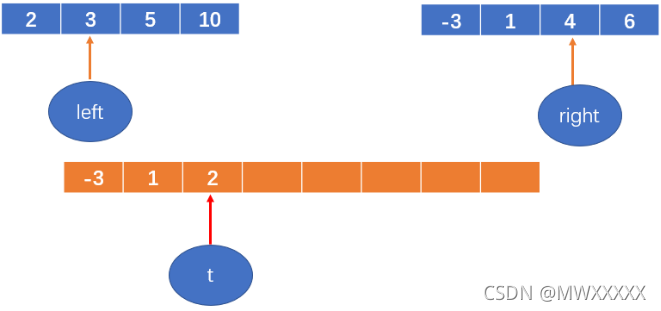
 t++；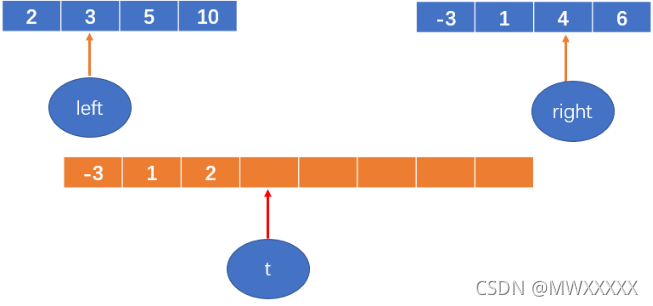

 

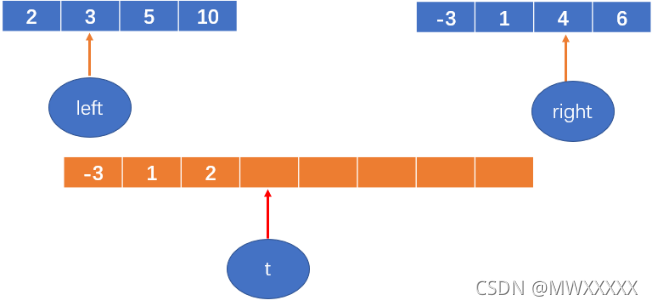
 3 < 4，将3填到数组中，left++;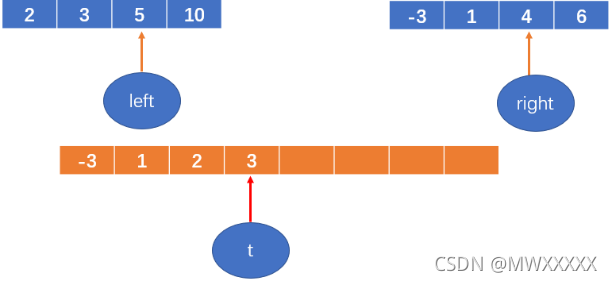

 t++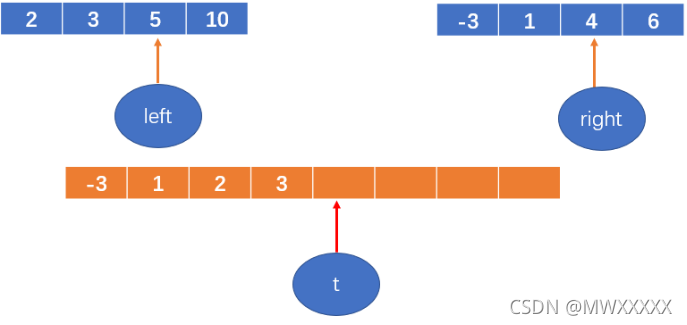

 4 < 5，将4填到数组中，right++;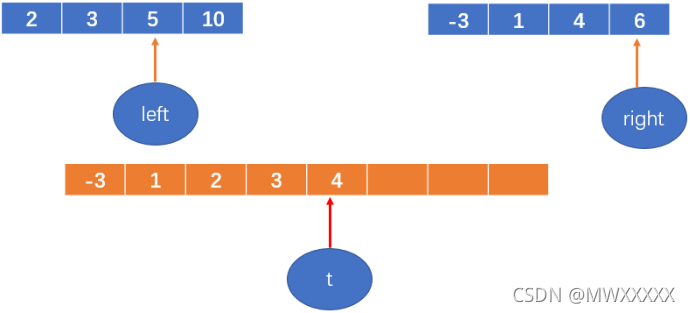

 t++

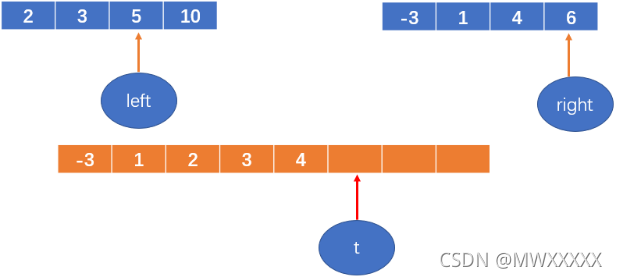
 5 < 6，将5填到数组中，left++;

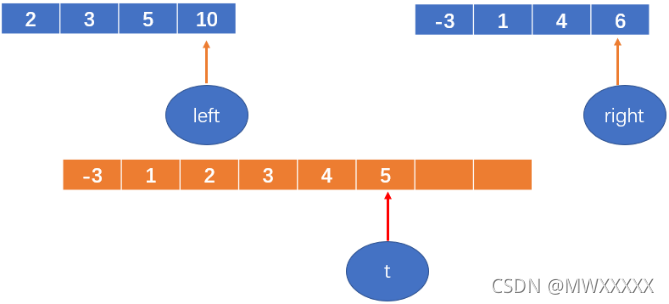
6 < 10，将6填到数组中，right++后越界

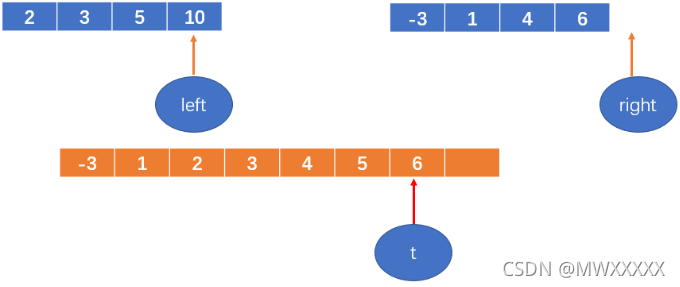
 t++

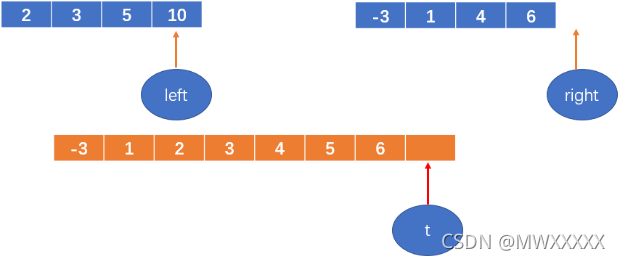
 再把剩余的数加到数组里，直到子数组中的数都填过来；

 三、JavaScript代码实现

*
 合并方法：
   @param arr 待排序数组
   @param left 左边序列的初始索引
   @param mid 中间索引(用来判断左边序列何时结束：到mid结束,右边序列何时开始：即mid+1)
   @param right 右边数组结束的索引
   @param temp 临时存储的数组
*/
function merge(arr,left,mid,right,temp){
    var i = left; //左边有序序列的初始索引
    var j = mid+1; //右边有序序列的初始索引
    var t = 0; //指向临时数组的当前索引
    //将两边数组元素进行比较,一次填进临时数组,直到将一边填完
    while(i<=mid && j<=right){
        if(arr[i]<=arr[j]){ //选择较小的添加进去
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }else{
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }
    }
    /*
      把有剩余数据的数组全部填充到数组
    */
   while(i<=mid){
       temp[t]= arr[i];
       t += 1;
       i += 1;
   }
   while(j<=right){
    temp[t]= arr[j];
    t += 1;
    j += 1;
   }
   //将temp数组的元素拷贝到arr
   t = 0;
   var k = left;
   while(k<=right){
       arr[k] = temp[t];
       t += 1;
       k += 1;
   }
}
/*
  归并(分+治)方法
*/
function mergeSort(arr,left,right,temp){
    if(left<right){
        var mid = parseInt((left+right)/2);//中间索引
        mergeSort(arr,left,mid,temp);//左边递归分解
        mergeSort(arr,mid+1,right,temp);//右边递归分解
        merge(arr,left,mid,right,temp);//合并
    }
}
var arr = [2,5,3,10,-3,1,6,4];
var temp = new Array(arr.length);
console.log("排序前的数组：",arr);
mergeSort(arr,0,arr.length-1,temp);
console.log("排序后的数组：",arr);

四、时间复杂度、

归并排序的是按照分层进行比较的，会分成log2n层；

而每一层的比较次数为O(n)；

所以时间复杂度求得O(nlogn)。

五、稳定性

在交换元素时，可以限定元素相等时不移动，所以归并排序是可以稳定的。