数据结构与算法 python语言实现第4章课后习题

R-4.1 对于一个含有n个元素的序列S，描述一个递归算法查找其最大值。所给出的递归算法时间复杂度和空间复杂度各是多少?
python中三目运算符的写法
x if(x>y)) else y

def max(data,n):
    if n==1:
        return data[0]
    else:
        m=max(data,n-1)
        return data[n-1] if(data[n-1]>m) else m

共执行n次递归调用，因为它花费恒定的时间执行非递归的部分 所以时间复杂度是O(n)
空间复杂度也是O(n)

R-4.2使用在代码段4-11中实现的传统函数，绘制出power(2,5)函数计算的递归跟踪

R-4.3如代码段4-12中实现的函数所示，使用重复平方算法,绘制出power(2,18)函数计算的递归跟踪

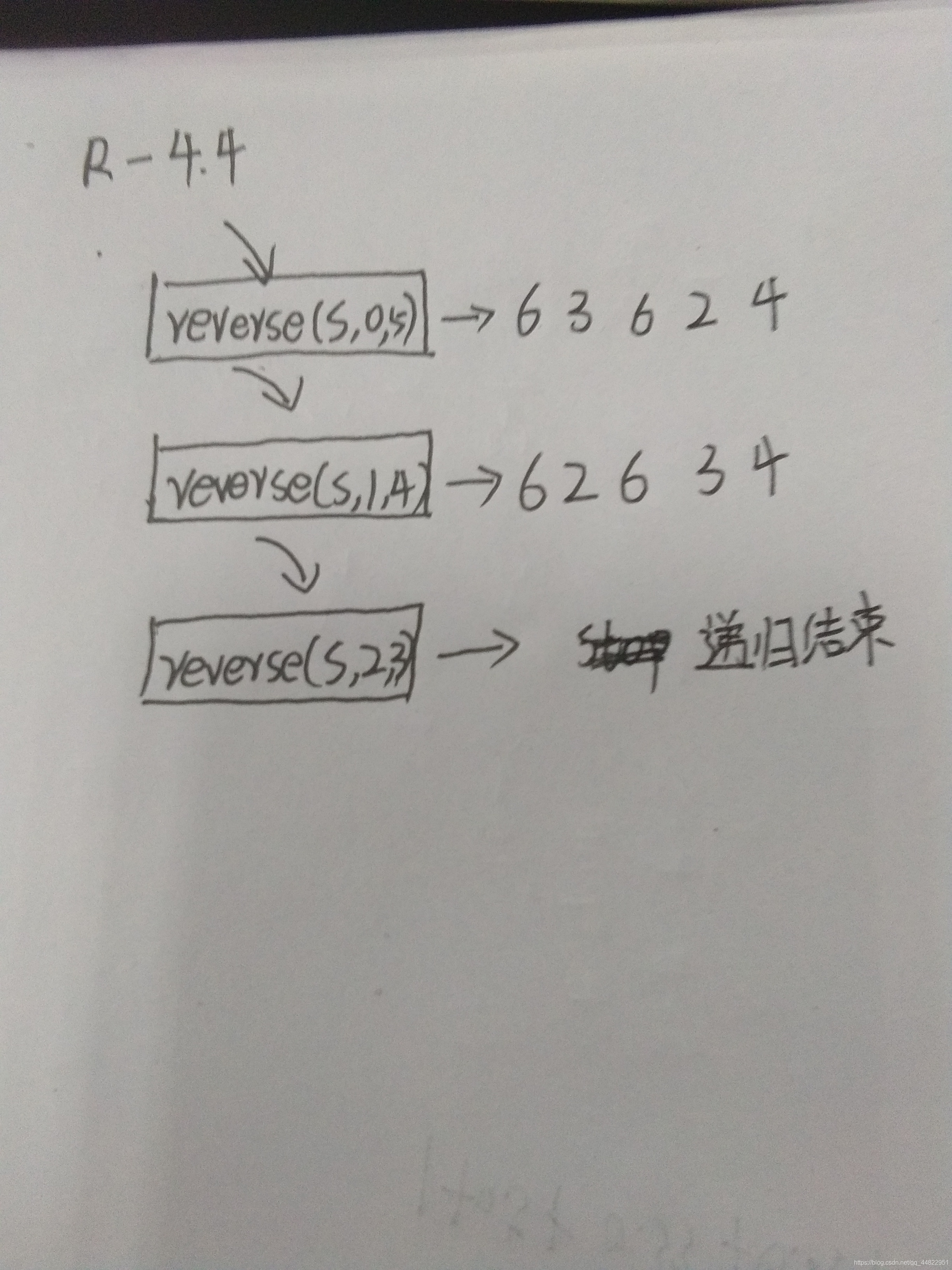
R-4.4 绘制函数reverse(S,0,5)（代码段4-10)执行的递归追踪,其中S=[4,3,6,2,6]

R-4.6 写一个递归函数,用于计算第n个调和数，其中 Hn=1+1/2+1/3+…+1/n

def harmonic(n):
    if n==1:
        return 1
    else:
        return harmonic(n-1)+1/n
print(harmonic(6))

R-4.7 写一个递归函数,它可以把一串数字转换成对应的整数

def tonum(data,m,n):
    if m==len(data)-1:
        return data[m]
    else:
        return data[m]*pow(10,n-1)+tonum(data,m+1,n-1)
data=[1,2,3,4,5]
print(tonum(data,0,len(data)))

R-4.8Isabel用一种有趣的方法来计算一个含有n个整数的序列A的所有元素之和，其中n是2的幂.她创建一个新的序列B，其大小是序列A的一半并且设置
B[i]=A[2i]+A[2i+1] (i=0,1,…,(n/2)-1)。如果B的大小为1,那么输出B[0]；否则，用B取代A，并且重复这个过程。那么她的这个算法的时间复杂度是多少？

def sum(A):
    B=[]
    if len(A)==1:
        return A[0]
    else:
        for i in range(0,len(A)//2):
            B.append(A[2*i]+A[2*i+1])
        A=B
        return sum(A)
A=[1,2,3,4,5,6,7,8]
print(sum(A))
B=[1,2,3,4]
print(sum(B))

时间复杂度 O(logn)

C-4.9写一个简短的递归Python函数，用于在不使用任何循环的条件下查找一个序列中的最小值和最大值

def maxmin(data,n):
    if n == 1:
        return data[0],data[0]
    else:
        x ,y= maxmin(data, n - 1)
        return data[n - 1] if (data[n - 1] > x) else x, data[n - 1] if (data[n - 1] <y) else y
data=[1,2,3,4,5,6,7,8,9,10]
m,n=maxmin(data,10)
print(m,n)

C-4.10在只使用加法和整数除法的情况下,描述一个递归算法,来计算以2为底的n的对数的整数部分
让n除以2 循环进行 循环执行了几次说明整数部分是多少

def num(n):
    if(n==1):
        return 0;
    else:
        n=n//2
        return num(n)+1
print(num(32))

C-4.11 描述一个有效的递归函数来求解元素的唯一性问题,在不使用排序的最坏的情况下运行时间最多是O(n^2)
C-4.12在只使用加法和减法的情况下,给出一个递归算法,来计算两个正整数m和n的乘积
mn 就是对m做n次加法 如m2=m+m

def multiply(m,n):
    if n==0:
        return 0
    else:
        return m+multiply(m,n-1)
print(multiply(54,45))

C-4.15编写一个递归函数,该函数将输出一个含有n个元素的集合的所有子集（没有任何重复的子集)

def subset(data,p,q,flag):
    if p==q:
        for i in range(0,q):
            if flag[i]:
                print(data[i],end="")
        print("\n")
        return
    flag[p]=0
    subset(data,p+1,q,flag)
    flag[p] = 1
    subset(data,p+1,q,flag)
data=[1,2,3,4]
flag=[0,0,0,0]
subset(data,0,4,flag)

C-4.16编写一个简短的递归python函数,它接收一个字符串s并输出其逆置字符串

def reverse(strs):
   if len(strs)==0:
       return ' '
   else:
       return reverse(strs[1:])+strs[0]
strs="123456789"
print(reverse(strs))

C-4.17编写一个简短的递归python函数,确定一个字符串s是否是一个回文字符串

def ishuiwen(str,m,n):
    if m<n-1:
        if str[m]!=str[n-1]:
            return False
        else:
            return ishuiwen(str,m+1,n-1)
    return True
str="abccbaed"
print(ishuiwen(str,0,len(str)))

C-4.19编写一个简短的递归python函数,用于重新排列一个整数值序列,使得所有偶数值出现在所有奇数值的前面

def order(data,i,j):
    if i<j:
        while i<j and data[i]%2==0:
            i=i+1
        while i<j and data[j]%2==1:
            j=j-1
        temp=data[i]
        data[i]=data[j]
        data[j]=temp
        order(data,i+1,j-1)
data=[1,3,5,7,2,4,6,8]
order(data,0,7)
print(data)

C-4.20 给定一个未排序的整数序列S和整数k,描述一个递归算法,用于对S中的元素重新排序,使得所有小于等于k的元素在所有大于k的元素之前.在这个含有n个值的序列中,算法的时间复杂度是多少

C-4.21假设给出一个含有n个元素的序列S，这个序列是包含不同元素的升序序列。给定一个数k,描述一个递归算法找到S中总和为k的两个整数（如果这样的一对整数存在).算法的时间复杂度是多少

C-4.22 从代码段4-12使用重复平方的power函数的版本中,实现一个非递归实例

P-4.16编写函数解决汉诺塔问题

def move(n,x,y):
    print("从"+x+"移动到"+y)
def Hanoi(x,y,z,n):
    if n==1:
        move(n,x,z)
    else:
        Hanoi(x,z,y,n-1)
        move(n,x,z)
        Hanoi(y,x,z,n-1)
Hanoi('a','b','c',4)