汉诺塔

古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小 不等，大的在下，小的在上（如图）。有一个和尚想把这64个盘子从A座移 到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子 始终保持大盘在下，小盘在上。在移动过程中可以利用B座，要求输出移动 的步骤。

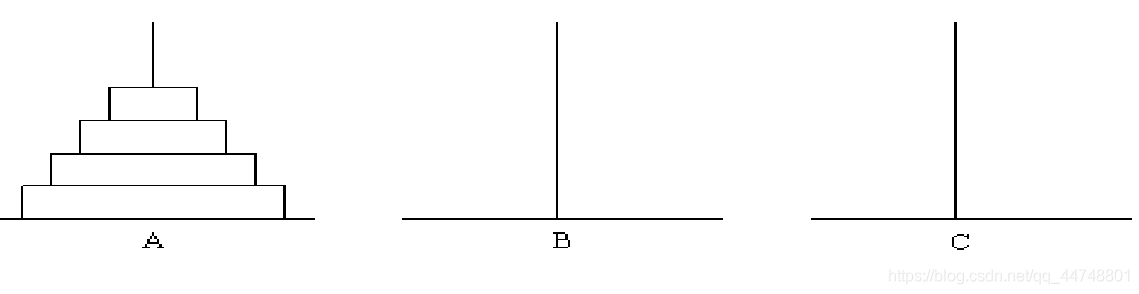
我们的办法是，先将前面的n-1个盘子通过C放到B然后将第N个放到C然后在将B上的通过A放到C。

#include <iostream>
using namespace std;
void Hanoi(int n, char src,char mid,char dest,int src_n) //将src座上的n个盘子，以mid座为中转，移动到dest座 
//src座上最上方盘子编号是 src_n 
{ 
	if( n == 1) 
	{  //只需移动一个盘子 
		cout << src_n << ":" << src << "->" << dest << endl; //直接将盘子从src移动到dest即可 
		return ; 
	} 
	Hanoi(n-1,src,dest,mid,src_n); //先将n-1个盘子从src移动到mid 
	cout << src_n + n - 1 << ":" << src << "->" << dest << endl; //再将一个盘子从src移动到dest 
	Hanoi(n-1,mid,src,dest,src_n); //最后将n-1个盘子从mid移动到dest 
	return ; 
}
int main() {
	char a, b, c; 
	int n; 
	cin >> n >> a >> b >> c; //输入盘子数目 
	Hanoi(n,a,b,c,1); 
	return 0; 
}