顺序表的实现（C语言）

线性表

• 线性表（linear list）是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串...
• 线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。

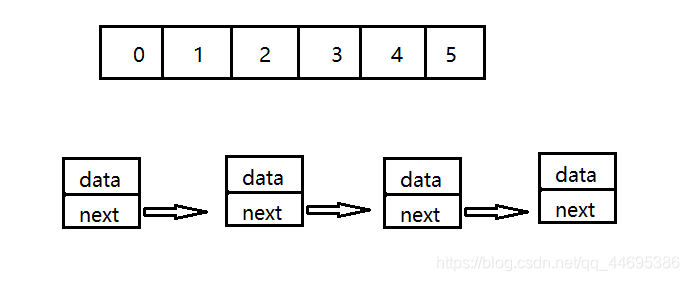
顺序表

顺序表 是指用一组地址连续的存储单元依次存储线性表中的各个元素、使得线性表中在逻辑结构上相邻的数据元素存储在相邻的物理存储单元中

静态顺序表的实现

// 静态顺序表的定义
#define MaxSize 50    //定义顺序表的最大长度
typedef int ElemType; //定义元素的存储类型

typedef struct{
	ElemType data[MaxSize];  //顺序表的元素
	int length;              //顺序表的长度
}SeqList;                    //顺序表的类型定义

// 静态顺序表的基本操作
// 静态顺序表的初始化
void SeqListInit(SeqList& L)
{
	for (int i = 0; i < MaxSize; i++)
		L.data[i] = 0;    //将所有数据元素设置为默认初始值,
	//如果没有设置数据元素的默认值，内存中会有遗留的脏数据
	L.length = 0;         //顺序表初始长度为0
}

// 求顺序表的长度
int Length(SeqList& L)
{
	return L.length;
}

// 打印顺序表
void SeqListPrint(SeqList& L)
{
	for (int i = 0; i < L.length; i++)
		printf("%d->", L.data[i]);
	printf("\n");
}

// 插入操作（按位序插入）
// 平均时间复杂度O(N)
bool SeqListInsert(SeqList& L, int i, ElemType e)
{
	if (i<1 || i>L.length)    //判断i的位置是否有效
		return false;
	if (L.length >= MaxSize)  //当前存储空间已满，不能插入
		return false;
	for (int j = L.length; j >= i; j--)  //将第i个元素及之后的元素后移
		L.data[j] = L.data[j - 1];
	L.data[i - 1] = e;                   //在位置i处放入e
	L.length++;                          //线性表的长度加1
	return true;
}

// 删除操作
// 平均时间复杂度O(N)
bool SeqListDelete(SeqList& L, int i, ElemType &e)
{
	if (i < 1 || i>L.length) //判断i的范围是否有效
		return false;
	e = L.data[i - 1];                   //将被删除的元素赋值给e
	for (int j = i; j < L.length; j++)   //将第i个位置后的元素前移
		L.data[j - 1] = L.data[j];
	L.length--;                          //线性表长度减1
	return true;
}

// 按值查找（顺序查找）
// 平均时间复杂度0(N)
int LocateElem(SeqList L, ElemType e)
{
	for (int i = 0; i < L.length; i++)
	{
		if (L.data[i] == e)    //基本数据类型(int,float,char,double)可以直接用运算符==比较，结构体类型不可以拿==比较
			return i + 1;      //下标为i的元素值等于e,返回其位序i+1
	}
	return 0;                  //退出循环，说明查找失败
}

// 按位序查找
// 时间复杂度O(1)
SeqList& GetElem(SeqList& L, ElemType i)
{
	return L.data[i - 1];
}

// 判空操作
bool Empty(SeqList& L)
{
	return L.length == 0;
}

// 销毁操作
void Destroy(SeqList& L)
{
	L->length == 0;  //销毁操作只需将有效个数设置为0
}

动态顺序表的实现

// 动态顺序表的定义
typedef int ElemType;
#define InitSize 10        //表长度的初始定义
typedef struct{
	ElemType *data;         //指示动态分配数组的指针
	int MaxSize;            //顺序表的最大容量
	int length;             //顺序表的当前元素个数
}SeqList;

// 动态顺序表的初始化
void SeqListInit(SeqList& L)
{
	//用malloc函数申请一片连续的存储空间
	L.data = (int*)malloc(InitSize*(int));
	L.length = 0;
	L.MaxSize = InitSize;
}

// 增加动态顺序表的长度
void IncreaseSize(SeqList& L, int len)
{
	int *p = L.data;
	L.data = (int*)malloc((L.MaxSize + len)*sizeof(int));
	for (int i = 0; i < L.length; i++){
		L.data[i] = p[i];       //将数据复制到新区域
	}
	L.MaxSize = L.MaxSize + len;//顺序表的长度增加len
	free(p);                    //释放原来的内存空间
}

// 顺序表的销毁
void SeqListDestory(SeqList& L)
{
	free(L.data);
	L.data = NULL;
	L.length = L.MaxSize = 0;
}

// 打印动态顺序表
void SeqListPrint(SeqList& L)
{
	for (int i = 0; i < L.length; i++){
		printf("%d->", L.data[i]);
	}
	printf("\n");
}

// 顺序表头插
void SeqListPushFront(SeqList& L, ElemType x)
{
	if (L.length >= L.MaxSize)
		IncreaseSize(L, InitSize);  //容量不够则扩容
	for (int i = L.length; i >= 1; i--)
		L.data[i] = L.data[i - 1];  //顺序表元素依次后移
	L.data[0] = x;
	L.length++;
}

// 顺序表头删
bool SeqListPopFront(SeqList* L, ElemType x)
{
	if (L == NULL || L->length <= 0)
		return false;
	for (int i = 1; i < L->length; i++)
		L->data[i - 1] = L->data[i];
	L->length--;
}

// 顺序表尾插
void SeqListPushBack(SeqList& L, ElemType x)
{
	if (L.length >= L.MaxSize)
		IncreaseSize(L, InitSize);   //容量不够则扩容
	L.data[L.length] = x;
	L.length++;
}

// 顺序表尾删
bool SeqListPopBack(SeqList* L)
{
	if (L == NULL || L->length <= 0)
		return false;
	L->length--;
	return true;
}

// 顺序表的按位查找
// 时间复杂度O(1)
ElemType GetElem(SeqList L, int i)
{
	return L.data[i - 1];
}

// 顺序表的按值查找
// 平均时间复杂度O(N)
int LocateElem(SeqList L, ElemType e)
{
	for (int i = 0; i < L.length; i++){
		if (L.data[i] == e)
			return i + 1;  //数组下标为i的元素等于e，返回其位序i+1
		return 0;          //退出循环，说明查找失败
	}
}

// 插入操作（按位序插入）
bool SeqListInsert(SeqList& L, int i, ElemType x)
{
	if (i < 1)        //判断i的范围是否有效
		return false;
	if (i >= L.MaxSize) //当前存储已满，进行扩容
		IncreaseSize(L, InitSize);

	for (int j = L.length; j >= i; j--)
		L.data[j] = L.data[j - 1];
	L.data[i - 1] = x;
	L.length++;
	return true;
}

// 按位序删除
bool SeqListErase(SeqList& L, int i)
{
	if (i<1 || i>L.length)   //判断删除的范围是否有效
		return false;

	for (int j = i; j < L.length; j++)
		L.data[j - 1] = L.data[j];
	L.length--;
}

// 按指定元素删除
void SeqListRemove(SeqList& L, ElemType x)
{
	int pos = LocateElem(L, x);

	while (pos < L.length){
		L.data[pos - 1] = L.data[pos];
		pos++;
	}
	L.length--;
}

// 修改某个位置的值
void SeqListModify(SeqList& L, int pos, ElemType x)
{
	L.data[pos - 1] = x;
}

// 冒泡排序
void SeqListBubbleSort(SeqList L)
{
	int i = 0, j = 0;
	for (i; i < L.length - 1; i++)
	{
		for (j; j < L.length - i - 1; j++)
		{
			if (L.data[j] >L.data[j + 1])
			{
				ElemType tmp = L.data[j];
				L.data[j] = L.data[j + 1];
				L.data[j + 1] = tmp;
			}
		}
	}
}

// 二分查找
int SeqListBinaryFind(SeqList& L, ElemType x)
{
	int left = 0;
	int right = L.length;
	while (left < right)
	{
		int mid = (left + right) / 2;
		if (L.data[mid] == x)
			return mid + 1;
		else if (L.data[mid] < x)
			left = mid + 1;
		else
			right = mid;
	}
	return -1;
}