前缀和的学习

前缀和的学习

当我们想快速的求出来某一个静态数组（中间不会修改的）的某一个区间内所有数的和可以用前缀和来处理。

一维前缀和

假设一个数组a的区间为[L, R]，全部遍历一遍的话时间复杂度是O(N)

for (int i = L; i <= R; i++) {
	res += a[i];
}

当我们需要求很多次的话就可能会超时，那么前缀和就可以快速的让我们算出来某一个区间内所有数的和。

• 思想：
  我们重新预处理一个新的数组s：s[i]= a[1] + a[2] + … + a[i]，s[i]是原数组前i个数的和，特殊规定s[0] = 0；处理s是很快的，因为我们可以发现：
  $$s[i]=s[i-1]+a[i]（公式一）$$
  通过遍历一遍a数组，就可以得到前缀和数组s:

  for (int i = 1; i < n; i++) {
  s[i] = s[i - 1] + a[i];
  }
  

当我们有了s之后，我们想算L到R的和，就可以用s来算了：
$$a[L]+a[L+1]+a[L+2]+...+a[R]=s[R]-s[L-1]（公式二）$$

可以发现，当我们预处理完一个前缀和数组s之后，我们再去算某一段的和就非常容易了。直接算两个数的差就可以了,也就是我们在每一次算和只用一次运算就可以了,每一次查询都优化了时间复杂度：O(N)→O(1)

二维数组前缀和

我们二维前缀和有没有像一维前缀和那样的公式呢？

在一维前缀和中，我们前缀和数组s每一个s[i]表示的是原数组前i个数的和；

在二维中，我们前缀和矩阵的这个数就代表着它在原矩阵中左上角所有元素的和：

所有数全部替换为前缀和矩阵：

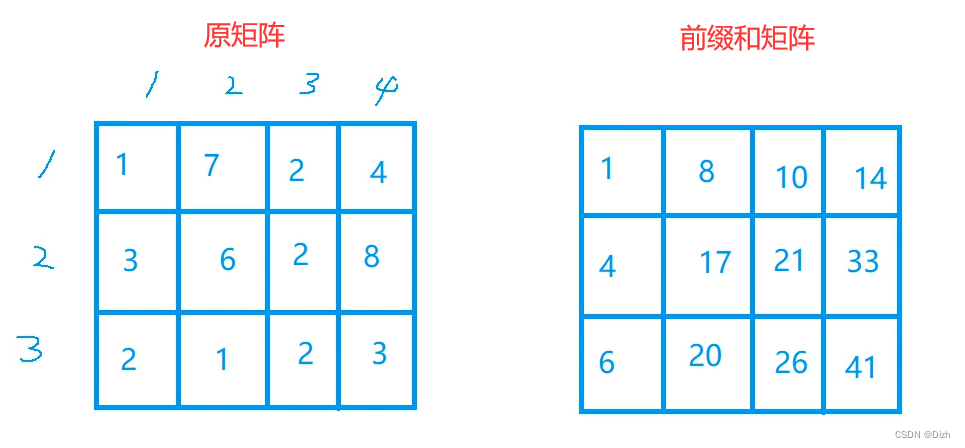
问题一：我们怎么通过原矩阵算出前缀和矩阵？容斥原理

那什么是容斥原理呢？看图：

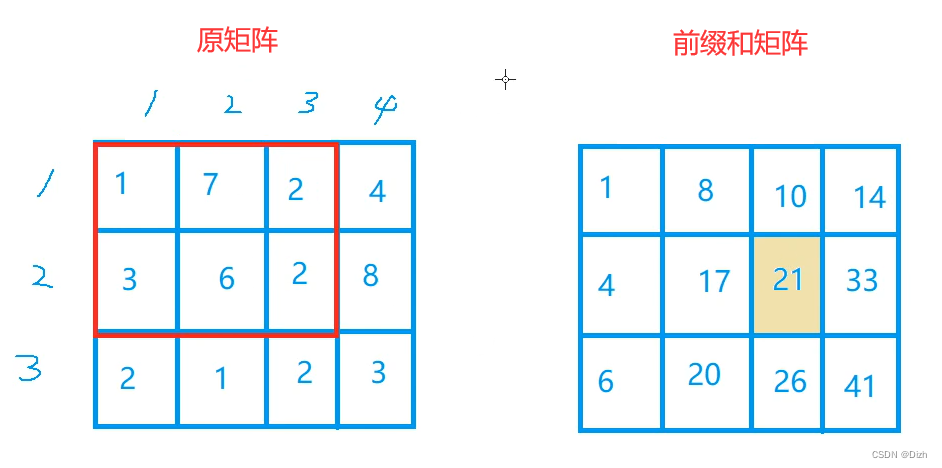
我们可以先求左边的这四个数：

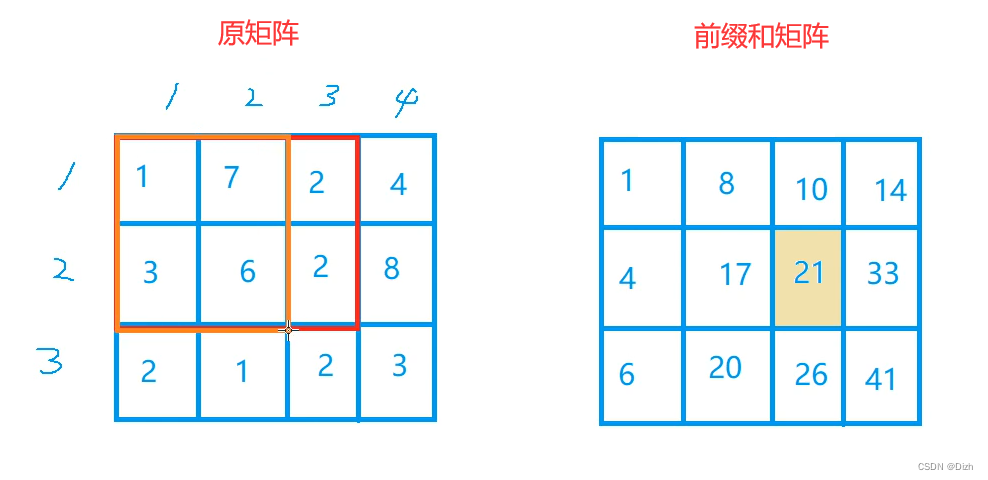
然后再求上面的三个数：

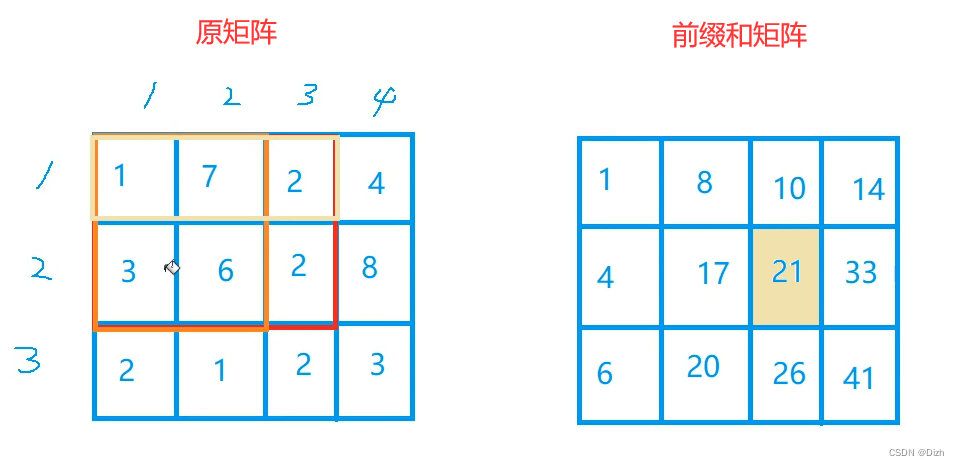
可以发现，黄色的格子被算了一次，蓝色的格子被算了两次，所以我们只需要减去所有蓝色的格子，就可以保证我们除了最后一个本身数的格子以外，所有数都只被加了一次，这样我们再加上此数字就可以得到前缀和矩阵的值。如下图：

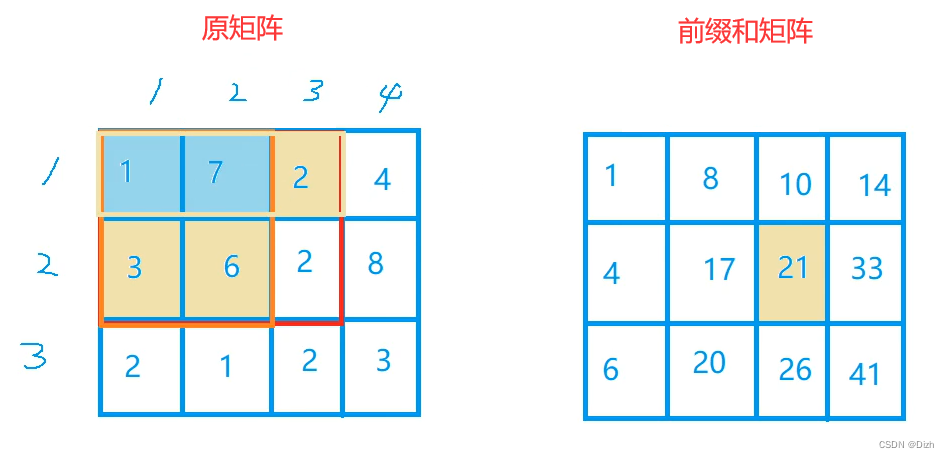
总结：前缀和矩阵的值 = 此格子上面所有数的总和 + 此格子左面所有数的总和 - 重复的格子 + 原数

即为：
$$s[x][y]=s[x-1][y]+s[x][y-1]-s[x-1][y-1]+a[x][y]（公式一）$$

问题二：如何利用前缀和矩阵，计算某一个子矩阵的和？容斥原理

比如我们想计算红方方框子矩阵的和：

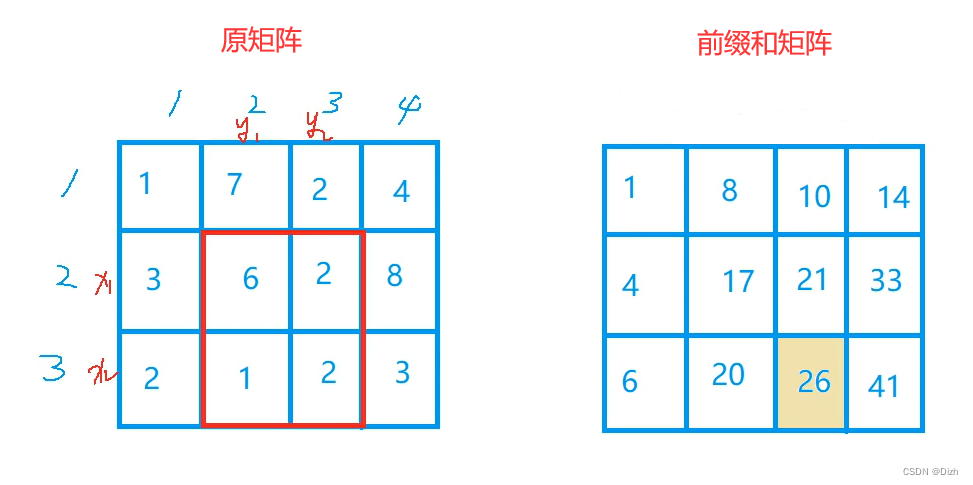
但是我们只能知道黄色方框子矩阵的和：

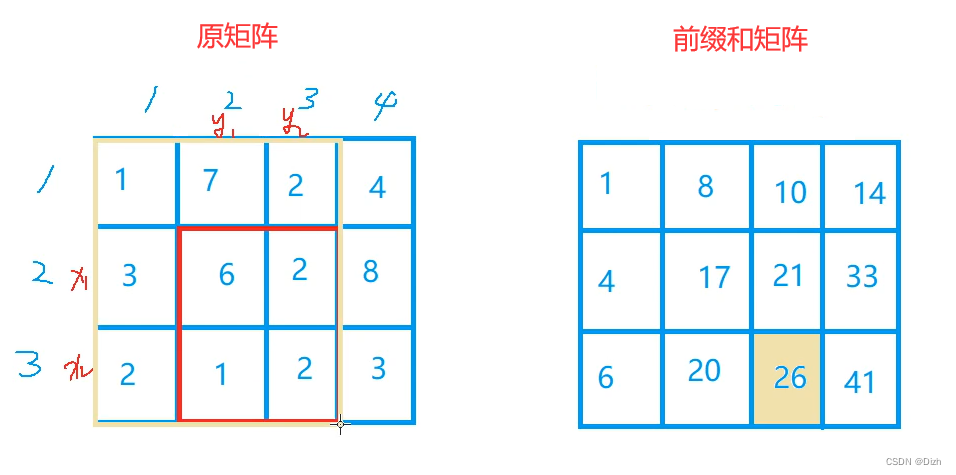
我们需要去掉“倒L”形状的值，这个就可以用容斥原理来去掉，首先去掉左面所有的值，然后再去掉上面的值；
现在黄色格子我们已经全部去掉了，但是灰色格子我们去掉了两次，所以我们还要再加上它一次。

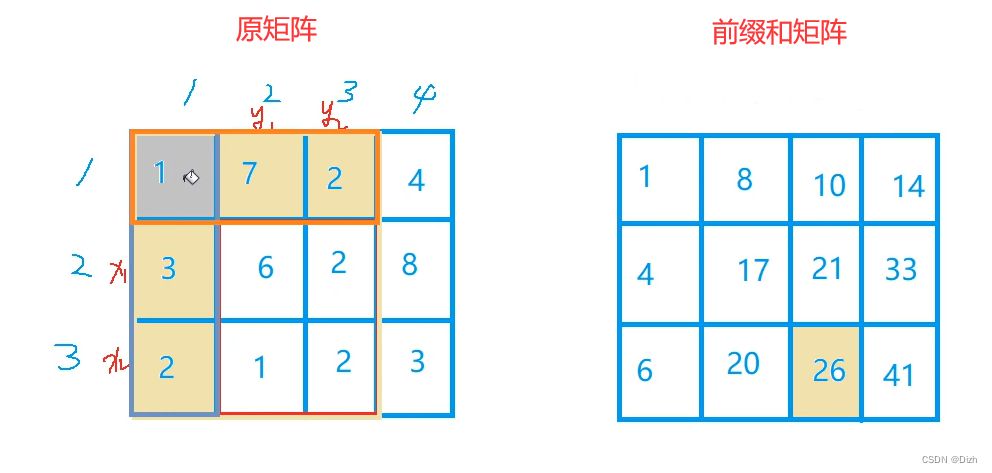
最终公式：以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
$$s[x2,y2]-s[x2,y1-1]-s[x1-1,y2]+s[x1-1,y1-1]（公式二）$$

我们利用前缀合矩阵以常数次计算快速的求出我们某一个子矩阵的和，时间复杂度优化为：O(mn)→O(1)

注：

1. 二维前缀和主要是对一维前缀和的扩展。
2. 容斥原理就是用空间换时间的概念。

参考文章：https://blog.youkuaiyun.com/weixin_53407527/article/details/122908061