HDU多校第八场

1003

题意：给三个点判断顺时针还是逆时针输入

思路：用向量叉积计算即可

代码：

#include<cstdio>
using namespace std;
#define mod 1000000007
#define INF 0x3f3f3f3f
#define pi 3.141592654
typedef long long ll;
const int N = 2e6+5;
struct node{
    ll x,y;
}p[4];
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        for(int i=1;i<=3;i++)
            scanf("%lld %lld",&p[i].x,&p[i].y);
        int pp = 1;
        if ((p[2].x - p[1].x) *(p[3].y - p[1].y) -(p[3].x - p[1].x) *(p[2].y-p[1].y) < 0)
            pp = 0;
        if(pp)  printf("Counterclockwise\n");
        else    printf("Clockwise\n");
    }
    return 0;
}

1006

题意：求一个序列，序列中的第i个数在，第i个区间内，切第i个数郁第i-1个数相差不超过k，如果不存在序列则输出NO

思路：正向扫一遍n个区间，求出所有的可能数，如果到最后一个区间仍是符合要求的话，逆向扫一遍n个区间并存储序列，输出YES和序列，否则输出NO

代码：

1008

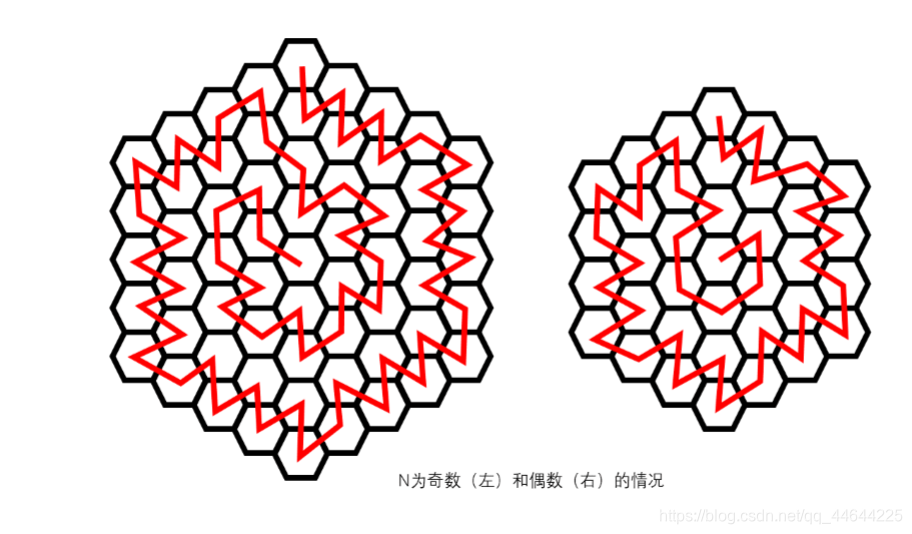
题意：在指定的图形内，要求尽可能多的转向（即前后两次的方向不同），问走完该图形的序列（起点任选）

构造：

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
const int INF = 0x3f3f3f3f;
int a[7] = {0,5,6,1,2,3,4};
int main(){
    int t,n;scanf("%d",&t);
    while (t --){
        scanf("%d", &n);
        while(n > 2){
            printf("6");
            for(int i = 1 ;  i<= 6 ; i++){
                printf("%d",i);
                for(int j=1 ; j<= n - 2 - (i==6); j ++)
                    printf("%d%d",a[i],i);
            }
            printf("1");
            n-=2;
        }
        if (n == 2)   printf("612346");
        puts("");
    }
    return 0;
}

1009

题意：一个长度为n字符串，对于n的因子k，把这个字符串n分成n/k（要求大于1），如果存在这样一个K使得所有的n/k个子串都构成同一个圆排列，即输出YES，否则输出NO

思路：对于s的因子（最多20个因子）k，我分解出k个子串，每个子串的长度是n/k; 对于第一个子串，我可以求出出他所有同构的串（一共n/k个）的hash值对于后面的k-1个串就之间对照hash值就行了，只要出现新的hash值就不能分解成k个子串

队友代码：与我的想法略不同，求出所有子串对应的最小hash值，如果可以达成目标，则所有子串对应的hash值都应该相同。

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
#define p 13331
char ch[5000100];
ull ha[5000100];
ull mi(ull a,ull b){
    if(a<b)        return a;
    return b;
}
ull qpow(ull x,ull n){
    ull z=x;
    ull ans=1;
    while(n){
        if(n&1)
            ans=ans*z;
        n>>=1;
        z*=z;
    }
    return ans;
}
int main(){
    int z;
    scanf("%d",&z);
    while(z--){
        int n;
        scanf("%d",&n);
        scanf("%s",ch+1);
        int anss=0;
        for(int k=1;k<=n/2;k++){
            if(n%k==0){
                int shu=n/k;
                ha[0]=0;
                for(int i=1;i<=shu;i++){
                    ha[i]=0;
                    int t=(i-1)*k+1;
                    for(int j=t;j<t+k;j++)
                        ha[i]=ha[i]*p+(ull)ch[j];
                    ull s=ha[i];
                    ull zong=qpow(p,k-1);
                    for(int j=t+1;j<t+k;j++){
                        s=s-zong*(ull)ch[j-1];
                        s=s*p+(ull)ch[j-1];
                        ha[i]=mi(ha[i],s);
                    }
                }
                ull r=ha[1];
                int f=0;
                for(int i=2;i<=shu;i++){
                    if(ha[i]!=r){
                        f=1;break;
                    }
                }
                if(f==0){
                    anss=1;break;
                }
            }
        }
        if(anss==1)     printf("Yes\n");
        else     printf("No\n");
    }
}