7-33 Pop Sequence (25分)（完整模拟思路+极短代码）

最新推荐文章于 2024-07-09 01:55:28 发布

原创最新推荐文章于 2024-07-09 01:55:28 发布 · 501 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #栈

PTA 团队天梯赛专栏收录该内容

36 篇文章

订阅专栏

本文介绍了一种判断合法出栈序列的算法，通过模拟入栈和出栈过程，结合一维数组存储出栈序列，实现对序列合法性的判断。算法详细解释了入栈、判断栈大小和出栈的步骤，并提供了C++代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

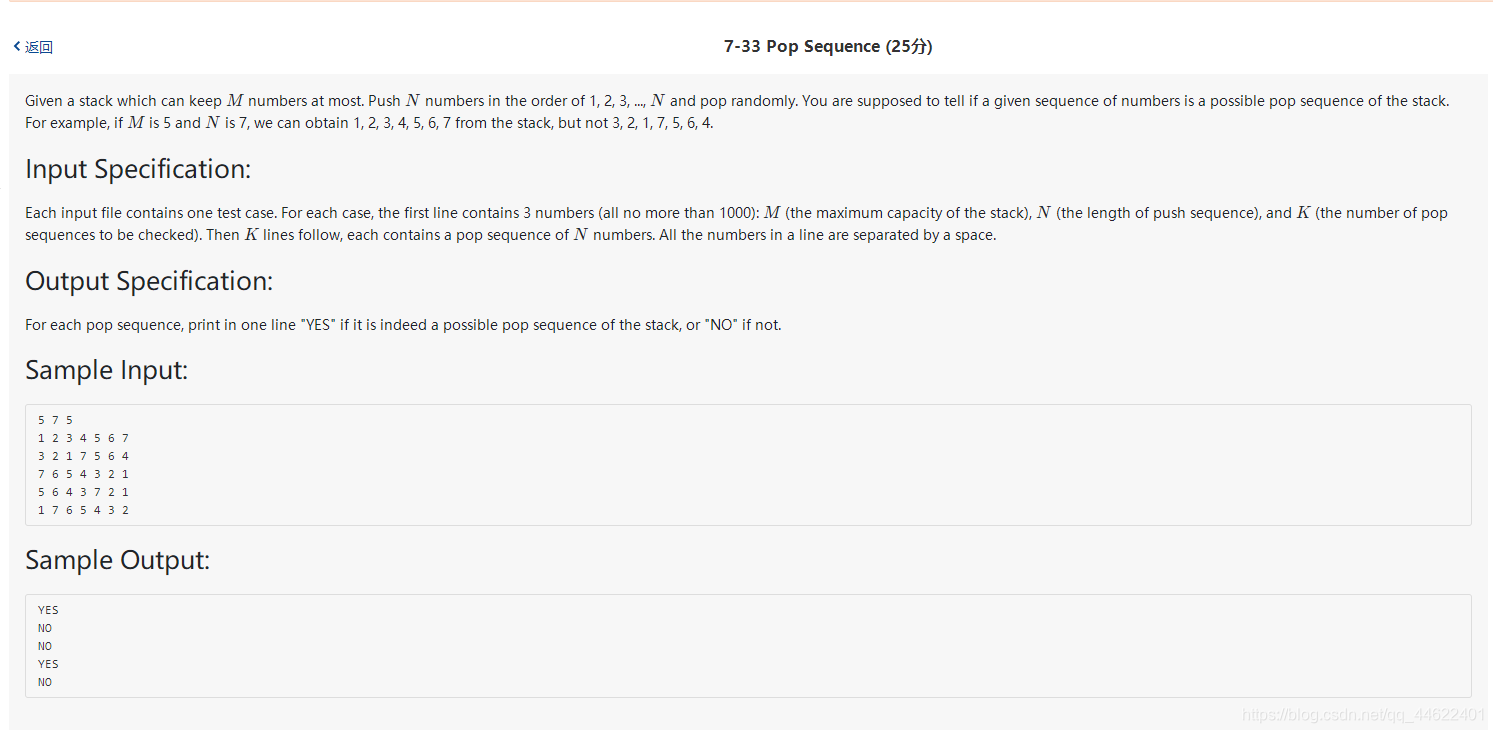
在这里插入图片描述
这道题就是判断合法出栈序列。大致思路如下：
因为已知入栈顺序为1，2，3，4，，，n。所以首先建立一个栈用来模拟进栈，然后建立一个一维数组用来存储每次输入的出栈序列。然后进栈的时候如果栈顶与当前一维数组的数相等，就把栈顶删除，一维数组当前的下标+1，以此类推，如果不相等，就再入栈（此时如果入栈后栈的大小大于最大容量，则不合法）。最后根据栈是否为空.来判断是否合法。下面举个简单的例子可以帮助你理解这个思路。

比如说入栈序列为1->n 出栈序列为3 2 1 7 5 6 4.
第一步：1入栈，判断栈的大小是否合法（合法），判断栈顶是否与当前数组下标的数相同（1！=3）

第二步：2入栈，判断栈的大小是否合法（合法），判断栈顶是否与当前数组下标的数相同（2！=3）

第三步：3入栈，判断栈的大小是否合法（合法），判断栈顶是否与当前数组下标的数相同（3= =3）
此时删除栈顶（栈内只剩1 2），数组下标加1（此时指向2）。然后再次判断栈顶是否与当前数组下标
的数相同（2= =2）.，所以删除栈顶（栈内只剩1），数组下标加1（此时指向1）.然后再次判断栈顶是
否与当前数组下标的数相同（1= =1），所以删除栈顶（栈为空），数组下标加1（此时指向7）.然后再
次判断栈顶是否与当前数组下标的数相同（栈为空所以不相同）。

第四步：4入栈，判断栈的大小是否合法（合法），判断栈顶是否与当前数组下标的数相同（4！=7）

第五步：5入栈，判断栈的大小是否合法（合法），判断栈顶是否与当前数组下标的数相同（5！=7）

第六步：6入栈，判断栈的大小是否合法（合法），判断栈顶是否与当前数组下标的数相同（6！=7）

第七步：7入栈，判断栈的大小是否合法（合法），判断栈顶是否与当前数组下标的数相同（7= =7）
所以删除栈顶（栈内只剩4 5 6），数组下标加1（此时指向5），然后再次判断栈顶是否与当前数组下标的
数相同（6！=5）

第八步：此时入栈序列已经完毕，但是栈不为空（4 5 6还在栈内），所以可以证明3 2 1 7 5 6 4这个出栈序列不合法。

根据上面的步骤，你可以发现其实这个判断过程大致分为三步，入栈，判断栈大小，出栈。于是我门就可以根据这个步骤来写代码。（其实解题的过程就是这样，先自己模拟，然后找规律找可以合并的地方，划分成几个步骤，最后用代码表示出来，再根据初次运行结果慢慢调试更改）。代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[10010],m,n,k,flag;
int main()
{
	cin>>n>>m>>k;
	while(k--)
	{
		stack<int>s;
		for(int i=1;i<=m;i++)	cin>>a[i];
		int pos=1,num=1,flag=0;
		while(pos<=m)
		{
			s.push(num++);
			if(s.size()>n)	{flag=1;break;}
			while(!s.empty()&&a[pos]==s.top()&&pos<=m)
			{
				s.pop();
				pos++;
			}
		}
		if(flag)	cout<<"NO"<<endl;
		else if(!flag&&s.empty())	cout<<"YES"<<endl;
	}
}