C0250 [2004普及组-C]FBI树（数据结构基础二叉树（创建+三种遍历方式））

最新推荐文章于 2023-05-29 18:27:45 发布

原创最新推荐文章于 2023-05-29 18:27:45 发布 · 339 阅读

0 ·

CC 4.0 BY-SA版权

完全二叉树（建立+三种遍历）专栏收录该内容

3 篇文章

订阅专栏

本文详细介绍了如何使用链式结构构建二叉树，并通过递归实现了前序、中序和后序遍历。文章重点讲解了二叉树结构体定义、指针基本知识及内存分配，并提供了AC代码实例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

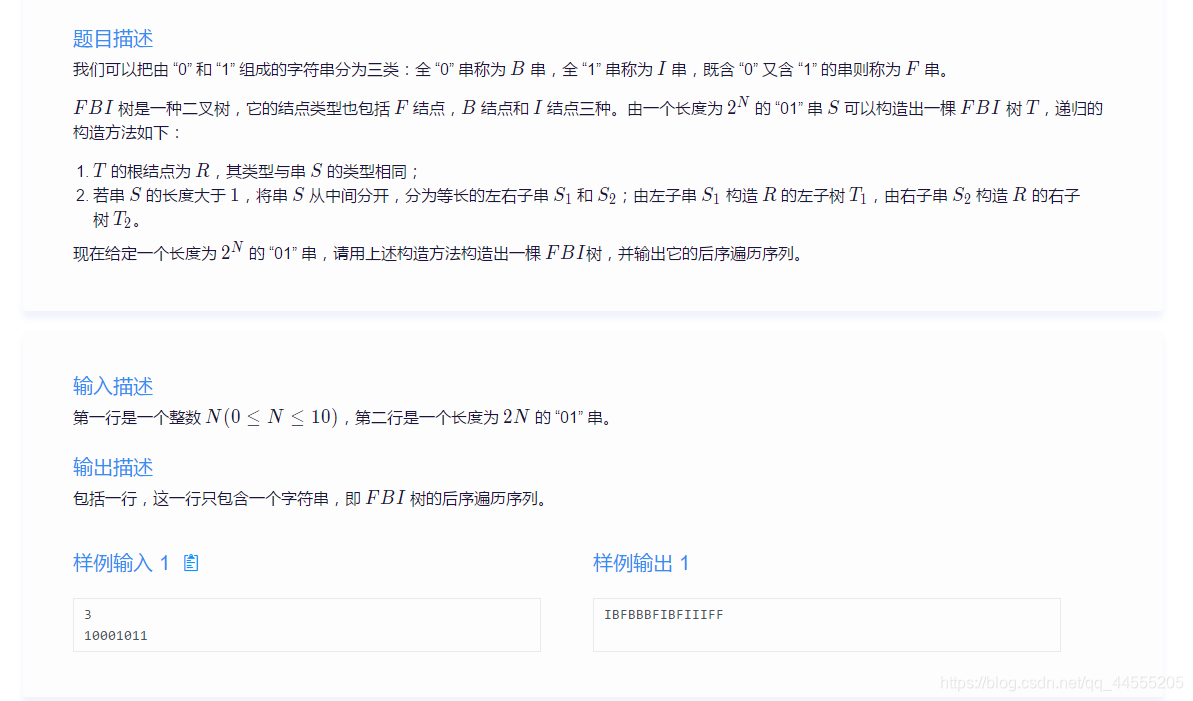
在这里插入图片描述这道题我终于把二叉树搞懂了，从遍历到创建好不容易哦（以前没看懂二叉树，QAQ）；
我觉得这道题就是一个很好的关于二叉树的一个简单应用；
首先，我不管二叉树树应该怎么建立，首先来看完全二叉树的图的表示结构：
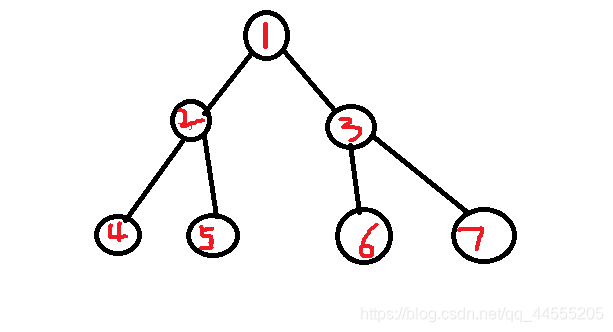
在这里插入图片描述
这里编号不能变，因为这里可以用顺序存储来构建完全二叉树（segment tree就是用的数组构建的）;
但是我这里的问题要利用链式结构来建立二叉树；
首先应该知道树的基本术语（书上有这里不解释了）和二叉树的结构体的定义；
二叉树的结构体定义：

struct Node{
	char data;//这里只是我写成了char 类型，其实也可以是其他的（主要是为了解决这道题）
	Node *left_child,*right_child;
};

那么知道这个之后；我还应该知道指针的基本知识（关于分配内存的问题）：
如果形式为这样的声明：

类型名 *p;

就表明还没有给p所应该指向的内存分配合理的内存（也就是p还没有指向具体的地址）；
那么指针的分配内存的方式我知道的就只有三种：

1.类型名 *p=new 类型名;//注意这里类型名都必须是同类型的
2.类型名 *p=other_p;//指向 同类型的0other_p所指向的内存首地址
3.类型名 *p=&other_varible;//指向一个同类型的变量地址

从内存上面去理解：
对于第1点（new运算符其实就是自己建一个内存返回这个内存的首地址）：

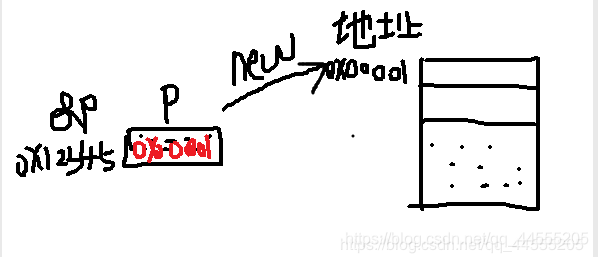
在这里插入图片描述
这里就是p本身的内存是用来存其他变量的地址，而利用取地址操作符就可以取出p本身的地址（这里的地址知识我随意举的哈）
然后利用指针访问的语法规则就可以知道了；其实第2,3点的本质上的理解都是一样的；
所以回到这道题上面来，我应该如何利用链式结构（在逻辑上相邻，但是物理存储上可能不相邻）来建立二叉树呢？
这里先理解三种遍历方式：
1.前序遍历（因为这里是最不好理解的，所以我把每次递归都做上标记，这样就可以更好的区分每次递归到的状态）：

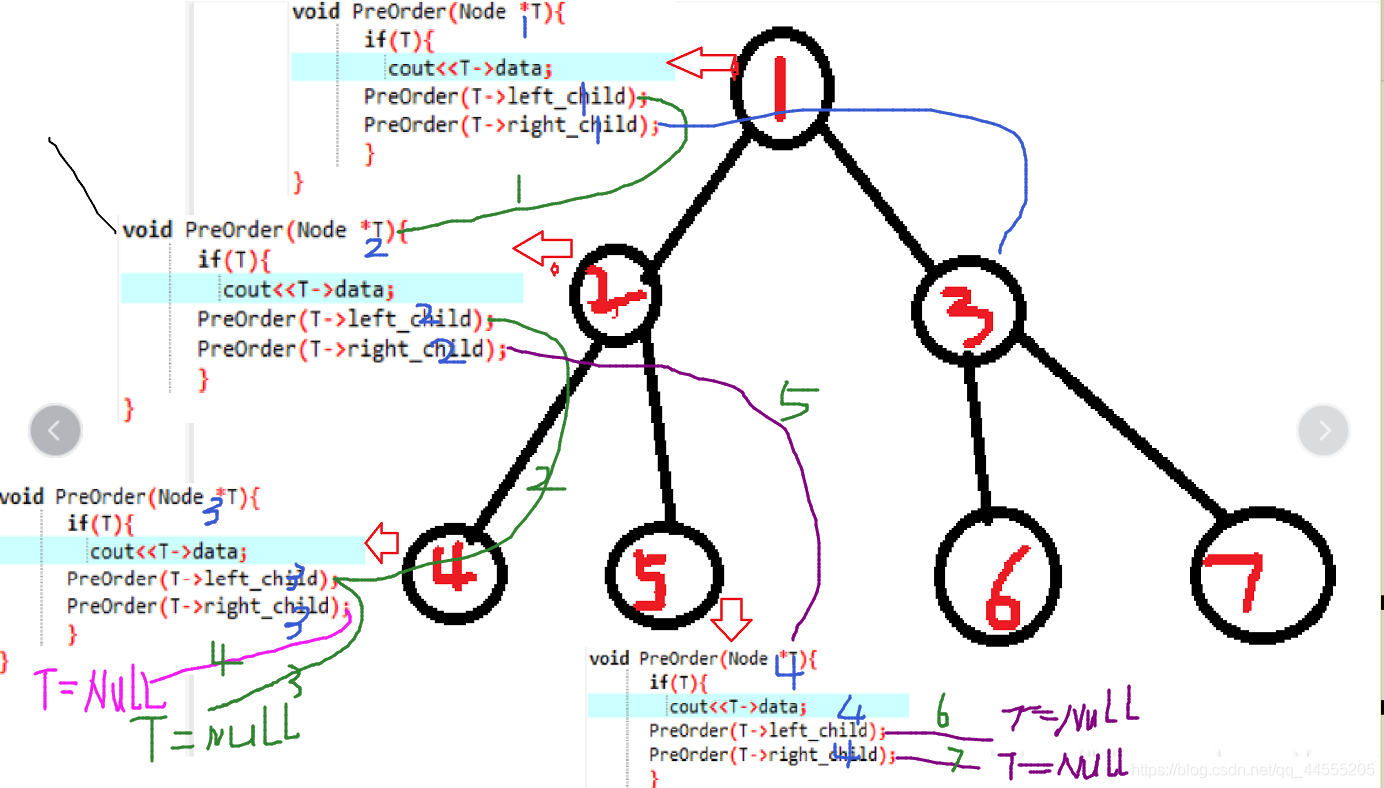
在这里插入图片描述
这里需要很清楚的知道，程序在一个函数里面是整体的严格的从上往下执行；那么上图我为了更好理解就把递归的状态用蓝色的数字写了出来，然后每次到最低端的是后，根据程序的执行规则，我就可以很清楚的来想出下一步它应该走哪里（这里用的绿色的数字标记的）；只要理解了这个问题，那么后面的两种中序，后续就按照同样的方式理解就可以理解了（这里要求对指针有很熟悉的理解才会看明白）；
所以这道题就是很基础的二叉树题目；但是需要注意：
每次我到了一个节点（也就是一个状态，我就应该判断他下面的还用不用new内存（看下面是否还应该有状态））（因为我把本状态（本节点）操作完了之后，我就会判断下面还需不需要节点，如果不需要，我就把本节点的left_child和right_child==NULL）；注意：在建立二叉树的时候需要一个全局Node类型的指针，并且需要new，不然根节点哪里来呢（✧*｡٩(^㉨)و✧｡）？
AC代码：

#include<bits/stdc++.h>
using namespace std;
struct Node{
	char s;
	Node *left_child,*right_child;
};
Node *head;
int n;
char s4[6000];
void init(){
	  scanf("%d%s",&n,s4);
	  head=new Node;//根节点应该new一个内存！！！！ 
}
void BuildTree(Node *T,int l,int r){
  int flag1=0,flag2=0;
  for(int i=l;i<=r;i++){
  	  if(s4[i]=='0') flag1=1;//B
  	  else flag2=1;//I
  }
  if((flag1)&&(!flag2)) T->s='B';
  if((!flag1)&&(flag2)) T->s='I';
  if(flag1&&flag2) T->s='F';//因为这里需要把本节点（本状态）操作完成之后才对它的两个孩子操作 
	  if(l<r){
	  	  T->left_child=new Node;T->right_child=new Node;
	  	  int mid=(r+l)/2;
	  	  BuildTree(T->left_child,l,mid);
	  	  BuildTree(T->right_child,mid+1,r);
	  }else{
	  	  T->left_child=NULL;//把他的两个孩子指向NULL 
	  	  T->right_child=NULL;
	  	  return;
	  }
	  
   
}
////前序遍历
//void PreOrder(Node *T){
//	   if(T){
//	   	  printf("%c",T->s);
//	   	  PreOrder(T->left_child);
//	   	  PreOrder(T->right_child);
//	   }
//} 
////中序遍历
//void InOrder(Node *T){
//	  if(T){
//	  	  InOrder(T->left_child);
//	  	  printf("%c",T->s);
//	  	  InOrder(T->right_child);
//	  }
//} 
//后续遍历 
void PostOrder(Node *T){
	  if(T){
	    PostOrder(T->left_child);
	    PostOrder(T->right_child);
       printf("%c",T->s);
	    return;
      }
}
int main(){
  init();//注意初始化，这样写的好处是函数分工明确 
  BuildTree(head,0,strlen(s4)-1);//建立二叉树 
  PostOrder(head);//后序遍历
//  cout<<endl;
//  PreOrder(head);//前序遍历
//  cout<<endl;
//  InOrder(head);//中序遍历
//  cout<<endl;
	return 0;
}

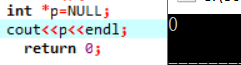
常识小提醒(NULL地址为0)：
在这里插入图片描述