B. Mike and Children--暴力+题目拓展--Codeforces Round #543 (Div. 2, based on Technocup 2019 Final Round)

Mike and Children

time limit per test 2 seconds
memory limit per test 256 megabytes

题目链接http://codeforces.com/contest/1121/problem/B

---

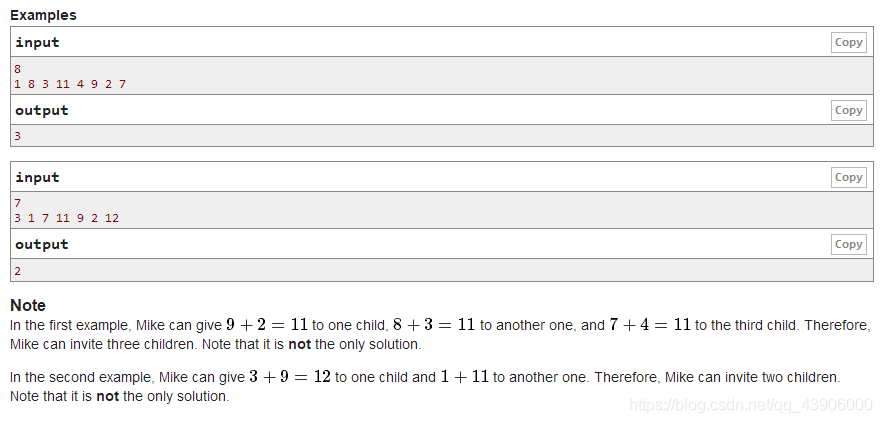
题目大意：给你n个数，让你求最多的对数使得每对的数字之和相同，比如样例1：
9+2=11 、 8+3=11 、 7+4=11最多3对。

看看题目2s，再看看数据一个1e3,一个1e5，加上和的条件就是2e5。。。然后我们就可以想象得到了:1e3* 2e5直接暴力过去就是差不多2s了。。。因为它规定了每个数只出现了一次，那么我们直接看看vis[枚举的数-a[i]]是否=1就行了。如果可以的话计数器cnt++，最后的答案就是cnt/2，因为我们把整个a数组都跑了一遍，有一半的会重复。

当然，本蒟蒻刚开始的时候没注意a_i!=a_j也就是说会有数重复，那么应该怎么搞呢?当然也是暴力。。。不过T了，这里用到了map的优化unordered_map

以下是带重复数字的一份代码QAQ没有经过测试，前9组数据可以跑过去，如果遇到非T的情况请指出批评QAQ：

#include <bits/stdc++.h>
using namespace std;
const int mac=1e5+10;
int n,vis[mac],a[1010];
int v[1010*1010],ans[1010][1010];
int ok(int x)
{
	unordered_map<int,int>q;
	int sum=0;
	for (int i=1; i<=n; i++){
		if (a[i]>=x) continue;
		if (a[i]==x-a[i] && q[a[i]]+2>vis[a[i]]) continue; 
		if (q[a[i]]+1>vis[a[i]] || q[x-a[i]]+1>vis[x-a[i]]) continue;
		sum++;
		q[a[i]]++;q[x-a[i]]++;
	}
	return sum;
}
int main()
{
	scanf ("%d",&n);
	int mi=9999999,mx=-10;
	for (int i=1; i<=n; i++){
		scanf ("%d",&a[i]);
		mi=min(mi,a[i]);
		mx=max(mx,a[i]);
		vis[a[i]]++;
	}
	for (int i=1; i<=n; i++)
	 for (int j=i+1; j<=n; j++)
	  ans[i][j]=a[i]+a[j],v[ans[i][j]]++;
	int ans=1;
	for (int i=mi+1; i<=mx*2; i++){
		if (v[i]<=1) continue;
		int p=ok(i);
		ans=max(ans,p);
	}
	cout<<ans<<endl;
	return 0;
}

以下是本题的AC代码：

#include <bits/stdc++.h>
using namespace std;
const int mac=1e5+10;
int n,vis[mac],a[1010];
int main()
{
	scanf ("%d",&n);
	int mi=9999999,mx=-10;
	for (int i=1; i<=n; i++){
		scanf ("%d",&a[i]);
		mi=min(mi,a[i]);
		mx=max(mx,a[i]);
		vis[a[i]]=1;
	}
	int ans=1;
	for (int i=mi+1; i<=mx*2; i++){
		int cnt=0;
		for (int j=1; j<=n; j++){
			if (a[j]>=i) continue;
			if (vis[i-a[j]]==1) cnt++;
		}
		ans=max(ans,cnt/2);
	}
	cout<<ans<<endl;
	return 0;
}