C. Alarm Clocks Everywhere---欧几里得算法的运用--- Educational Codeforces Round 63-优快云博客

博客围绕题目“Alarm Clocks Everywhere”展开，该题给出n个起始时间和m个闹钟，需判断能否提醒n个时间并输出一组y和闹钟位置。解题时y取a[1]，闹钟提醒时间为a[2]-a[1]等，要找能被这些数整除的数，用到欧几里得算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Alarm Clocks Everywhere

time limit per test 3 seconds
memory limit per test 256 megabytes

题目链接http://codeforces.com/contest/1155/problem/C

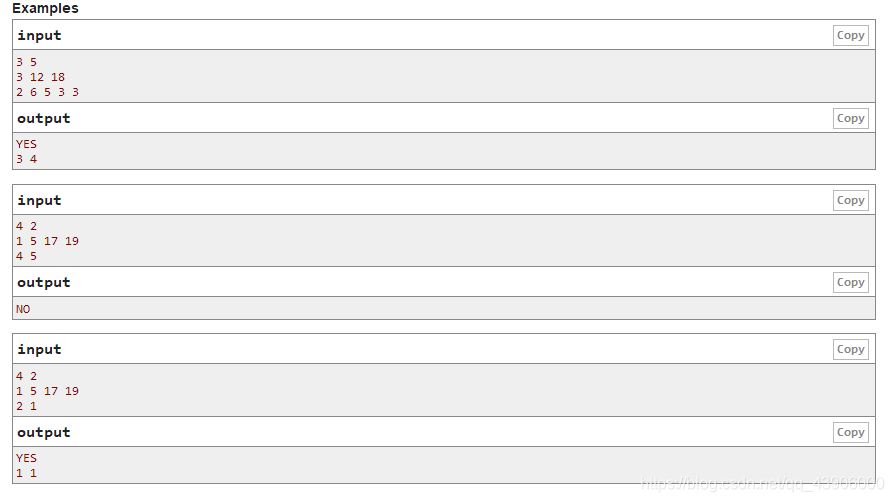
在这里插入图片描述

emmm,读题是硬伤。。。读了将近20分钟题。。。
题目大意：给你n个起始时间和m个闹钟，对于每个闹钟，你可以定义它的开始响的时间y，然后它会每隔p_i分钟响一下，问你是否能提醒这n个时间，如果能请随意输出一组y和选择的闹钟的位置。。。

其实y很好求，就是a[1]，由于我们要把n个时间都提醒，所以最小的a[1]就一定会是一个闹钟响的时间，我们可以将它定义为y。

接下来闹钟的提醒时间应该是a[2]-a[1]、……a[n]-a[1]。那么我们就要找一个数可以被他们所有整除。于是，欧几里得（gcd）就出来了。

以下是AC代码：

#include <bits/stdc++.h>
using namespace std;
const int mac=3e5+10;
#define ll long long
ll a[mac],b[mac];
ll gcd(ll a,ll b)
{
	return b==0?a:gcd(b,a%b);
}
int main()
{
	int n,m;
	scanf ("%d%d",&n,&m);
	for (int i=1; i<=n; i++)
	 scanf ("%lld",&a[i]);
	for (int j=1; j<=m; j++)
	 scanf ("%lld",&b[j]);
	for (int i=2; i<=n; i++)
	 a[i]-=a[1];
	ll gm=gcd(a[2],a[3]);
	for (int i=4; i<=n; i++)
	  gm=gcd(gm,a[i]);
	for (int i=1; i<=m; i++)
	  if (gm%b[i]==0) {
	  	printf ("YES\n");
	  	printf ("%lld %d\n",a[1],i);
	  	return 0;
	  }
	printf ("NO\n");
	return 0;
}