回归vs分类
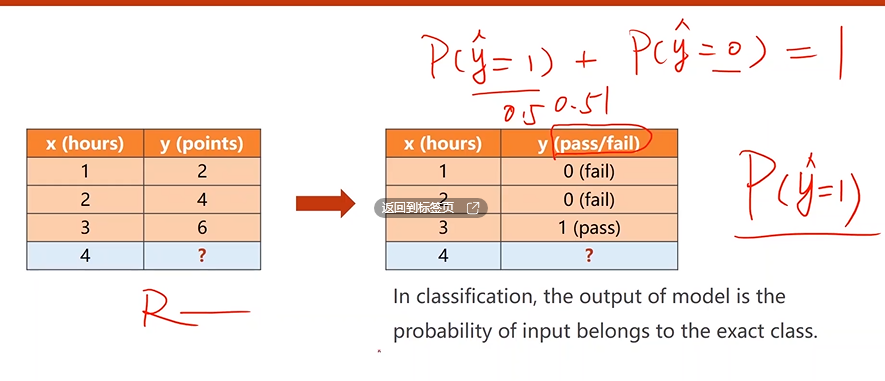
- 回归是预测数值
- 分类是预测类别概率
sigmoid函数
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/be5461efa5e337e422bd8c52e73c2c49.png)
Logistic Function是最典型的sigmoid函数,因此有些书会直接说成sigmoid函数。
实际上满足如下条件即可称为sigmoid函数:
- 饱和函数
- 单调递增
- 存在极限
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/f76e62eb2939c983c47e939c528e93f6.png)
损失函数
使用二分类交叉熵公式:
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/e9313c8bdfa6b14eb145f2c4623e8661.png)
- y=1,预测值接近1,loss减小
- y=0,预测值接近0,loss减小
例子
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/9f6b1c5f9cb9367e09ecd2b44460bdb9.png)
- 多个loss,MiniBatch求均值
课堂练习
模型实现
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/ea15020f8940e8d2ec8c00be94e10848.png)
可以看到init部分没有区别,因为逻辑回归没有参数增加。
计算损失
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/aa6bdc8feeb31991c9541bb244c6112f.png)
实现代码
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/0e43e4fca68551d0e0ae6519d25aa381.png)
import torch
import matplotlib.pyplot as plt
#1.准备数据集
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[2.0],[4.0],[6.0]])
#2.使用Class设计模型
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LinearModel,self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self,x):
y_pred = F.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel() #创建类LinearModel的实例
#3.构建损失函数和优化器的选择
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)
#4.进行训练迭代
epoch_list =[]
loss_list=[]
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred,y_data)
print(epoch,loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_list.append(epoch+1)
loss_list.append(loss.item())
# 画图
plt.plot(epoch_list,loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/6b92b8870586757388e62ba926d8d7aa.png)
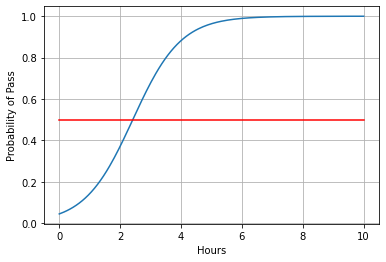
测试模型
![[图片]](https://i-blog.csdnimg.cn/blog_migrate/f71d6221f76a2fa9ef5e3845f1796d3b.png)
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(0,10,200)
x_t=torch.Tensor(x).view((200,1))
# 使用训练好的模型
y_t=model(x_t)
y=y_t.data.numpy()
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()
学习资料
系列文章索引
教程指路:【《PyTorch深度学习实践》完结合集】 https://www.bilibili.com/video/BV1Y7411d7Ys?share_source=copy_web&vd_source=3d4224b4fa4af57813fe954f52f8fbe7























 1086
1086

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










