【剑指offer-C++】JZ27：二叉树的镜像

题目描述

描述：操作给定的二叉树，将其变换为源二叉树的镜像。

数据范围：二叉树的节点数 0≤n≤1000 ， 二叉树每个节点的值 0≤val≤1000。

要求： 空间复杂度 O(n) 。本题也有原地操作，即空间复杂度 O(1) 的解法，时间复杂度 O(n)。

比如：源二叉树：

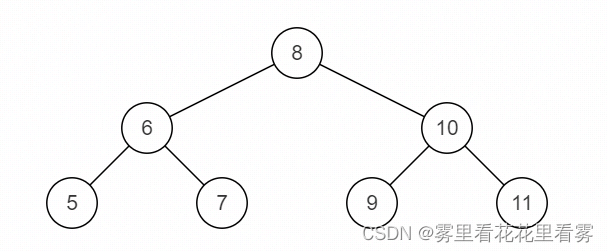
镜像二叉树：

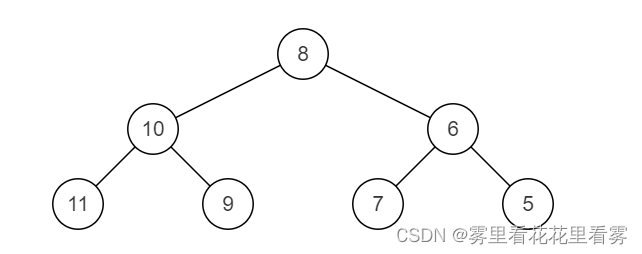
输入：{8,6,10,5,7,9,11}
返回值：{8,10,6,11,9,7,5}
说明：如题面所示  

输入：{}
返回值：{}

解题思路

二叉树的镜像：最直观的想法是，交换每一个结点的左右孩子结点。首先编写一个函数toMirror，用于交换每一个结点的左右孩子结点，其参数为TreeNode类型指针，返回值为void，当当前结点指针为空时返回，否则使用swap交换左右子树，然后先对当前结点的左孩子使用toMirror，再对当前结点的右孩子使用toMirror。在给定函数Mirror中，首先判断根结点是否为空，如果是则返回nullptr，否则调用toMirror，然后再返回根结点。

//交换左右子树
void toMirror(TreeNode * cur)
{
   if(!cur) //当前结点为空则返回
     return;
   swap(cur->left,cur->right); //交换左右子树
   toMirror(cur->left); //左子树镜像
   toMirror(cur->right); //右子树镜像
}
TreeNode* Mirror(TreeNode* pRoot) 
{
   if(!pRoot)
     return nullptr;
   toMirror(pRoot);
   return pRoot;
}

优化：对比上述边界条件以及函数头可知，可以将两者进行结合，从而变成一个函数。曾经我对递归一直有疑问，尤其是二叉树这一部分，到底是一个函数还是两个函数，到底是前序遍历、中序遍历还是后序遍历……但其实对于二叉树以及递归不是很熟悉的话，可以先按照自己的解题思路来，再将解题思路慢慢转化为实现代码，再进行一步步的优化，练习多了自然就会有经验啦。

TreeNode* Mirror(TreeNode* pRoot) 
{
    if(!pRoot) //当前结点为空则返回
      return nullptr;
    swap(pRoot->left,pRoot->right); //交换左右子树
    Mirror(pRoot->left); //左子树镜像
    Mirror(pRoot->right); //右子树镜像
    return pRoot; //返回根结点
}