二进制索引树详解-优快云博客

本文深入讲解了二进制索引树（Binary Indexed Tree）这一高效数据结构的实现原理与应用。从lowbit魔法函数到单点修改、区间查询的实现，再到通过HDU1166模板题的实际应用，全面解析了二进制索引树在区间求和等场景下的优势。

首先呢，这个可爱的数据结构大概是长介个样儿哒

咳咳先放一个讲的贼好的连接look here(下图是转的哇

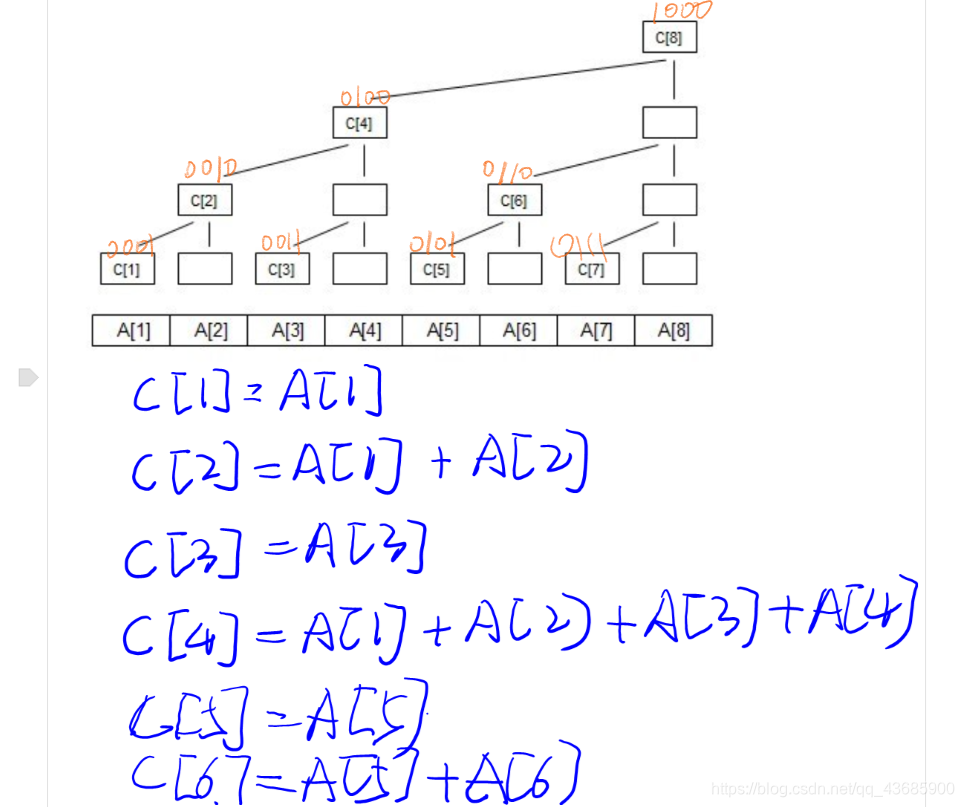
额看这张图（蕴含神奇的二进制

上面那个连接讲的贼好我就不赘述了qaq 来整理下板子

lowbit魔法

int lowbit(int x){
    return x & (-x);
}

单点修改

int add(int pos,int ad){
    for(int i = pos;i <= n; i += lowbit(i)){
        tree[i] += y;
    }
}

区间查询

int getsum(int x){
    int ans = 0;
    for(int i = x;i > 0; i -= lowbit(i)){
        ans += tree[i];
    }
    return ans;
}

然后emmm写道模板题HDU1166嘻嘻嘻

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>

using namespace std;
const int maxn = 5e4 + 5;

int t,n,haha,pos,ad;
int tree[maxn];
string cur;

int lowbit(int t){
	return t & (-t);
}

void add(int x,int y){
	for(int i = x;i <= n; i += lowbit(i)){
		tree[i] += y;
	}
}

int getsum(int x){
	int ans = 0;
	for(int i = x;i > 0;i -= lowbit(i)){
		ans += tree[i];
	}
	return ans;
}

int main()
{
	scanf("%d",&t);
	for(int i = 1;i <= t; i++){
		memset(tree,0,sizeof(tree));
		scanf("%d",&n);
		for(int j = 1;j <= n; j++){
			scanf("%d",&haha);
			add(j,haha);
		}
		cout << "Case " << i <<":"<<endl;
		while(cin >> cur){
			if(cur == "End")break;
			scanf("%d %d",&pos,&ad);
			if(cur == "Add") add(pos,ad);
			else if(cur == "Sub") add(pos,-ad);
			else{
				cout << getsum(ad) - getsum(pos - 1) << endl;
			}
		}
	}
}