nn.CrossEntropyLoss()交叉熵损失函数

交叉熵公式

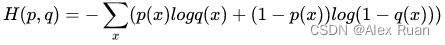
在pytorch中

细究其中CrossEntropyLoss是由softmax+log+NLLLoss组成
那百度一下NLLLoss是什么？

from torch import nn
import torch

# nllloss首先需要初始化
nllloss = nn.NLLLoss() # 可选参数中有 reduction='mean', 'sum', 默认mean
predict = torch.Tensor([[2, 3, 1],
                        [3, 7, 9]])
label = torch.tensor([1, 2])
nllloss(predict, label)
# output: tensor(-6)

nllloss对两个向量的操作为，继续将predict中的向量，在label中对应的index取出，并取负号输出。label中为1，则取2，3，1中的第1位3，label第二位为2，则取出3，7，9的第2位9，将两数取平均后加负号后输出。

个人理解：所以整个过程就是在求每个class下的概率（softmax），然后取log，最后根据公式在目标class下的p是1，其余是0，所以直接把对应的index取出来即可

参考：

NLLLoss:https://zhuanlan.zhihu.com/p/383044774

交叉熵损失函数CrossEntropyLoss()：https://zhuanlan.zhihu.com/p/98785902