G2SAT: Learning to Generate SAT Formulas论文精读

0. Abstract

        SAT（布尔可满足）问题被证明是一个经典的np完全问题，作为一个计算机科学的基本问题，在决策、验证和理论证明等很多方面都有应用。目前的SAT求解器的开发和评估依赖于现有的有限的现实问题，且现有的手工制作的公式由于人类/专家的知识局限性，无法全面地捕获一个SAT实例所具有的广泛特征。这篇文章所提出的G2SAT框架以一组公式为输入，学习SAT公式的生成。文章使用二部图的表示形式对SAT公式进行建模，以图和SAT求解器两种度量展示了其生成的SAT公式的现实的SAT实例的相似性。更重要的是，使用其生成的SAT公式，能够提升现有SAT求解器的求解性能。

1. Introducation

        首先还是对SAT问题的一个背景介绍，说明其作为一个np完全问题，在之前被认为不存在一个统一的方法进行求解。然而随着其在实践上的发展，大规模的SAT问题实例可以被很好地解决，且有一些特定的算法在特定SAT问题上的求解更加高效。例如像WalkSAT这样的不完全搜索策略以及survey propagation等方法对于随机生成的大型SAT问题的求解上具有高效的性能，而使用CDCL的完全搜索策略则在真实的工业环境中的SAT问题的求解更高效。

        接下来讲了SAT公式生成的任务在当前环境下的限制，且伪工业的SAT公式生成被列为了命题推理和搜索的十大关键挑战之一。而对于该问题的解决方法之一，是将原始的公式生成问题重新定义为一个图生成任务。通过一个双射，任意的SAT实例都可以被转化成一个二分图的结构，被称为literal-clause graph（LCG）。先前的手工方法，随着更多的真实SAT实例被发现，其局限性被暴露出来，主要表现为对问题实例的信息捕获能力上的不足。而近年来图生成模型在社交网络、引用关系网络以及化学生物等领域表现出的出色能力给我们提供了一种新的思路。但是由于这些模型没有在二分图方面的限制，所以不能直接运用在该问题上，而后处理的策略也意味着更高的成本，还会丢失掉二部图所具有的一些性质。

        G2SAT作为第一个基于一系列给定公式生成SAT公式的深度生成模型，使用LCG将SAT公式建模为一个二分图生成问题，以下图为例，二分图左边的节点为SAT公式中的变量，右边的节点为SAT公式中的子句（对变量的约束）。任意一个二分图的生成可以看作从一系列的树结构为开始，使用一系列的节点合并操作，在节点合并的同时，树也被合并，从而形成一个二分图。如下图左图所示，从左到右为节点的分割过程，从右到左为节点的合并过程，例如，G3中的橙色节点，在G2种被分割为两个蓝色节点，反之同理。假设我们学习这个合并序列，就可以以一系列的树为起点，以迭代的方式完成真实SAT实例的二分图的构造。这样的每一个迭代步骤作为GCN的一个样本，在每一个迭代中，GCN的权重共享。

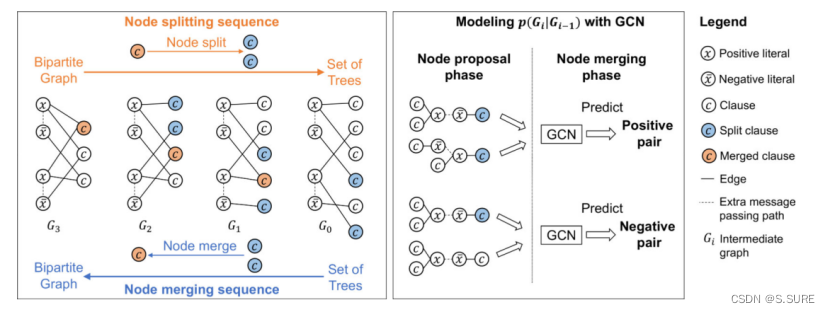
        在上述思路之下，需要考虑如何在只给定静态输入的SAT公式的情况下设计一个顺序生成的过程，即怎样为生成器提供训练样本。如上图左图所示，节点的分割过程可以看作是节点合并的逆过程，因此可以对给定的二分图（真实的SAT实例）执行节点切分的过程，将其分割为一系列的树，然后再反向执行该过程，就实现了一个顺序生成二分图的流程（这样一个正难则反的思路在许多情况下是十分有效的，例如矩阵乘法的张量分解等）。本文训练一个GCN为基础的分类器基于目前生成的图来决定在下一次迭代中，对哪两个节点进行合并。

        在每次迭代中，模型的运行分为两步，第一步随机选择候选节点对，第二步为节点合并阶段，GCN被用于选择最有可能的两个节点执行合并。这样的迭代过程从使用一系列树初始化模型开始，一直到一个用户定义的停止条件结束。

        接下来文章说明了实验结果所表明的模型的优越性，即其在许多具有图特性的SAT实例的SAT公式生成任务上能生成比现有最SOTA的模型更低的误差。且其生成的公式具有与真实SAT实例的公式相同的硬度特性，这是说，对于模型生成的公式，那些用于求解真实SAT问题的求解器表现出的性能要优于解决随机生成的SAT问题的求解器。并且，使用G2SAT生成的公式还可以指导SAT求解器的超参数优化，从而实现更高的性能（更快的求解速度）。

2. Preliminaries

SAT公式生成的目标

        设计一个SAT公式的生成器，输入一系列的SAT公式，生成一个与输入公式具有相似属性的新的SAT公式。这个生成的公式不仅要捕获该SAT实例的图理论的属性，还应捕获其实际的SAT求解器行为的属性。对于这个行为的解释为：对于输入为来自于某个应用领域的公式X，解决该领域SAT实例的求解器也要擅长于求解G2SAT由此生成的SAT公式。

SAT公式和其图表示

        SAT公式由一系列的变量和逻辑运算连接词（与、或、非）构成，当存在一组变量赋值使得整个SAT公式的真值为真时，我们认为该SAT公式对应的问题是可满足的。本文中的SAT公式表示形式为合取范式（CNF），如(x1∨x2∨¬x3)∧(¬x1∨¬x2)，CNF由一系列的子句所构成，子句之间通过与运算连接，每一个子句内部的变量通过或运算连接（因此，一个CNF要为真，要求每个子句的真值为真；而一个子句的真值要为真，只需要其中的任意一个变量的真值为真，这一点是由与运算和或运算的性质所决定的）。对于一个CNF的图表示，文中提到了四种方式：1）字面量-子句图（LCG）：每个字面量和每个CNF子句被表示为一个节点，节点之间的边表示了某个字面量是否在某个子句中出现。边只在变量节点和子句节点之间连接，因此LCG是