算法与数据结构学习笔记（4）：图

线性表中的数据元素叫元素；树中的数据元素叫结点；图中的数据元素叫顶点。

一、图的基本概念（Graph）

（1）定义：由顶点的有穷非空集合和顶点之间边的集合组成。
通常表示为G（V,E），G表示一个图，V表示顶点的集合，E表示边的集合。

1.图的一些概念

• 无向边：若顶点a到b之间的边没有方向，则称这条边为无向边，用（a，b）来表示。

• 无向图：图中任意两个顶点之间的边都是无向边。

• 无向完全图：在无向图中，任意两个顶点之间都存在边。（含有n个顶点的无向完全图有n*（n-1）/2条边）

• 有向边：两顶点之间的边有向，也称为弧。用<a，b>来表示（代表方向是从a到b）。

• 有向图：图中任意两顶点之间的边都是有向边。

• 有向完全图：在有向图中，任意两顶点之间都存在方向互反的两条弧。如下所示
  

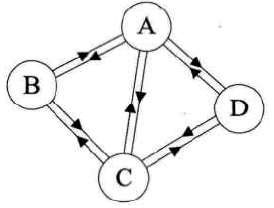
注： 无向边用（），而有向边用<>

• 带权的图称为网。

• 连通图：在无向图中，任意两个顶点之间有路径。

• 连通分量：无向图中的极大（顶点数最多）连通子图称为连通分量。

• 强连通图：在有向图，任意两顶点的a到b和b到a都存在路径（有路径即可，不一定直连）。

• 强连通分量：有向图中的极大强连通子图。

• 连通图的生成树：一个极小的连通子图，它含有图中全部的n个顶点，而且只有n-1条边。
  

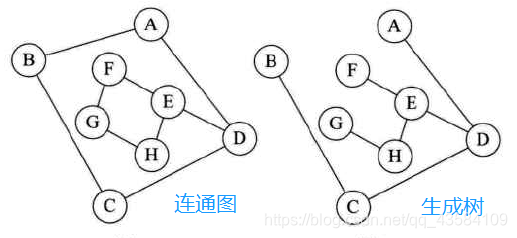
注：
1.有向图中一顶点入度为0，其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。

2.若有一个图有n个顶点和小于n-1条边，则是非连通图。若大于n-1条边，则必定有一个环

3.无向图顶点的边数叫做度，有向图顶点分为入度和出度。

二、图的存储结构

1.邻接矩阵存储

（1）定义：用两个数组来表示图，一个一维数组存储图中的顶点信息。一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。
（2）无向图

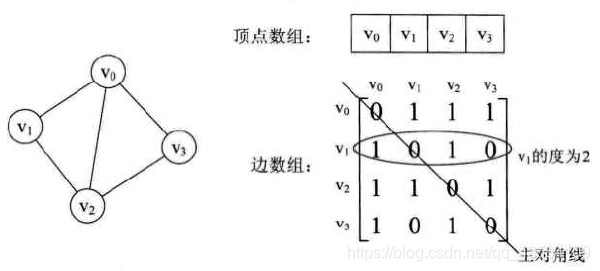
注：
1.无向图的边数组是一个对称矩阵。有向图则不一定。
2.无向图要知道某个顶点的度，其实就是这个顶点Vi在邻接矩阵中第i行（或第i列）的元素之和。v1就为1+0+1+0=2。

（3）有向图

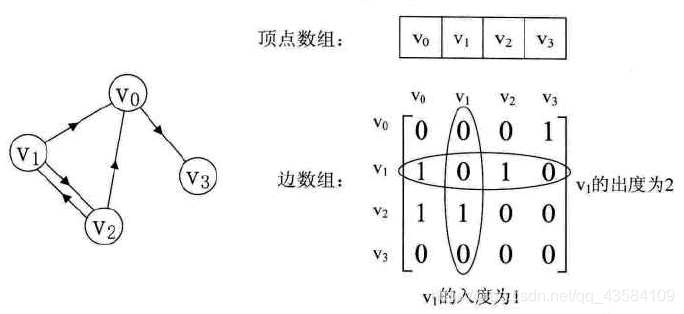
注：
1.有向图的邻接矩阵不一定是对称矩阵。
2.每个顶点的入度是该列各数之和，出度为该行各数之和。

（4）网

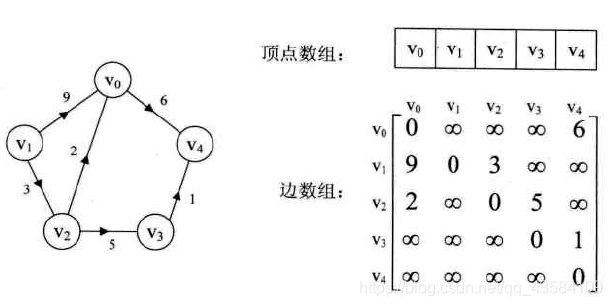
2.邻接表

缺点：对于有向图的邻接表或逆邻接表，出度和入度只能知道一个，要想同时获得出度和入度需要遍历整个图。

（1）定义：
图中顶点用一个一维数组存储，在该数组中，每个数据元素还需要存储指向第一个邻接点的指针（便于查询该顶点的边信息），图中每个顶点的所有邻接点构成一个线性表（用单链存储）。

（2）无向图的邻接表

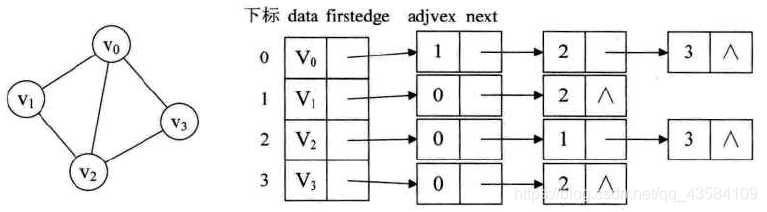
注：
1.顶点表由data（数据域，存储顶点信息）和firstedge（指针域，指向顶点的第一个邻接点）构成。
2.边表由adjvex（邻接点域，存储某顶点的邻接点在顶点表中的下标）和next（存储指向表表中下一个结点的指针）构成。
3.某个顶点的度：这个顶点的边表中结点的个数。
4.两个顶点之间是否有边：测试其中一个顶点的边表中是否有另一个顶点。

（3）有向图的邻接表

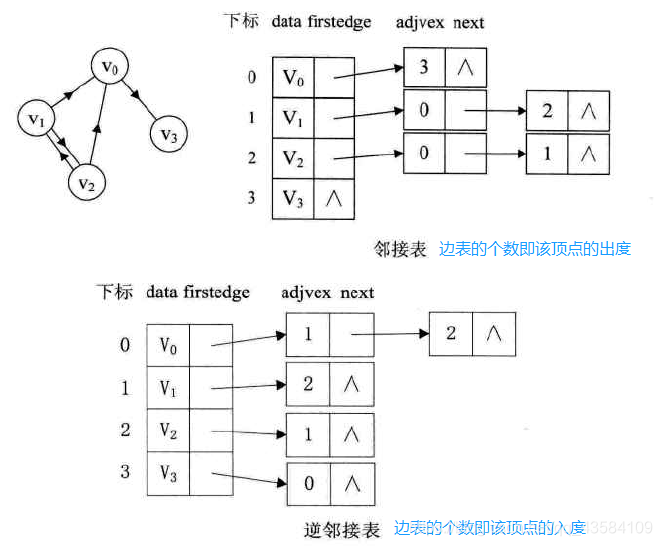
（4）网
网是带有权值的，所以在边表中在增加一个weight的数据域。

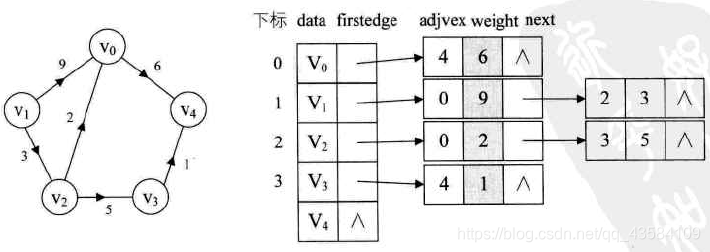
3.十字链表（解决有向图邻接表的缺点）

对于有向图的邻接表或逆邻接表，出度和入度只能知道一个，要想同时获得出度和入度需要遍历整个图。因此，对于有向图，用十字链表（实际就是邻接表+逆邻接表）可以同时得到出度和入度。

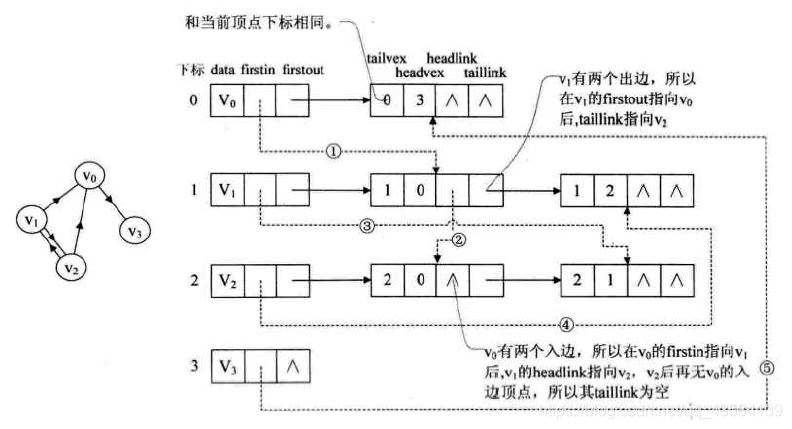
注：
1.顶点表由data、firstin（入边表头指针，指向该顶点的入边表中的第一个结点）和firstout（出边表头指针，指向该顶点的出边表中的第一个结点）构成。

2.边表由tailvex（弧起点在顶点表的下标）、headvex（弧终点在顶点表中的下标）、headlink（入边表指针域，指向终点相同的下一条边）、taillink（边表指针域，指向起点相同的下一条边）

3.实现其实就是邻接表，虚线就是逆邻接表。

4.邻接多重表（解决无向图邻接表的缺点）

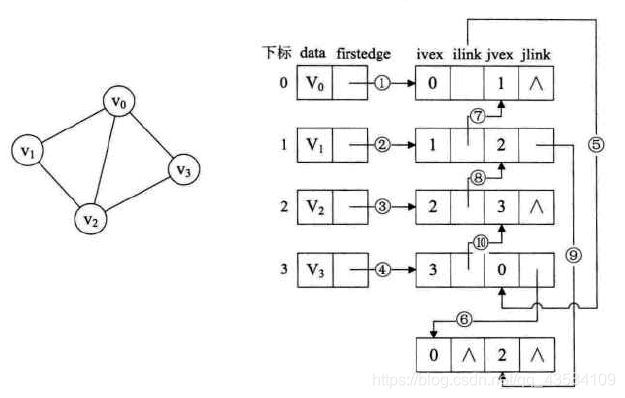
ivex和jvex是与某条边依附的两个顶点在顶点表中的下标。ilink指向依附顶点ivex的下一条边，jlink指向依附顶点jvex的下一条边。

5.边集数组

原理：
由两个一维数组构成。一个用来存储顶点信息，另一个用来存储边的信息（由一条边的起点下标begin，终点下标end，权值weight构成）。

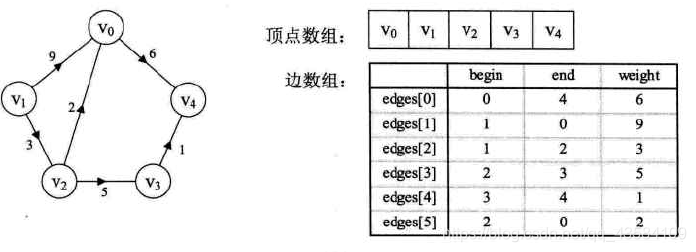
三、图的遍历

1.深度优先遍历

房子里找钥匙挨个房间仔细的找，类似与树的前序遍历
深度优先遍历（Depth_First_Search，简称DFS）又称深度优先搜索。

原理：
1.对于连通图：从图中某个顶点a出发，访问此顶点，然后从a的未被访问的邻接点出发深度优先遍历，直至图中所有和a有路径相同的顶点都被访问到。

2.对于非连通图，先找一个顶点进行一次深度优先比遍历，若图中还有顶点未被访问到，则选择其中一个未被访问的顶点作为起始顶点，重复上述过程，直至图中所有顶点都被访问。

2.广度优先遍历

房子里找钥匙先看每个房间最显眼的位置，然后每个房间再逐渐仔细找，类似与树的层序遍历
广度优先遍历（Breadth_First_Search，简称BFS），又称为广度优先搜索。

3.DFS和BFS的比较

DFS适合目标比较明确，以找到目标为主要目的，BFS则适合在不断扩大遍历范围时找到相对最优解。