时间复杂度和空间复杂度知识点总结

算法：为了解决一个问题，你来写一个解决这个问题的一个方法。也就是一个一系列的计算步骤，用来将输入数据转化为输出结果。

• 那么怎么样才能知道你写的这个算法是好的还是坏的？
  • 时间复杂度和空间复杂度就是衡量一个算法好坏的标准。时间复杂度主要衡量的就是算法的运行速度，而空间复杂度主要衡量的就是一个算法所需要的一个额外空间。

时间复杂度

• 算法的时间复杂度是一个函数基本总的执行次数，也就是一个算法基本语句总的执行次数，关于问题规模n的数学表达式，把这个数学表达式看成算法的时间复杂度一般用f(n)表示。进而分析f(n) 随n的变化情况，这里我们使用大O渐进表示法来求取一个算法的时间复杂度。在实际中一般情况关注的是算法的最坏运行情况，也就是最坏时间复杂度。这样做的原因是：最坏情况下的时间复杂度是一个算法在任何输入实例上运行时间的上界，分析最坏的情况以估算算法指向时间的一个上界。

• 时间复杂度看的是一个算法运行了多长时间，但是为啥最后我的衡量标准不是用时间衡量而是从一个算法基本语句总的执行次数来衡量呢？

  • 因为和环境太相关了。举个例子：假如我们进行一个冒泡排序，算法时间需要十秒。然后同样的代码放到不同的电脑上可能需要5秒。这跟一个叫做cpu主频有关，你的主频越高，你执行指令的速度就越快。

时间复杂度的分析方法：

1、时间复杂度就是一个算法基本语句总的执行次数，关于问题规模n的数学表达式。
2、一般默认的就是最坏的时间复杂度，就是分析一个算法在最坏的情况下执行的次数
例如在一个数组中找一个数字是否存在:最坏的情况就是把整个数组都遍历一遍，然后才找到那个元素，
这个就是这个算法在最坏的情况下执行的次数。
3、如果算法执行的次数是一个常数，就用O（1）表示，如果还有其它项就忽略掉常数项。
4、我们要关注运行时间的增长趋势，关注函数式中整体增长最快的一个表达式来作为保留最高阶项的依据，然后最高阶项的系数化为1。
5、计算时间复杂度是估算随着n的增长函数执行次数的增长趋势。
6、递归算法的时间复杂度为:递归的总次数每次递归中基本操作所执行的次数。

常见的时间复杂度有以下七种，算法的时间复杂度依次增加：O(1)常数型、O(log2^n)对数型、O(n)线性型、 O(nlog2 ^n）二维型、O(n ^2)平方型，O(n ^3)立方型、O(2 ^n)指数型。

空间复杂度

算法的空间复杂度就是一个算法在运行过程中临时占用存储空间大小的量度。并不是计算实际占用的空间，而是计算整个算法的辅助空间，与问题的规模没有关系。空间复杂度的计算跟时间复杂度的计算规则基本一样，也是用大O渐进表示法。

• 递归算法的空间复杂度：递归深度N*每次递归所要的辅助空间。如果每次递归所需的辅助空间是常数，则递归的空间复杂度就是O（n）。

//计算二分查找的时间复杂度和空间复杂度
int BinarySearch(int* arr, int sz, int n) {
 assert(arr);
 int left = 0;
 int right = sz - 1;
 while (left <= right) {
  int mid = left + (right - left) / 2;
  if (arr[mid] < n) {
   left = mid + 1;
  } else if (arr[mid] > n) {
   right = mid - 1;
  } else {
   return mid;
  }
 }
 return -1;
}

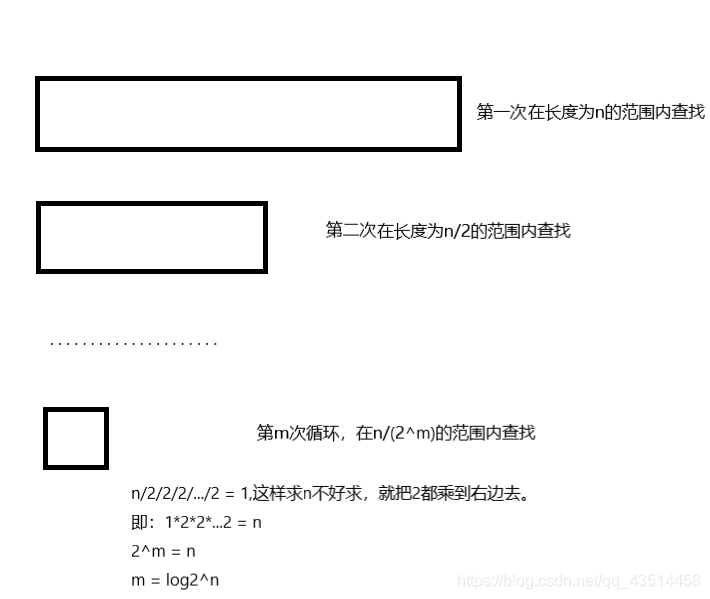
所以二分查找的时间复杂度就为O(log2^n)。由于二分查找开辟了常数个辅助空间，所以二分查找的空间复杂度就为O(1);

//计算Fibonacci的空间复杂度和时间复杂度（非递归）
long long* Fibonacci(size_t n) {
 if (n == 0) {
  return NULL;
 }
 long long* fibArray = new long long[n + 1];//动态开辟了n+1个空间
 fibArray[0] = 0;
 fibArray[1] = 1;
 for (int i = 2; i <= n; ++i) {
  fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
 }
 return fibArray;
}

时间复杂度： for (int i = 2; i <= n; ++i)循环次数为n-1次，所以时间复杂度为O(n);
空间复杂度：n和i都是开辟了常数个空间，里面还有动态开辟了n+1个空间，所以空间复杂度为O(n)；

//计算Fibonacci的时间复杂度和空间复杂度（递归）
long long Fib(int n){
	if(n<3){
	  return 1;
	}else{
	   return Fib(n-1)+fib(n-2);
	}
}

时间复杂度：

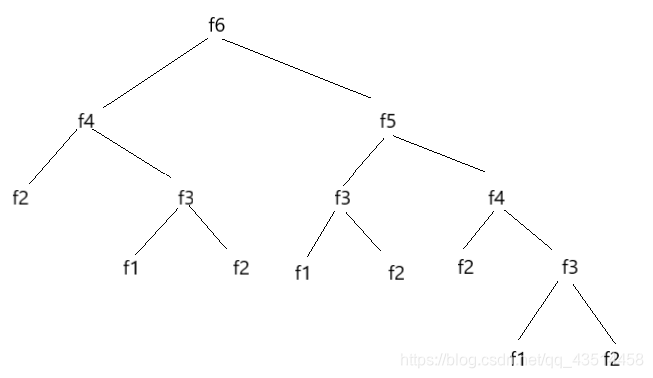
计算时间复杂度就是就是单次递归函数中执行次数*递归函数总的递归次数。计算上图的时间复杂度就是把他们每一层执行了多少次加起来，由于直接相加不好算，我们就把最后一层的两个结点放到上一层上，即2^0+2 ^1+…+2 ^n-3 = 2 ^n-4,所以时间复杂度就为O(2 ^n)。
空间复杂度O(n)。
对Fibonacci优化之后的时间复杂度和空间复杂度

long long Fib(long long first,long long second){
 if(n<3){
   return 1;//单次需要执行1次
 }else{
    return Fib(second,first+second,n-1);
 }
}

时间复杂度O(n);
空间复杂度：单次递归需要用到的空间*递归的深度，这个空间复杂度就是O(1)，即直接在一个空间里修改。