二叉搜索树
基本概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 它的左右子树也分别为二叉排序树。
如下图所示
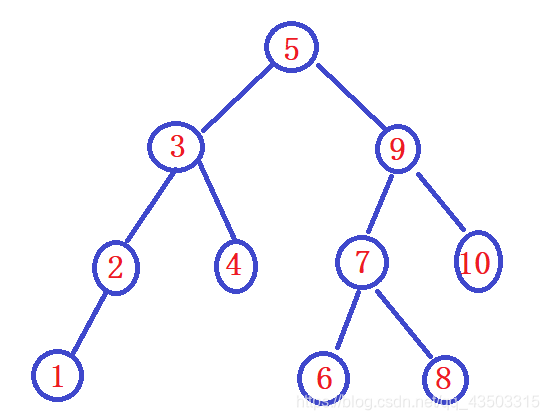
二叉搜索树的查找
- 若根节点 = 要查找的节点 返回true
- 若根节点 < 要查找的节点 ,在右子树种查找
- 若根节点 > 要查找的节点 ,在左子树中查找
重复上述过程,直至查找成功返回找到的结点,否则返回false。
二叉搜索树的插入
- 若二叉搜索树为空,直接插入
- 若二叉搜索树不为空,按二叉搜索树性质查找插入位置,插入新节点
二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程如下:
情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点
情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点
情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题
二叉搜索树的实现
//实现简易版的二叉搜索树
// 插入 查找 删除
#include <iostream>
using namespace std;
template <class k,class v>
class BSTreeNode {
public:
BSTreeNode(const pair<k, v> kv)
:_kv(kv)
, left(nullptr)
, right(nullptr)
{}
public:
pair<k, v> _kv;
BSTreeNode<k, v>* left;
BSTreeNode<k, v>* right;
};
template<class k,class v>
class BSTree {
public:
typedef BSTreeNode<k,v> Node;
BSTree()
:_root(nullptr)
{}
//插入
bool Insert(const pair<k, v> kv) {
if (_root == nullptr) {
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->left;
}
else {
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first) {
parent->right = cur;
}
else {
parent->left = cur;
}
return true;
}
//查找
Node* Find(const k& key) {
Node* cur = _root;
while (cur) {
if (cur->_kv.first < key) {
cur = cur->left;
}
else if(cur->_kv.first > key){
cur = cur->right;
}
else{
return cur;
}
}
return nullptr;
}
//删除
bool Remove(const k& key) {
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < key) {
parent = cur;
cur = cur->right;
}
else if(cur->_kv.first > key){
parent = cur;
cur = cur->left;
}
else { //找到
//没有孩子,只有一个孩子,两个孩子都有
Node* del = cur;
//只有右孩子
if (cur->left == nullptr) {
if (parent == nullptr) {
_root = cur->right;
}
else{
if (parent->left == cur) {
parent->left = cur->right;
}
else {
parent->right = cur->right;
}
}
}
//只有左孩子
else if (cur->right == nullptr) {
if (parent->left == cur) {
parent->left = cur->left;
}
else {
parent->right = cur->left;
}
}
//左右孩子都有
else {
Node* reparent = cur;
Node* replace = cur->right;
while (replace->left) { //在右子树中找最左节点
reparent = replace;
replace = replace->left;
}
cur->_kv = replace->_kv; //替换节点值
del = replace;
if (reparent->left == replace) {
reparent->left = replace->right;
}
else {
reparent->right = replace->right;
}
}
delete del;
return true;
}
}
return false;
}
//中序遍历
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->left);
cout << root->_kv.first << " ";
_InOrder(root->right);
}
private:
Node* _root;
};
void TestBSTree1()
{
BSTree<int, int> tree;
tree.Insert(make_pair(1, 1));
tree.Insert(make_pair(3, 1));
tree.Insert(make_pair(4, 1));
tree.Insert(make_pair(6, 1));
tree.Insert(make_pair(1, 1));
tree.Insert(make_pair(2, 1));
tree.InOrder();
tree.Remove(1);
tree.Remove(3);
tree.Remove(2);
tree.Remove(6);
tree.Remove(4);
tree.Remove(1);
tree.Remove(10);
tree.InOrder();
}
int main(void) {
TestBSTree1();
system("pause");
return 0;
}
二叉搜索树性能分析
我们可以看出来其实它就是一个二分查找,所以BST的查找和插入删除关键字的速度较于一般的数组链表都比较快。这就是BST产生的原因。但是,创建好BST后,插入数据的随机性,所以会出现比较极端的BST。
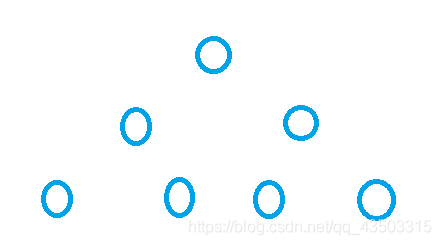
最优情况下,二叉搜索树为完全二叉树,其时间复杂度为:log(n)

最差情况下,二叉搜索树退化为单支树,其时间复杂度为:O(n)
第一张图的就是我们理想的情况,可是却可能出现第二张图的情况,第一张图操作的时间复杂度为log(n),而第二张图则为O(n),所以这也是BST没有广泛使用的原因。





















 298
298

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








