【POJ - 2676】Sudoku（数独 dfs+回溯）

最新推荐文章于 2025-12-03 13:56:23 发布

原创最新推荐文章于 2025-12-03 13:56:23 发布 · 56 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#深度优先 #算法

本文介绍了一种使用深度优先搜索(DFS)和回溯法解决数独问题的算法。通过枚举1到9的数字并利用三个数组进行标记来实现每行、每列和每个3x3子网格内的数字不重复的约束条件。

-->Sudoku

直接中文

Descriptions:

Sudoku对数独非常感兴趣，今天他在书上看到了几道数独题:
给定一个由3*3的方块分割而成的9*9的表格(如图)，其中一些表格填有1-9的数字，其余的则为空白(数字0为空白)。请在空白表格中填入数字1-9使得9*9表格的每行、每列、每个3*3块内无重复数字。

Input

第一行输入一个整数T，表示样例数量。对于每个样例, 一共9行, 表示数独表格的每一行。接下来每一行输入一个字符串表示数独表格的每一行的9个数字。数独表格中空白用数字0表示。

Output

对于每组样例，输出完整的数独表格，即数独表格的每一个空白都按规定填满数字。如果答案不唯一，输出任何一个答案就行。

Sample Input

Sample Output

提示可能会有多组解，输出其中一种即可。

题目链接:

https://vjudge.net/problem/POJ-2676

1~9 一个一个枚举

dfs试探，失败则回溯

用三个数组进行标记每行、每列、每个子网格已用的数字，用于剪枝

bool row[10][10]; //row[i][x] 标记在第i行中数字x是否出现了

bool col[10][10]; //col[j][y] 标记在第j列中数字y是否出现了

bool grid[10][10]; //grid[k][x] 标记在第k个3*3子格中数字z是否出现了

row 和 col的标记比较好处理，关键是找出grid子网格的序号与行i列j的关系

即要知道第i行j列的数字是属于哪个子网格的

首先我们假设子网格的序号如下编排：

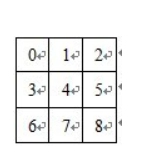
由于1<=i、j<=9，我们有： (其中“/”是C++中对整数的除法)

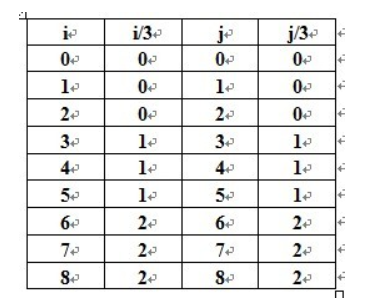
令a= i/3 , b= j/3 ，根据九宫格的行列与子网格的关系，我们有:

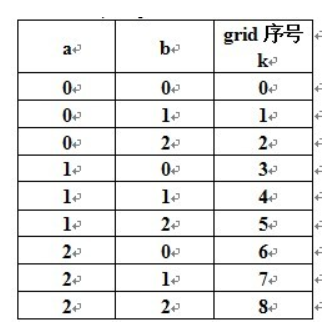
不难发现 3a+b=k

即 3*(i/3)+j/3=k

又我在程序中使用的数组下标为 1~9，grid编号也为1~9

因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k
以上论述转自https://blog.youkuaiyun.com/lyy289065406/article/details/6647977

AC代码：

#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
#include <sstream>
#define mod 1000000007
#define eps 1e-6
#define ll long long
#define INF 0x3f3f3f3f
#define MEM(x,y) memset(x,y,sizeof(x))
#define Maxn 15
using namespace std;
int result;
int T,h,w;
int mp[Maxn][Maxn];//地图
bool row[Maxn][Maxn];//row[i][x]  标记在第i行中数字x是否出现了
bool col[Maxn][Maxn];//col[j][y]  标记在第j列中数字y是否出现了
bool grid[Maxn][Maxn];//grid[k][x] 标记在第k个3*3子格中数字z是否出现了
int dfs(int x,int y)
{
    if(x==10)
        return 1;
    int f=0;
    if(mp[x][y])
    {
        if(y==9)
            f=dfs(x+1,1);
        else
            f=dfs(x,y+1);
        if(f)//回溯
            return 1;
        else
            return 0;
    }
    else
    {
        int k=3*((x-1)/3)+(y-1)/3+1;
        for(int i=1; i<=9; i++)//枚举1~9填空
            if(!row[x][i]&&!col[y][i]&&!grid[k][i])
            {
                mp[x][y]=i;
                row[x][i]=1;
                col[y][i]=1;
                grid[k][i]=1;
                if(y==9)
                    f=dfs(x+1,1);
                else
                    f=dfs(x,y+1);
                if(!f)//回溯，继续枚举
                {
                    mp[x][y]=0;
                    row[x][i]=0;
                    col[y][i]=0;
                    grid[k][i]=0;
                }
                else
                    return 1;
            }
    }
    return 0;
}
int main()
{
    int h=w=9;
    cin>>T;
    while(T--)
    {
        MEM(row,0);
        MEM(col,0);
        MEM(grid,0);
        for(int i=1; i<=h; i++)
            for(int j=1; j<=w; j++)
            {
                char ch;//注意，这里一定要用char类型，不然读不进去
                cin>>ch;
                mp[i][j]=ch-'0';
                if(mp[i][j])
                {
                    int k=3*((i-1)/3)+(j-1)/3+1;
                    row[i][mp[i][j]]=1;
                    col[j][mp[i][j]]=1;
                    grid[k][mp[i][j]]=1;
                }
            }
        //从(1,1)开始搜索
        dfs(1,1);
        //输出
        for(int i=1; i<=h; i++)
        {
            for(int j=1; j<=w; j++)
                cout<<mp[i][j];
            cout<<endl;
        }
    }
}