贪心法经典例题

最新推荐文章于 2022-06-10 09:32:24 发布

原创最新推荐文章于 2022-06-10 09:32:24 发布 · 348 阅读

2 ·

CC 4.0 BY-SA版权

地图上我们的距离只有三厘米专栏收录该内容

24 篇文章

订阅专栏

有1元，5元，10元，50元，100元，500元的硬币各C1，C5，C10，C50，C500枚。现在要用这些硬币支付A元，最少需要多少枚硬币？
输入：
3 2 1 3 0 2
620
输出：
6

#include <iostream>
using namespace std;
int main()
{
	int c[6];
	const int v[6] = {1, 5, 10, 50, 100, 500};
	for (int i = 0; i < 6; i++)
	{
		cin >> c[i];
	}
	int A;
	cin >> A;
	int ans = 0;
	for (int i = 5; i >= 0; i--)
	{
		int t = min(A / v[i], c[i]);
		A -= t * v[i];
		ans += t;
	}
	cout << ans;
	return 0;
}

有n项工作，每项工作分别在s;时间开始，在t时间结束。对于每项工作，你都可以选择参与与否。如果选择了参与，那么自始至终都必须全程参与。此外，参与工作的时间段不能重叠(即使是开始的瞬间和结束的瞬间的重叠也是不允许的)

输入：
5
1 2 4 6 8
3 5 7 9 10
输出：
3
分析：这个问题也是贪心（废话，放在贪心这一节里面），但不像前面硬币那么简单。书上解释很清楚，这里不多说，也不做过多详细证明（因为不想打字，而且我也不会。。。），下面给出方法和简要证明。
结束时间越早，之后可选择的工作越多，因此本题思路是：在可选的工作中，每次都选取结束时间最早的工作。
看书本上说，证明很复杂，但是可以按照下面方法证明：
① 与其他方案相比，该算法的选择方案在选取了相同数量的更早开始的工作时，其最终结束时间
不会比其他方案的更晚。
② 所以，不存在选取更多工作的方案。

#include <iostream>
#include <algorithm>
using namespace std;
int Start[1005], End[1005];
pair<int, int> node[1005];
int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> Start[i];
	}
	for (int i = 0; i < n; i++)
	{
		cin >> End[i];
	}
	for (int i = 0; i < n; i++)
	{
		node[i].first = End[i];
		node[i].second = Start[i];
	}
	sort(node, node + n);
	int ans = 0, t = 0;//t为结束时间 
	for (int i = 0; i < n; i++)
	{
		if (t < node[i].second)
		{
			t = node[i].first;
			ans++;
		}
	}
	cout << ans << endl;
	return 0;
}

给定长度为N的字符串S，要构造一个长度为N的字符串T，起初，T是一个空串，随后反复进行下列任意操作。
① 从S的头部删除一个字符，添加到T的尾部；
② 从S的尾部删除一个字符，添加到T的尾部；
目标是要构造字典序尽可能小的字符串T。

分析：从字典序顺序上看，无论T末尾多大，只要前面部分较小就行。所以只需不断取S开头和末尾较小的一个字符放到T的末尾。

#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
int main()
{
	int n;
	cin >> n;
	string s, s1, t;//s1为反转字符 
	cin >> s;
	s1 = s;
	reverse(s1.begin(), s1.end());
	int i = 0;
	while (s.length() != 0)
	{
		if (s < s1)
		{
			t.push_back(s[0]);
			s = s.substr(1, s.length() - 1);
		}
		else
		{
			t.push_back(s[s.length() - 1]);
			s = s.substr(0, s.length() - 1);
		}
		s1 = s;
		reverse(s1.begin(), s1.end());
	}
	cout << t << endl;
	return 0;
}

一个直线上有N个点。点i的距离是Xi。从这些点中选取若干个加上标记。要求：对于每个点，与其距离为R的范围内必有做标记的点（包括自身）。求至少标记多少点才能满足要求。
戳这->原题POJ3069
分析：显然我们应该从最左边开始考虑，对于这个点，距离其R以内的区域必须要有带标记的点。因此，带标记的点一定在次点的右侧（包含这个店本身）。我们只需要在它的右侧找到距离左端第一个点的距离刚好小于或等于R（再往右就大于R），记这个点为s，那么下一个标记的点p就是在s的右侧距离s的距离刚好小于或等于R，反复执行该过程。

#include <iostream>
using namespace std;
int a[10005];
int main()
{
	#int n, r;
	cin >> n >> r;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	int i = 0, ans = 0;
	while (i < r)
	{
		int s = a[i++]; 
		//一直向右前进直到遇到距离s大于r的点 
		while (i < r && a[i] <= s + r)
		{
			i++;
		}
		int p = a[i - 1];
		//一直向右前进直到遇到距离p大于r的点 
		while (i < r && a[i] <= s + p)
		{
			i++;
		}
		ans++;
	}
	cout << ans << endl;
	return 0;
}

有一个农夫要把一个木板钜成几块给定长度的小木板，每次锯都要收取一定费用，这个费用就是当前锯的这个木版的长度，给定各个要求的小木板的长度，及小木板的个数n，求最小费用。戳这->原题POJ3253
提示：
以
3
8 8 5为例：
先从无限长的木板上锯下长度为 21 的木板，花费 21
再从长度为21的木板上锯下长度为5的木板，花费5
再从长度为16的木板上锯下长度为8的木板，花费8
总花费 = 21+5+8 =34

分析：切割方法对应如下二叉树，这里每个叶子节点就对应切割出的一块块木板，叶子结点深度就对应所需切割次数，，开销合计就是各叶子结点的木板长度 x 节点深度。
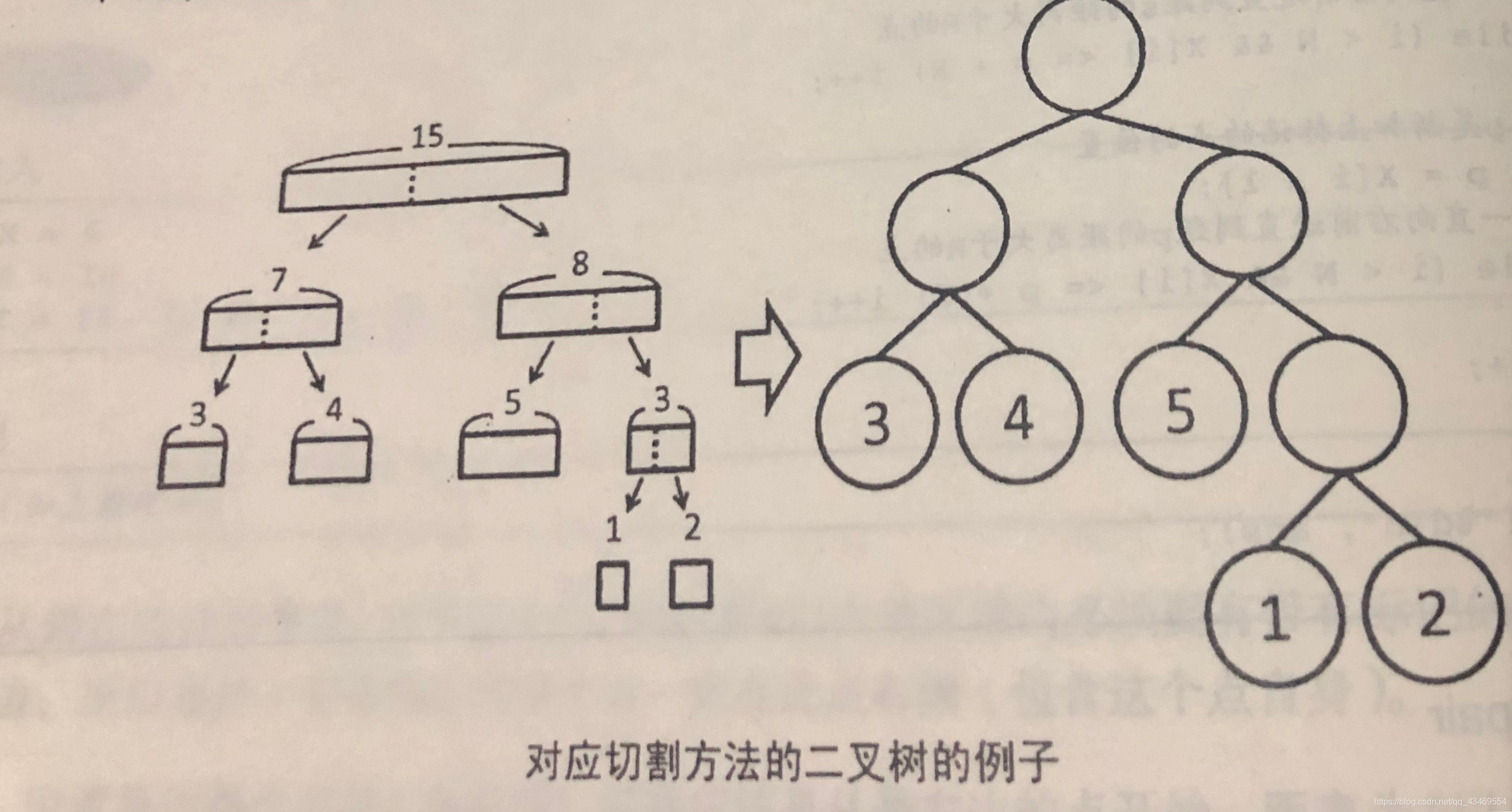
在这里插入图片描述
这题其实是哈夫曼思想，要使总费用最小，那么每次只选取最小长度的两块木板相加，再把这些和累加到总费用中即可。这题可用优先队列来做。

#include <iostream>
#include <queue>
using namespace std;
int main()
{
	int n;
	cin >> n;
	priority_queue<long long, vector<long long>, greater<long long> > q;
	while (n--)
	{
		long long x; 
		cin >> x;
		q.push(x);
	} 
	long long ans = 0;
	while (!q.empty())
	{
		long long m1 = q.top();
		q.pop();
		long long m2 = q.top();
		q.pop();
		ans += m1 + m2;
		if (q.empty())
		{
			break;
		}
		q.push(m1 + m2);
	} 
	cout << ans << endl;
	return 0;
}