归并排序——归并、两路归并递归及非递归

9.5 归并排序

9.5.1 归并

1. 所谓归并，就是将两个或两个以上的有序表合并成一个新的有序表。有两个已经排好序的有序表A[1]~ A[n]和 B[1]~ B[m]通过归并把它们合成一个有序表C[1]~C[m+n]。这种归并方法称为两路归并。
2. 其基本思想是：设有两个有序表A和B，其数据元素个数（表长）分别为n和m，变最i和j 分别是表A和表B的当前检测指针；设表C是归并后的新有序表，变量k是它的当前存放指针。
   开始时i、j、k都分别指向A、B、C三个表的起始位置；然后根据A[i]与B[i]的关键字的大小，把关键字小的数据元素放到新表C[k]；且相应的检测指针（i或j）和存放指针k增加1。如此循环，当i与j中有一个已经超出表长时，将另一个表中的剩余部分照抄到新表C[k]~C[m+n]中·。
   
3. 两路归并算法：
   两个待归并的有序表省首尾相接存放在数组elem[]中，其中第一个表的下标范围是从low到 mid，另一个表的下标范围从 mid+1 到 high。
   前一个表中有 mid-low+1个数据元素，后一个表中有high-mid 个数据元素。归并时新有序表先存放在一个辅助数组tmpElem[]中，完成归并后再把tmpElem[]中元素放回数组elem[]中。
4. 代码实现

template<class ElemType> void Merge(ElemType elem[],int low,int mid,int high)
{
    ElemType *tmpElem=new ElemType[high+1];//定义临时数组
    int i=low,j=mid+1,k=low;
    //i为归并时前一表当前元素的下标,j为归并后一表当前元素的下标,
    //k为tmpElem中当前元素的下标
    while(i<=mid && j<=high)
        if(elem[i]<=elem[j])
            tmpElem[k++]=elem[i++];
        else
            tmpElem[k++]=elem[j++];
    while(i<=mid)//归并elem[low..mid]中剩余元素
        tmpElem[k++]=elem[i++];
    while(j<=high)//归并elem[mid+1..high]中剩余元素
        tmpElem[k++]=elem[j++];
    for(i=low;i<=high;i++)//将tmpElem复制回elem
        elem[i]=tmpElem[i];
    delete [] tmpElem;
}

在上述算法中，所有数据元素都将被移入辅助数组 tmpElem[]中。所以，总的数据元素移动次数为（mid-low+1）+（high-mid）=high-low+1；在 while循环中，每进行一次关键字的比较，就有一个数据元素被移入辅助数组 tmpElem[]，而在 while循环后面数据元素不进行比较直接被移入辅助数组 tmpElem[]中。所以，在算法实现时关键字比较次数不会超过数据元素的移动次数。

9.5.2 两路归并排序

1. 两路归并排序（merge sort）就是利用两路归并算法进行排序。
2. 其算法基本思想是：
   假设初始数据表有n个数据元素，首先把它看成是长度为1的首尾相接的n个有序子表（以后称它们为归并项），先做两两归并，得⌈n/2⌉个长度为2的归并项（如果n为奇数，则最后一个归并项的长度为1）；再做两两归并……如此重复，最后得到一个长度为n的有序序列。两路归并排序由多趟归并过程实现。第一趟令归并项的长度为len=1，以后每执行一趟后将len加倍。
3. 下面先讨论一趟归并的情形：设数组elem[0]到elem[n-1]中的n个数据元素已经分为一些长度为len的归并项，将这些归并项两两归并，归并成一些长度为2len 的归并项。如果n不是2len的整数倍，则一趟归并到最后，可能遇到以下两种情形。
   1）剩下一个长度为len 的归并项和另一个长度不足len的归并项，可用一次 merge算法，将它们归并成一个长度小于2*len的归并项。
   2）只剩下一个归并项，其长度小于或等于 len，此时就不需要进行归并了。

template<class ElemType> void MergeSort(ElemType elem[],int n)
{
    int len=1,i;
    while(len<n)
    {
        i=0;
        while(i+2*len<=n)
        {
            //对从i开始的长度为len的两个相邻有序区间进行归并
            Merge(elem,i,i+len-1,i+2*len-1);
            i+=2*len;
        }
        if(i+len<n)//对最后两个相邻有序区间进行归并
            Merge(elem,i,i+len-1,n-1);
        len*=2;
    }
}

4. 在两路归并排序算法中要调用Merge()函数⌈n/(2len)⌉次，而每次 Merge()要执行比较次数不超过 2len-1，函数 MergeSort()调用Merge()正好⌈log2n⌉ 次，所以两路归并排序算法总的时间复度为O(nlog2n)。
5. 两路归并排序占用附加存储较多，需要另外一个与原待排序数据元素数组同样大小的辅助数组（辅助数组存放的是归并完成后的数据，在把辅助数组复制到原数组之前，原数组存放的是未经归并的数据），所以其空间复杂度为O（n）。
6. 在两路归并排算法中，每一趟归并都是相邻的归并项进行两路归并，因此对于两个关键字相同的数据元素，它能够保证原来在前面的数据元素在排序后仍然在前面。所以，两路归并排序是一个稳定的排序方法。

9.5.3 递归的归并排序

1. 在递归的归并排序方法中，首先要把整个数据表划分为长度大致相等的左右两个部分，分别称为左子表和右子表，对这两个子表分别进行归并排序（递归），然后再把已排好序的这两个子表进行两路归并，得到一个有序表。
   
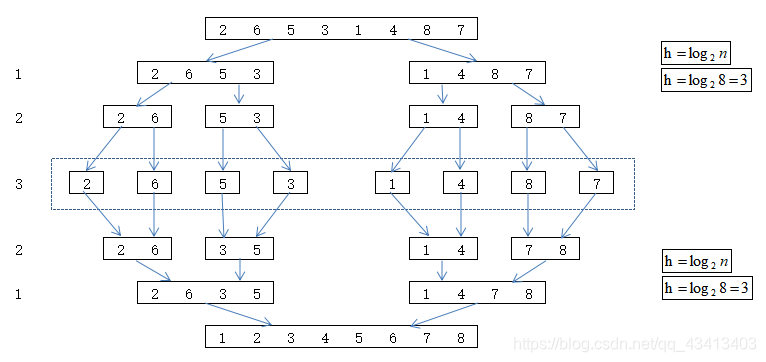
   过程可以参看上图。
2. 代码实现
   （1）顺序表上实现

template<class ElemType> void RecursionMergeSort(ElemType elem[],int low,int high,int n)
{
    if(low<high)
    {
        int mid=(low+high)/2;
        //将elem[low..high]平分为elem[low..mid],elem[mid+1..high]
        RecursionMergeSort(elem,low,mid,n);
        RecursionMergeSort(elem,mid+1,high,n);
        Merge(elem,low,mid,high);
        //对elem[low..mid],elem[mid+1..high]进行归并
    }
}

（2）链表实现
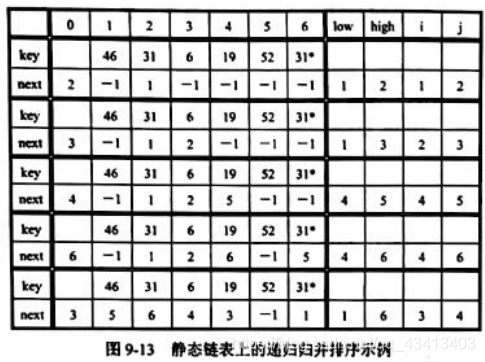
①在此数据表以静态链表存储，设待排序的数据元素存放在静态链表elem中。初始时，置所有的elem[i].next=-1，1<=i<=n （（n为表长），即每个链表结点都是一个独立的单链表。elem[0]用于表示结果链表的头结点。
②函数 linkListMergc()是将两个有序的单链表归并成一个有序单链表的算法，其中p和q分别是参加归并的两个单链表的头指针。
③有一点希望注意的是，为了便于实现递归返回后的逐层归并，函数 linkListMerge()返回结果链表的第一个数据元素结点的指针(elem[0].next)，结果链表中数据元素按关键字递增顺序排列。

template<class ElemType> int LinkListMerge(Node<ElemType> elem[],int p,int q)
{
    //p和q为表头指针的有序链表归并
    int k=0;//k为结果链表的头节点指针
    while(p!=-1 && q!=-1)
        if(elem[p].data<=elem[q].data)
        {
            elem[k].next=p;
            k=p;
            p=elem[p].next;
        }
        else
        {
            elem[k].next=q;
            k=q
              q=elem[q].next;
        }
    if(p==-1)
        elem[k].next=q;
    else
        elem[k].next=p;
    return elem[0].next;
}
template<class ElemType> int LinkListMergeSort(Node<ElemType> elem[],int low,int high)
{
    if(low>=high)
        return low;
    int mid=(low+high)/2,p,q;
    p=LinkListMergeSort(elem,low,mid);
    q=LinkListMergeSort(elem,mid+1,high);
    return LinkListMerge(elem,p,q);
}

外部调用静态链表的递归归并排序函数的形式为LinkListMergeSot (elem,1,n);
④在静态链表上实现的递归归并排序算法，通过链接指针的修改以实现数据元素接点的逻辑有序链接，因此不需要数据元素移动。计算时间可以用数据元素关键字的比较次数来测量。算法的递归深度为O(log2n)，所以总的时间复杂度为O(nlog2n)，它也是一种稳定的排序方法。

总结

1. 归并

• 总的数据元素移动次数为(mid-low+1)+(high-mid)=high-low+1
• 关键字比较次数不会超过数据元素的移动次数。
• 辅助数组 tmpElem[n+m]

2. 二路归并排序

• 有n个数据元素，首先把它看成n个长度为1的归并项，做两两归并len*=2，得⌈n/2⌉个长度为2的归并项，直到最后得到一个长度为n的有序序列。
• 调用Merge()函数⌈n/(2len)⌉次（执行比较次数不超过 2len-1），函数 MergeSort()调用Merge()正好⌈log2n⌉ 次，所以两路归并排序算法总的时间复度为O(nlog2n)
• 空间复杂度为O(n)，辅助数组长度n
• 稳定

3. 递归的归并排序

• 首先把整个数据表划分为长度大致相等的左右两个部分，对这两个子表分别进行归并排序（递归），然后再把已排好序的这两个子表进行两路归并，得到一个有序表。
• 算法的递归深度为O(log2n)，所以总的时间复杂度为O(nlog2n)
• 稳定

其他

1. 两个链表的交集和并集（无论有序还是无序），要求不开辟新的空间
   转载自：https://blog.youkuaiyun.com/taoyc888888/article/details/98608915

///链表基本操作
#include<stdio.h>
#include<stdlib.h>
typedef struct LNode{
	int data;
	struct LNode* next;
}LNode;
LNode* Createlist(int length)//尾插法建立链表 
{
	LNode* L=(LNode*)malloc(sizeof(LNode));
	L->next=NULL;
	LNode* p=L;
	for(int i=0;i<length;i++)
	{
		LNode* t=(LNode*)malloc(sizeof(LNode));
		t->next=NULL;
		scanf("%d",&t->data);
		p->next=t;
		p=t;
	}
	return L;
}
void scan(LNode* L)
{
	LNode* p=L->next;
	while(p)
	{
		printf("%d ",p->data);
		p=p->next;
	}
	printf("\n");
}

///交集
LNode* merge(LNode* la,LNode* lb)
{
	LNode *pa=la->next;
	LNode *pb=lb->next;	
	LNode* q=lb;
	LNode* t;
	la->next=NULL;
	while(pa)
	{
		while(pb)
		{
			if(pb->data==pa->data)
			{
				 
				t=pb;
				pb=pb->next;
				t->next=la->next;
				la->next=t;
				q->next=pb;
			}
			else
			{
			pb=pb->next;
			q=q->next;	
			 } 
		}
		pa=pa->next;
		pb=lb->next;
		q=lb;		
	}
	return la;
}

///并集
LNode* combine(LNode* la,LNode* lb)
{
	LNode* pb=lb->next;
	LNode* t;
	int e;
	while(pb)
	{
		LNode* pa=la->next;		
		int i=0;
		while(pa)
		{
			e=pb->data;
			if(e==pa->data) i=1;//用i标记遍历一遍之后是否存在
			pa=pa->next;
		}
		if(i==0)
		{
			t=pb;
			pb=pb->next;
			t->next=la->next;
			la->next=t;
		}
		else pb=pb->next;//若存在，则不插入
		
	}
	return la;
}