【数据分析】02 - numpy
文章目录
https://numpy.org/numpy-tutorials/
https://numpy.org/doc/stable/
一:numpy概述
numpy -> 开源的python科学计算库 -> 对数组和矩阵进行计算
numpy中包含了线性代数,傅里叶变换、随机数生成等大量函数
对于同样的数值计算任务,使用Numpyb比直接Python代码实现,优点:
- 代码更简洁:Numpy直接以数组、矩阵为粒度计算并且支撑大量的数学函数,而python需要用for循环从底层实现;
- 性能更高效:Numpyl的数组存储效率和输入输出计算性能,比Python使用List或者嵌套List好很多;
- 注:Numpy的数据存储和Python原生的List是不一样的
- 注:Numpy的大部分代码都是语言实现的,这是Numpyl比纯Python代码高效的原因
Numpy是Python各种数据科学类库的基础库 -> 比如:Scipy, Scikit-Learn、TensorFlow, pandas等
二:创建数组
NumPy定义了一个n维数组对象,简称ndarray对象,它是一个一系列相同类型元素组成的数组集令。
数组中的每个元素都占有大小相同的内存块
ndarray对象采用了数组的索引机制,将数组中的每个元素映射到内存块上,并且按照一定的布局对内存块进行排列
numpy数组 vs python的数组
- NumPy 数组更紧凑,存储效率更高
- 向量化操作,无需显式循环
- 底层用 C 实现,运算速度更快
- 丰富的数学函数和线性代数运算
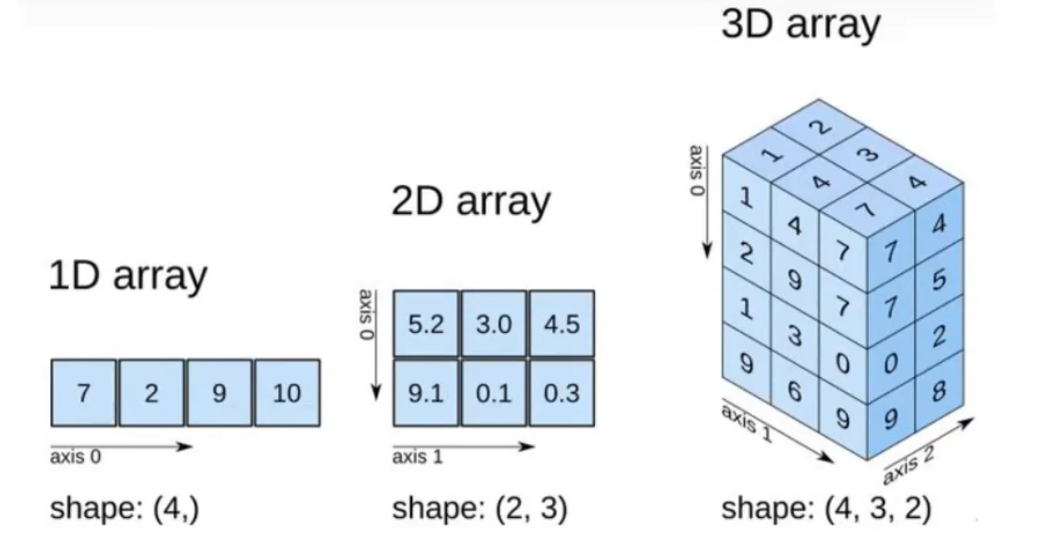
每一个numpy数组有如下的5个属性
arr = np.array([[1, 2, 3], [4, 5, 6]])
print(arr.ndim) # 维度数 (2)
print(arr.shape) # 形状 (2, 3)
print(arr.size) # 元素总数 (6)
print(arr.dtype) # 数据类型
print(arr.itemsize) # 每个元素字节大小
1:numpy创建数组
numpy.array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0);
| 序号 | 参数 | 描述 |
|---|---|---|
| 1 | object | 传入的准备转成numpy数组的对象,例如传入一个列表,集合等等 |
| 2 | dtype | 可选,通过这个参数可以更改元素的类型 |
| 3 | copy | 可选,当数据源是ndarray的时候是否可以复制,默认是True |
| 4 | order | 可选,使用哪种布局方式创建数组(C -> 行序列,F -> 列序列,A -> 默认) |
| 5 | subok | 可选,如果是True,使用oject内部的类型,如果是False, 使用object数组的类型 |
| 6 | ndmin | 可选,用来指定创建的数组的维度 |
object可以是数组,列表,元组,迭代对象,生成器
import numpy as np
# 创建一个数组 - 一维的 - 可以是各种可迭代对象
a = np.array([1, 2, 3])
print(a) # [1 2 3]
print(type(a)) # <class 'numpy.ndarray'>
b = np.array([1, 2, 3], dtype=np.float64)
print(b) # [1. 2. 3.]
print(type(b)) # <class 'numpy.ndarray'>
c = np.array((1, 2, 3))
print(c)
d = np.array({1: 1, 2: 2, 3: 3})
print(d)
e = np.array({1, 2, 3})
print(e)
f = np.array([i ** 2 for i in range(10)])
print(f)
🎉 如果object中的元素类型不一样的话,numpy会使用空间的最大的那个元素作为元素类型
import numpy as np
# 在这个列表中,因为字符串占的空间最大,所以是str类型
a = np.array([1, 2, 3, 4.6, "5"])
print(a) # ['1' '2' '3' '4.6' '5']
print(type(a)) # <class 'numpy.ndarray'>
# 获取每一个元素的类型
for i in a:
print(type(i)) # <class 'str'>
🎉 创建对应的二维数组的话,就是嵌套的列表和元组
import numpy as np
a = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]], dtype=np.int32)
print(a)
print(a.shape) # (2, 5) -> (row, column)
print(a.dtype) # int32 -> 每一个元素的数据类型
print(a.size) # 10 -> 元素的数量
c = np.array([[1, 2, 3], ['a', 'b', 'c']])
print(c) # 因为字符串的大小大于整数,所以数据类型为str
print(c.shape) # (2, 3) -> (row, column)
print(c.dtype) # <u11 -> unicode长度为11的str -> 每一个元素的数据类型
print(c.size) # 6
🎉 float -> int的转换会向下取整
import numpy as np
a = np.array([1, 2.5, 3, 4.5, 4.2], dtype=np.int32)
print(a) # [1 2 3 4 4] -> 可见float -> int是下取整
print(a.dtype) # int32
print(a.shape) # (5,) -> 一维数组
print(a.size) # 5 -> 元素个数
2:特殊的数组创建
| 特殊数组 | 说明 |
|---|---|
np.zero(数组的维度说明) | 全0数组 |
np.ones(数组的维度说明) | 全1数组 |
np.empty(数组的维度说明) | 未初始化数组 |
np.arange(end) | 类比于range |
np.linspace(start, end, count) | 线性间隔数组 |
np.eye(单位矩阵的大小) | 单位矩阵 - 主对角线是1, 其他全是0 |
np.random.random(数组的维度说明) | 随机数组 |
import numpy as np
a = np.zeros((3, 4)) # 全0数组
print(a) # 3行4列的全0数组 - 二维数组
print(a.dtype) # dtype=float64
print(a.shape) # (3, 4) -> 3行4列
print(a.size) # 12个元素
print(a.ndim) # 2维
b = np.ones((2, 3, 4)) # 全1数组
print(b) # 2行3列3维全1数组 - 三维数组
print(b.dtype) # dtype=float64
print(b.shape) # (2, 3, 4) -> 三维的
print(b.size) # 24个元素 (2 * 3 * 4)
print(b.ndim) # 3维
c = np.empty((2, 3)) # 未初始化数组
print(c) # 2行3列未初始化数组(0 ~ 1的随机) - 二维数组
print(c.dtype) # dtype=float64
print(c.shape) # (2, 3)
print(c.size) # 6个元素
print(c.ndim) # 2维
d = np.arange(10) # 类似range的数组 -> [i for i in range(10)]
print(d) # [0 1 2 3 4 5 6 7 8 9]
print(d.dtype) # dtype=int64
print(d.shape) # (10,)
print(d.size) # 10个元素
print(d.ndim) # 1维
e = np.linspace(0, 1, 5) # 线性间隔数组 在0~1之间线性间隔放5个数 [0., 0.25, 0.5, 0.75, 1.]
print(e) # [0. 0.25 0.5 0.75 1. ]
print(e.dtype) # dtype=float64
print(e.shape) # (5,)
print(e.size) # 5个元素
print(e.ndim) # 1维
f = np.eye(3) # 3x3单位矩阵
print(f) # [ [1, 0, 0] [0, 1, 0] [0, 0, 1] ]
print(f.dtype) # dtype=float64
print(f.shape) # (3, 3)
print(f.size) # 9个元素
print(f.ndim) # 2维
g = np.random.random((2, 2)) # 随机数组
print(g) # 2 * 2的0 ~ 1的随机数组
print(g.dtype) # dtype=float64
print(g.shape) # (2, 2)
print(g.size) # 4个元素
print(g.ndim) # 2维
三:数组的索引和切片
1:数组的基本索引
和python中的列表的索引非常相似
import numpy as np
arr = np.array([0, 1, 2, 3, 4, 5])
print(arr) # [0, 1, 2, 3, 4, 5]
print(arr[1]) # 1
print(arr[1:3]) # array([1, 2])
print(arr[::2]) # 步长2 array([0, 2, 4])
print(arr[::-1]) # 反转 array([5, 4, 3, 2, 1, 0])
print(arr[::-2]) # 反转步长2 array([5, 3, 1])
print(arr[-1]) # -1 表示最后一个 -> 5
print(arr[-2]) # -2 倒数第二个 -> 4
2:多维数组的索引
对于 n 维数组,可以使用 n 个索引值(逗号分隔)来访问元素。
下面以这个数组为例:
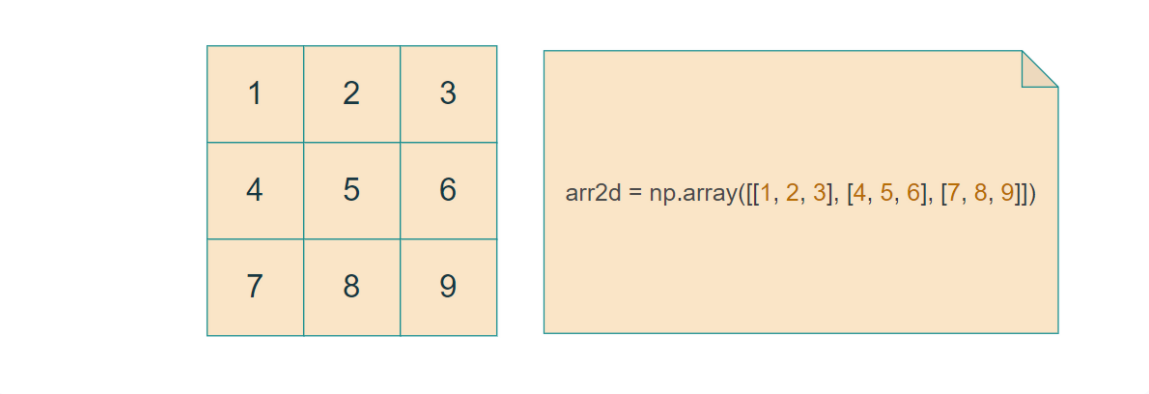
import numpy as np
arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(arr2d[0]) # 第一行 array([1, 2, 3])
print(arr2d[0, 1]) # 第一行第二列元素 (2) -> 0表示先截取第一行[1, 2, 3],1表示截取第二列2
print(arr2d[:, 1]) # 第二列 array([2, 5, 8]) -> 冒号表示截取所有行,1表示截取第二列
print(arr2d[1:3, 0:2]) # 子数组 array([[4, 5], [7, 8]]) -> 1:3表示截取第二行和第三行,0:2表示截取第一列和第二列
再举一个三维的例子
第一个参数位置的截断表示是第几个子数组
第二个参数位置的截断表示是当前子数组的第几行
第三个参数位置的截断表示当前行的第几列
import numpy as np
# 创建一个3维数组 (2x3x4)
arr = np.arange(24).reshape(2, 3, 4)
print(arr)
"""
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
"""
# 访问单个元素
print(arr[0, 1, 2]) # 输出: 6 (第0个二维数组 -> 第1行 -> 第2列)
# 访问子数组
print(arr[1]) # 获取第1个二维数组
"""
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
"""
print(arr[:, 1, :]) # 获取所有二维数组的第1行
"""
[[ 4 5 6 7]
[16 17 18 19]]
"""
# 获取所有二维数组的第0行和第1行
print(arr[:, 0:2, :])
"""
[[[ 0 1 2 3]
[ 4 5 6 7]]
[[12 13 14 15]
[16 17 18 19]]]
"""
# 使用步长
print(arr[::2, ::2, ::2]) # 每隔一个元素取一个
"""
[[[ 0 2]
[ 8 10]]]
"""
# 省略某些维度的索引
print(arr[1, ...]) # 等同于 arr[1, :, :]
"""
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
"""
3:布尔索引
布尔索引指的是使用一个与数组形状相同的布尔数组来选择元素:
当对应位置的布尔值是true的时候,表示选中此元素,否则表示非选中
import numpy as np
# 使用布尔索引的简单示例
arr = np.array([1, 2, 3, 4, 5])
mask = np.array([True, False, True, False, True])
result = arr[mask]
print(result) # [1 3 5]
# 创建布尔索引
# 方式一:直接比较操作
mask = arr > 2 # 创建一个布尔数组,值为True的元素对应于arr中大于2的元素
result = arr[mask]
print(result) # [3 4 5]
# 方式二:使用逻辑运算符 & | ~
mask = (arr > 2) & (arr < 5) # 创建一个布尔数组,值为True的元素对应于arr中大于2且小于5的元素
result = arr[mask]
print(result) # [3 4]
mask = ~(arr > 2) # 创建一个布尔数组,值为True的元素对应于arr中小于等于2的元素
result = arr[mask]
print(result) # [1 2]
# 方式三:使用布尔函数
mask = np.isin(arr, [2, 4, 6, 8, 10]) # 创建一个布尔数组,值为True的元素对应于arr中包含2或4或6或8的元素
result = arr[mask]
print(result) # [2 4]
# 可以结合多个条件
condition1 = arr > 2
condition2 = arr % 2 == 0
mask = condition1 & condition2
result = arr[mask]
print(result) # [4]
# 还可以同时指定赋值
arr[arr > 3] = 0
print(arr) # [1, 2, 3, 0, 0]
4:花式索引(难点)
花式索引(Fancy Indexing)是NumPy中一种强大的索引方式,它允许你使用整数数组来索引数组元素,提供了比基本切片更灵活的数据访问方式。
import numpy as np
# 花式索引指的是使用整数数组(而不是单个整数或切片)来索引数组
arr = np.array([1, 2, 3, 4, 5])
indices = np.array([1, 3, 4]) # 选择第2、第4和第5个元素
print(arr[indices])
# 一维数组的花式索引介绍
arr = np.arange(10, 100, 10) # array([10, 20, 30, 40, 50, 60, 70, 80, 90])
# 选择特定位置的元素
print(arr[[0, 2, 5]]) # array([10, 30, 60])
# 可以重复选择
print(arr[[1, 1, 1, 7]]) # array([20, 20, 20, 80])
# 可以使用负数索引 -1 表示最后一个元素, -2 表示倒数第二个元素...
print(arr[[-1, -3]]) # array([90, 70])
# 二维数组的花式索引介绍[ [第一维度的约束] [第二维度的约束] ]
# 1:多维数组中的单维度花式索引
arr_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 选择特定行 -> 选择第1行和第3行
print(arr_2d[[0, 2]]) # array([[1, 2, 3], [7, 8, 9]])
# 选择特定列 -> 行部分是:, 表示选择所有的行,列部分 是[1, 2],表示选择第2列和第3列
print(arr_2d[:, [1, 2]]) # array([[2, 3], [5, 6], [8, 9]])
# 2:多维数组中的多维度花式索引
# 选择特定行和列的组合
rows = [0, 1, 2] # 选择第1行,第2行,第3行
cols = [1, 0, 2] # 选择第2列,第1列,第3列
print(arr_2d[rows, cols]) # array([2, 4, 9]) - 选择(0,1), (1,0), (2,2)
# np.ix_函数可以生成一个开放网格,用于更复杂的花式索引:
print(arr_2d[np.ix_([0, 2], [1, 2])])
# 相当于 arr_2d[[0, 2]][:, [1, 2]]
# 结果为 array([[2, 3], [8, 9]])
# 花式索引的应用
# 1:数组重新排序
arr = np.array([10, 20, 30, 40, 50])
indices = [4, 0, 2, 1, 3]
print(arr[indices]) # array([50, 10, 30, 20, 40])
# 2:从多维数组中选择特定元素
# 创建一个4x4数组
arr = np.arange(16).reshape(4, 4)
# 选择四个角的元素(0, 0) (0, -1) (-1, 0) (-1, -1)
corners = arr[[0, 0, -1, -1], [0, -1, 0, -1]]
print(corners) # array([ 0, 3, 12, 15])
# 3:使用布尔数组转换为整数索引
arr = np.array([5, 10, 15, 20])
mask = np.array([True, False, False, True])
indices = np.where(mask)[0] # 转换为整数索引 array([0, 3])
print(arr[indices]) # array([5, 20])
- 花式索引通常比切片慢,因为它需要复制数据
- 对于大型数组,花式索引可能会消耗较多内存
- 在某些情况下,可以使用布尔索引替代花式索引以获得更好的性能
5:各个索引的比较
| 特性 | 切片 | 布尔索引 | 花式索引 |
|---|---|---|---|
| 返回类型 | 视图(View) | 副本(Copy) | 副本(Copy) |
| 索引方式 | 连续范围 | 条件选择 | 任意位置选择 |
| 内存效率 | 高 | 中等 | 低 |
| 速度 | 最快 | 快 | 较慢 |
| 是否可重复 | 否 | 是 | 是 |
四:数组的操作
🎉 这部分的学习要对矩阵的概念和操作有非常深刻的理解
1:对于形状的操作
可以通过np.shape查看当前的数组的形状信息
改变数组的形状 - reshape & resize
# reshape -> 改变数组形状而不改变数据
# 将12个元素的一维数组重塑为3x4的二维数组
new_arr = arr.reshape(3, 4)
print(new_arr)
"""
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
"""
# 使用-1自动计算维度大小
auto_arr = arr.reshape(2, -1) # 2行,自动计算列数(6)
print(auto_arr.shape) # 输出: (2, 6)
# resize -> 改变数组形状并可能修改数据
arr.resize(4, 3) # 直接修改原数组形状
print(arr)
"""
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
"""
# 如果新形状大于原数组,会用0填充
arr.resize(5, 3)
print(arr)
"""
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[ 0 0 0]]
"""
展平数组 - flatten(返回的副本) & ravel(返回的视图)
import numpy as np
# define a 2d array
arr_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# flatten the array
arr_2d_flattened = arr_2d.flatten()
print(arr_2d_flattened) # output: [1 2 3 4 5 6 7 8 9]
# ravel the array
# return the view of the array
# changes to the raveled array will be reflected in the original array
arr_2d_raveled = arr_2d.ravel()
print(arr_2d_raveled)
arr_2d_raveled[0] = 0
print(arr_2d) # will change the original array
转置数组 - T属性 & transpose & swapaxes
import numpy as np
# define a 2d array
arr = np.array([[1, 2, 3], [4, 5, 6]])
print(arr) # [ [1, 2, 3] [4, 5, 6] ]
print("-----------------")
print(arr.T) # [[1, 4] [2, 5] [3, 6]]
print("-----------------")
print(arr.T.T) # [[1, 2, 3] [4, 5, 6]]
# 对于2d的数组,transpose(arr_2d)和T属性一致
# 对于3d的数组,transpose可以按照指定的轴进行转置
import numpy as np
arr = np.arange(24).reshape(2, 3, 4)
print(arr) # 2个子数组,每个子数组3行4列
print(arr.shape) # (2, 3, 4)
new_arr = np.transpose(arr, (1, 0, 2)) # 将arr的第一个轴和第二个轴转置
print(new_arr) # 3个子数组,每个子数组2行4列
print(new_arr.shape) # (3, 2, 4)
arr = np.arange(24).reshape(2, 3, 4)
print(arr) # 2个子数组,每个子数组3行4列
print(arr.shape) # (2, 3, 4)
# 可以使用swapaxes()方法交换两个轴的顺序
ans = arr.swapaxes(0, 1) # 交换第0轴和第1轴
print(ans)
print(ans.shape)
增加、减少维度 - newaxis & squeeze & vstack & hstack & dstack
import numpy as np
# newaxis -> 创建一个新轴,用于在数组中增加维度。
def newaxis_test():
vec = np.array([1, 2, 3])
print(vec.shape) # 输出: (3,)
# 增加行维度(变为列向量)
col_vec = vec[:, np.newaxis]
print(col_vec.shape) # 输出: (3, 1)
print(col_vec) # [ [1] [2] [3] ]
# squeeze -> 会移除指定轴长度为1的维度。
# 如果没有指定轴,则会移除所有长度为1的维度。
def squeeze_test():
# 创建一个有冗余维度的数组
arr = np.arange(6).reshape(1, 2, 3, 1)
print(arr.shape) # 输出: (1, 2, 3, 1)
# 移除所有长度为1的维度
squeezed = arr.squeeze()
print(squeezed.shape) # 输出: (2, 3)
# 只移除特定位置的维度
squeezed_axis = arr.squeeze(axis=0)
print(squeezed_axis.shape) # 输出: (2, 3, 1)
def stack_test():
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
# 堆叠两个数组, axis=0 表示堆叠在第一维上
stacked = np.stack((arr1, arr2), axis=0)
print(stacked.shape) # 输出: (2, 3)
print(stacked) # [[1, 2, 3], [4, 5, 6]]
# 堆叠两个数组, axis=1 表示堆叠在第二维上
stacked2 = np.stack((arr1, arr2), axis=1)
print(stacked2.shape) # 输出: (3, 2)
print(stacked2) # [[1, 4], [2, 5], [3, 6]]
# hstack -> 水平堆叠
stacked1 = np.hstack((arr1, arr2))
print(stacked1.shape) # 输出: (6,)
print(stacked1) # [1, 2, 3, 4, 5, 6]
# vstack -> 垂直堆叠
stacked3 = np.vstack((arr1, arr2))
print(stacked3.shape) # 输出: (2, 3)
print(stacked3) # [[1, 2, 3], [4, 5, 6]]
# dstack -> 深度堆叠
stacked4 = np.dstack((arr1, arr2))
print(stacked4.shape) # 输出: (1, 3, 2)
print(stacked4) # [[[1, 4] [2, 5] [3,6]]]
if __name__ == '__main__':
stack_test()
2:数组重复的操作
tile & repeat
import numpy as np
def tile_test():
a = np.array([1, 2, 3])
print(np.tile(a, 2)) # 输出: [1 2 3 1 2 3]
print(np.tile(a, (2, 1))) # 沿行重复2次,列重复1次 [[1 2 3] [1 2 3]]
print(np.tile(a, (2, 2))) # 沿行重复2次,列重复2次 [[1 2 3 1 2 3] [1 2 3 1 2 3]]
def repeat_test():
a = np.array([1, 2, 3])
print(np.repeat(a, 2)) # 每个元素重复2次: [1 1 2 2 3 3]
print(np.repeat(a, [2, 1, 3])) # 指定每个元素的重复次数: [1 1 2 3 3 3]
# 对于多维数组,可以指定轴
arr_2d = np.array([[1, 2], [3, 4]])
print(np.repeat(arr_2d, 2, axis=0)) # 沿行重复[ [1 2] [1 2] [3 4] [3 4]]
print(np.repeat(arr_2d, 2, axis=1)) # 沿列重复[ [1 1 2 2] [3 3 4 4]]
if __name__ == '__main__':
tile_test()
repeat_test()
3:数组的分割操作
split & vsplit & hsplit & dsplit
import numpy as np
def split_test():
a = np.arange(9) # 0,1,2,3,4,5,6,7,8
res = np.split(a, 3) # 将数组分成3个相等的部分
print(res)
print(res[0])
print(res[1])
print(res[2])
# 可以在指定的位置进行分割
res2 = np.split(a, [4, 6])
print(res2)
print(res2[0]) # [0 1 2 3]
print(res2[1]) # [4 5]
print(res2[2]) # [6 7 8]
# vsplit -> 垂直截切, 默认是水平方向,第一个轴切割
arr = np.arange(16).reshape(4, 4)
res3 = np.vsplit(arr, 2) # 垂直切割,前两行是一个,后两行是一个
print(res3)
print(res3[0])
print(res3[1])
# hsplit -> 水平切割,第二个轴切割
res4 = np.hsplit(arr, 2) # 水平切割,前两列是一个,后两列是一个
print(res4)
print(res4[0])
print(res4[1])
# dsplit -> 垂直切割,第三个轴切割
arr_3d = np.arange(16).reshape(2, 2, 4)
print(arr_3d)
res5 = np.dsplit(arr_3d, 2) # 第一个子数组是一个,第二个子数组是一个
print(res5[0])
print(res5[1])
if __name__ == '__main__':
split_test()
五:数组通用函数
1:数学运算
import numpy as np
def base_operation():
a = np.array([1, 2, 3, 4, 5])
b = np.array([2, 4, 6, 8, 10])
print(a + b)
print(np.add(a, b)) # [3 6 9 12 15]
print(a - b)
print(np.subtract(a, b)) # [-1 -2 -3 -4 -5]
print(a * b)
print(np.multiply(a, b)) # [2 8 18 32 50]
print(a / b)
print(np.divide(a, b)) # [0.5 0.5 0.5 0.5 0.5]
print(a // b)
print(np.floor_divide(a, b)) # [0 0 0 0 0]
print(a ** 2)
print(np.power(a, 2)) # [1 4 9 16 25]
print(b % a)
print(np.mod(b, a)) # [1 0 1 0 1]
# 累计和
print(np.cumsum(a)) # [1 3 6 10 15]
# 累计积
print(np.cumprod(a)) # [1 2 6 ]
# 差分
arr = np.array([1, 2, 3, 4, 5])
print(np.diff(arr)) # [1 1 1 1]
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
print(np.diff(arr_2d)) # [[1 1] [1 1]]
2:矩阵运算
import numpy as np
def linear_algebra_test():
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
# 矩阵乘法
print(np.matmul(a, b)) # 矩阵乘法
print(a @ b) # python3.5+推荐使用 @ 运算符
print(np.dot(a, b)) # 对于2D数组的矩阵乘法,等价于matmul
# 矩阵转置
print(a.T) # [ [1 3] [2 4] ]
# 矩阵点积
print(np.vdot(a, b)) # 70 -> 1 * 5 + 2 * 7 + 3 * 9 + 4 * 11
# 逆矩阵
print(np.linalg.inv(a)) # [ [-2. 1.] [1.5 -0.5] ]
# 矩阵的行列式
print(np.linalg.det(a)) # 输出:-2.000000000004
# 对于一维数组的dot, 相当于向量点积
w = np.array([1, 2, 3, 4])
v = np.array([5, 6, 7, 8])
print(np.dot(w, v)) # 输出:70 <- 1 * 5 + 2 * 6 + 3 * 7 + 4 * 8
# 矩阵的迹(主对角线元素和)
print(np.trace(a)) # 输出:5
if __name__ == '__main__':
linear_algebra_test()
3:三角函数,指数和对数
import numpy as np
def math_test():
radio = np.array([0, np.pi / 2, np.pi])
print(np.sin(radio)) # [0.0000000e+00 1.0000000e+00 1.2246468e-16]
print(np.cos(radio)) # [ 1.000000e+00 6.123234e-17 -1.000000e+00]
print(np.tan(radio)) # [ 0.000000e+00 1.6331239e+16 -1.22464680e-16]
print(np.arcsin(np.sin(radio))) # [0.00000000e+00 1.57079633e+00 1.22464680e-16]
print(np.arccos(np.cos(radio))) # [0. 1.57079633 3.14159265]
print(np.arctan(np.tan(radio))) # [ 0.00000000e+00 1.57079633e+00 -1.22464680e-16]
x = np.array([-1, 0, 1])
print(np.arcsin(x)) # [-1.57079633 0. 1.57079633]
print(np.arccos(x)) # [3.14159265 1.57079633 0. ]
print(np.arctan(x)) # [-0.78539816 0. 0.78539816]
x = np.array([1, 2, 3])
# 指数e^x
print(np.exp(x)) # [ 2.71828183 7.3890561 20.08553692]
# 自然对数lnx
print(np.log(x)) # [0. 0.69314718 1.09861229]
# 以2为底的对数 logx
print(np.log2(x)) # [0. 1. 1.5849625]
# 以10为底的对数lgx
print(np.log10(x)) # [0. 0.30103 0.47712125]
# 其他指数 exp2 -> 2^x power(底数,幂数)
print(np.exp2(x)) # [2. 4. 8.]
print(np.power(2, x)) # 等效操作 [2 4 8]
if __name__ == "__main__":
math_test()
4:舍入和比较运算
arr = np.array([1.23, 2.56, 3.789])
# 四舍五入
print(np.round(arr)) # [1. 3. 4.]
print(np.round(arr, 1)) # 保留1位小数 [1.2 2.6 3.8]
# 向下取整
print(np.floor(arr)) # [1. 2. 3.]
# 向上取整
print(np.ceil(arr)) # [2. 3. 4.]
# 截断小数部分
print(np.trunc(arr)) # [1. 2. 3.]
# 固定小数位数
print(np.around(arr, 2)) # [1.23 2.56 3.79]
a = np.array([1, 2, 3])
b = np.array([2, 2, 2])
# 元素比较
print(a == b) # [False True False]
print(np.equal(a, b)) # 等效操作
print(a > b) # [False False True]
print(np.greater(a, b))
# 数组整体比较
print(np.array_equal(a, b)) # False
# 其他比较操作
print(a >= b) # [False True True]
print(a < b) # [ True False False]
print(a != b) # [ True False True]
5:逻辑运算
x = np.array([True, False, True])
y = np.array([False, False, True])
# 逻辑与
print(np.logical_and(x, y)) # [False False True]
# 逻辑或
print(np.logical_or(x, y)) # [ True False True]
# 逻辑非
print(np.logical_not(x)) # [False True False]
# 异或
print(np.logical_xor(x, y)) # [ True False False]
6:线性代数运算
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
# 解线性方程组
# 解 Ax = b
b = np.array([1, 2])
x = np.linalg.solve(A, b)
print(x) # [ 0. 0.5]
# 特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)
print("特征值:", eigenvalues) # [-0.37228132 5.37228132]
print("特征向量:\n", eigenvectors)
"""
[[-0.82456484 -0.41597356]
[ 0.56576746 -0.90937671]]
"""
# 奇异值分解
U, S, V = np.linalg.svd(A)
print("U:\n", U)
print("奇异值:", S)
print("V:\n", V)
7:广播
# 广播允许不同的形状的数组进行运算
# 标量与数组运算
print(a + 1) # [2 3 4]
# 不同形状数组运算
matrix = np.array([[1, 2, 3], [4, 5, 6]])
row = np.array([10, 20, 30])
print(matrix + row)
"""
[[11 22 33]
[14 25 36]]
"""
column = np.array([[10], [20]])
print(matrix + column)
"""
[[11 12 13]
[24 25 26]]
"""
8:实用数学函数和应用
# 绝对值
x = np.array([-1, 0, 1])
print(np.abs(x)) # [1 0 1]
# 符号函数
print(np.sign(x)) # [-1 0 1]
# 平方根
print(np.sqrt(np.abs(x))) # [1. 0. 1.]
# 阶乘
print(np.math.factorial(5)) # 120 (注意:只适用于标量)
# 叉积(仅限3D向量)
a = np.array([1, 0, 0])
b = np.array([0, 1, 0])
print(np.cross(a, b)) # [0 0 1]
# Z-score标准化
data = np.random.randn(100, 5) # 100样本,5特征
normalized = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
# Min-Max归一化
scaled = (data - np.min(data)) / (np.max(data) - np.min(data))
# 计算多项式 p(x) = x³ + 2x² + 3x + 4
coefficients = [1, 2, 3, 4]
x = 2
print(np.polyval(coefficients, x)) # 26 (8 + 8 + 6 + 4)
# 多项式拟合
x = np.array([0, 1, 2, 3])
y = np.array([1, 3, 7, 13])
coefficients = np.polyfit(x, y, 2) # 二次多项式拟合
# 欧氏距离
point1 = np.array([1, 2, 3])
point2 = np.array([4, 5, 6])
distance = np.linalg.norm(point1 - point2)
print(distance) # 5.196152422706632
# 点积计算角度
a = np.array([1, 0])
b = np.array([0, 1])
cos_theta = np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b))
angle = np.arccos(cos_theta) # 弧度
print(np.degrees(angle)) # 90.0度
六:高级特性
1:结构化数组
结构化数组允许在单个数组中存储不同类型的数据,类似于数据库表格或 Pandas DataFrame。
import numpy as np
def struct_array_test():
# 创建结构数组
# 定义name是字符串(占据10个字符的unicode),age是int(占据4个字符),weight是float(占据4个字符)
# 可以类比一下类
my_type = [('name', 'U10'), ('age', 'i4'), ('weight', 'f4')]
data = np.array([
('john', 50, 48.5),
('mary', 45, 70.5),
('jane', 35, 50.5)
], dtype=my_type) # 声明使用自己定义的结构
print(data['name']) # ['john' 'mary' 'jane']
print(data['age']) # [50 45 35]
print(data[0]) # ('john', 50, 48.5)
# 还可以进行一些高级操作
# 筛选 - 将结构数组中age大于40的行打印出来
print(data[data['age'] > 40]) # [('john', 50, 48.5) ('mary', 45, 70.5)]
# 按照指定的字段进行排序
print(np.sort(data, order='weight')) # 按weight排序 [('john', 50, 48.5) ('jane', 35, 50.5) ('mary', 45, 70.5)]
if __name__ == '__main__':
struct_array_test()
2:内存映射
处理超大数组时,可以使用内存映射将磁盘上的二进制文件直接映射到内存。
# 创建内存映射
large_array = np.memmap('large_array.npy', dtype='float32', mode='w+', shape=(10000, 10000))
# 常规操作
large_array[0] = np.random.rand(10000)
large_array[:, 0] = 1.0
# 显式保存更改
del large_array # 关闭内存映射并保存更改
3:通用函数ufunc
import numpy as np
# 定义一个普通函数my_func,接受两个参数x和y,并返回x的平方加上y的平方
def my_func(x, y):
return x ** 2 + y ** 2
# 使用np.frompyfunc将my_func转换为一个numpy的通用函数(ufunc)
# 第一个参数是要进行转换的函数my_func
# 第二个参数2是它接受2个输入参数
# 第三个参数1是返回1个输出
my_ufunc = np.frompyfunc(my_func, 2, 1)
# 调用my_ufunc函数,第一个参数是0到2的数组([0, 1, 2]),第二个参数是[2, 3, 4]
# 计算结果并赋值给result
result = my_ufunc(np.arange(3), np.array([2, 3, 4]))
# 打印result数组的内容,预期输出:[4 10 20]
print(result) # [4 10 20]
arr = np.array([1, 2, 3, 4])
# 累积运算
print(np.add.accumulate(arr)) # [ 1 3 6 10]
# 归约运算
print(np.multiply.reduce(arr)) # 24 (1*2*3*4)
4:高级广播技巧
# 使用 np.newaxis 控制广播
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
# 外积计算
print(a[:, np.newaxis] * b)
"""
[[ 4 5 6]
[ 8 10 12]
[12 15 18]]
"""
# np.broadcast_to 显式广播
arr = np.array([1, 2, 3])
broadcasted = np.broadcast_to(arr, (3, 3))
print(broadcasted)
"""
[[1 2 3]
[1 2 3]
[1 2 3]]
"""
5:视图与副本的高级控制
# np.may_share_memory 检查内存共享
a = np.arange(10)
b = a[::2]
print(np.may_share_memory(a, b)) # True
# np.copy 强行创建副本,视图会影响源数组,副本不会
view = a[:5] # 切片生成的是视图
copy = np.copy(a[:5])
view[0] = 100 # 会影响a
copy[1] = 200 # 不会影响a
6:高级线性代数
A = np.random.rand(3, 3)
# LU分解
P, L, U = scipy.linalg.lu(A) # 需要SciPy
# QR分解
Q, R = np.linalg.qr(A)
# Cholesky分解
B = A @ A.T # 创建对称正定矩阵
L = np.linalg.cholesky(B)
# 计算伪逆
A_pinv = np.linalg.pinv(A)
# 最小二乘解
X = np.array([[1, 1], [1, 2], [1, 3]])
y = np.array([1, 2, 2])
beta = np.linalg.lstsq(X, y, rcond=None)[0]
7:高级随机数的生成
rng = np.random.RandomState(42) # 固定随机种子
print(rng.rand(3))
# 多种分布
print(rng.normal(0, 1, size=5)) # 正态分布
print(rng.poisson(5, size=3)) # 泊松分布
arr = np.arange(10)
# 随机排列
rng.shuffle(arr) # 原地打乱
print(rng.permutation(arr)) # 返回新数组
# 随机选择
print(rng.choice(arr, size=3, replace=False)) # 无放回抽样
8:高级数组操作
A = np.random.rand(3, 4)
B = np.random.rand(4, 5)
# 矩阵乘法
print(np.einsum('ij,jk->ik', A, B))
# 迹运算
print(np.einsum('ii', A)) if A.shape[0] == A.shape[1] else None
# 向量点积
v = np.array([1, 2, 3])
print(np.einsum('i,i', v, v)) # 14
arr = np.array([[1, 2], [3, 4]])
# 对称填充
print(np.pad(arr, ((1, 1), (1, 1)), mode='constant', constant_values=0))
"""
[[0 0 0 0]
[0 1 2 0]
[0 3 4 0]
[0 0 0 0]]
"""
9:实际应用示例
# ------------- 图像的卷积优化 ----------------
from scipy.signal import convolve2d
# 使用FFT加速的大卷积
image = np.random.rand(512, 512)
kernel = np.random.rand(32, 32)
result = convolve2d(image, kernel, mode='same', boundary='symm')
# ------------- 向量化的蒙特卡洛积分 ------------
n_samples = 1_000_000
x = np.random.rand(n_samples)
y = np.random.rand(n_samples)
inside = (x**2 + y**2) <= 1
pi_estimate = 4 * np.mean(inside)
# ------------ 时间序列分析 -----------------
# 使用滑动窗口进行高效计算
def rolling_window(a, window):
shape = a.shape[:-1] + (a.shape[-1] - window + 1, window)
strides = a.strides + (a.strides[-1],)
return np.lib.stride_tricks.as_strided(a, shape=shape, strides=strides)
ts = np.random.randn(1000)
windowed = rolling_window(ts, 30)
moving_avg = windowed.mean(axis=-1)





















 661
661

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








