题目链接
https://leetcode-cn.com/problems/as-far-from-land-as-possible/
描述
你现在手里有一份大小为 N x N 的 网格 grid,上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,
请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是
|x0 - x1| + |y0 - y1| 。
如果网格上只有陆地或者海洋,请返回 -1。
提示:
1 <= grid.length == grid[0].length <= 100
grid[i][j] 不是 0 就是 1
示例
示例 1:
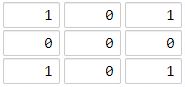
输入:[[1,0,1],[0,0,0],[1,0,1]]
输出:2
解释:
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大,最大距离为 2。
示例 2:
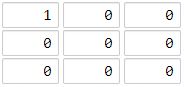
输入:[[1,0,0],[0,0,0],[0,0,0]]
输出:4
解释:
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大,最大距离为 4。
初始代码模板
class Solution {
public int maxDistance(int[][] grid) {
}
}
代码
多源BFS,这次的官方题解蛮不错的:
https://leetcode-cn.com/problems/as-far-from-land-as-possible/solution/di-tu-fen-xi-by-leetcode-solution/
class Solution {
public int maxDistance(int[][] grid) {
final int INF = 10_0000;
int[] dx = {1, -1, 0, 0};
int[] dy = {0, 0, 1, -1};
int n = grid.length;
int[][] arr = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
arr[i][j] = INF;
}
}
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
arr[i][j] = 0;
queue.offer(new int[]{i, j});
}
}
}
while (!queue.isEmpty()) {
for (int size = queue.size(); size > 0; size--) {
int[] cur = queue.poll();
for (int i = 0; i < dx.length; i++) {
int newX = cur[0] + dx[i];
int newY = cur[1] + dy[i];
if (newX < 0 || newX >= n || newY < 0 || newY >= n) {
continue;
}
if (arr[newX][newY] == INF) {
arr[newX][newY] = arr[cur[0]][cur[1]] + 1;
queue.offer(new int[]{newX, newY});
}
}
}
}
int res = -1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 0) {
res = Math.max(res, arr[i][j]);
}
}
}
return res == INF ? -1 : res;
}
}





















 430
430

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








