数据压缩第十一次作业

完全重建QMF滤波器

主要学习《完全重建QMF滤波器组的设计》文献

1.两通道正交镜像滤波器组理论

在分析滤波器组一侧，输入信号（设为宽带信号）被分成K个子频带信号（窄带信号），通过抽取可降低采样率；在综合滤波器一侧，通过零值内插和带通滤波可以重建原来的信号。



对于一个给定的信号，在经过分析滤波器、抽取等等一系列操作后得到回复和重建，但是重建后的信号与原信号存在着误差，主要包括混叠失真、幅度失真、相位失真以及量化失真。

在设计量化器时，就就需要综合考虑如何减小和消除上述的各类误差。消除混叠失真一种简单形式采取：

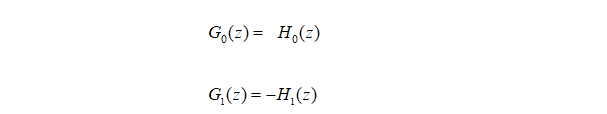
当两通道无混叠滤波器组的分解滤波器满足：

时，该滤波器组为正交镜像滤波器组。且滤波器的幅度特性满足

2.完全重建QMFB遇到的问题和解决办法
问题：在完全重建QMFB过程中，希望设计的滤波器通带尽量平、过渡带尽量窄，且阻带尽可能快速衰减。但是由假设得到的H0(z)和H1(z)和不能满足这些要求，因此它们没有实用的意义。
解决：（1）用FIR QMF滤波器组，去除相位失真的前提下，尽可能的减小幅度失真，近似实现完全重建；
（2）用IIR QMF滤波器组，去除幅度失真，不考虑相位失真，近似实现完全重建；
（3）修正QMF滤波器H1(z)=H0(-z)的关系，去考虑更合理的形式，从而实现完全重建。

3.完全重建QMFB的设计
完全重建QMFB需要找到合适的N和w的值，使得重建效果最好。为此，首先选定w，对应不同的输入信号x(n)，改变N的大小求出均方误差mse，通过比较得到最优的N值；其次，固定N，对应不同的输入信号x(n)，改变w的大小求出均方误差mse，通过比较得到最优的w值。至此，找到了使得完全重建QMFB效果最好的参数N和w。
N=41;w=0.43

任务一： 根据文献最后的代码在matlab上运行得到：

matlab代码实现：

clear;
close all;

N=41;
w=0.43;
[h0,h1,g0,g1]=firpr2chfb(N,w);
[H1z,w]=freqz(h0,1,512);
H1_abs=abs(H1z);H1_db=20*log10(H1_abs);
[H2z,w]=freqz(h1,1,512);
H2_abs=abs(H2z);H2_db=20*log10(H2_abs);
%%%%%%%%%%滤波器h0和h1的幅度响应%%%%%%%%%%
figure(1); 
plot(w/pi,H1_db,'-',w/pi,H2_db,'--'); 
axis([0,1,-100,10]); 
grid 
xlabel('\omega/\pi');ylabel('幅度,dB'); 
sum1=H1_abs.*H1_abs+H2_abs.*H2_abs; 
d=10