leetcode单调栈

目录

1. 柱状图中最大的矩形
2. 最小栈
3. 下一个更大元素 I
4. 下一个更大元素 II
5. 每日温度
6. 子数组的最小值之和
7. 移掉 K 位数字

定义：单调栈是一种特殊的栈，在这个栈内只储存递增或递减的数组。
例题：

84.柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

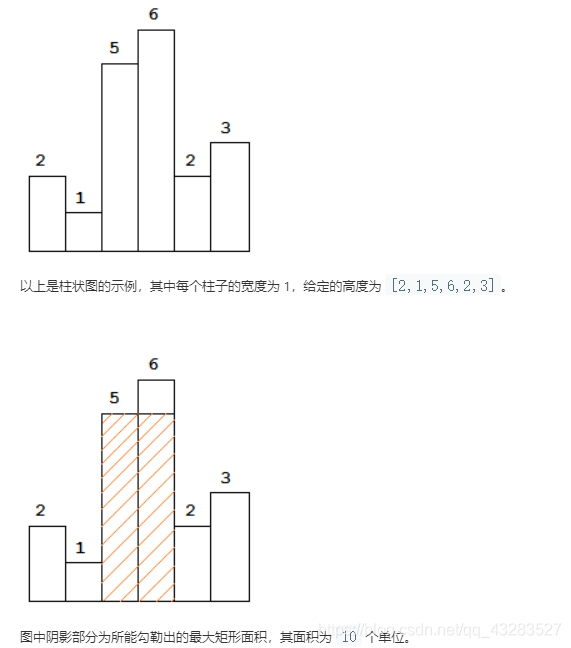
示例：

输入: [2,1,5,6,2,3]
输出: 10

解题思路：（利用单调栈）

首先在数组最后加入0，这是为了方便处理完所有高度数据，假设储存高度坐标的栈为stack，当前处理的高度坐标为i：

1. 如果当前stack为空，或者height[i]>=栈顶对应坐标的高度，则进站，i+=1
2. 当height[i] <=栈顶元素，说明可以处理栈内的坐标形成的局部递增高度。求解当前栈内形成的最大面积值。top=弹出栈顶坐标，top’ =此时栈顶新坐标。对应计算面积宽度k = i-1-top’。(若出站后stack为空，则对应宽度k=i)，面积s=heights[top] *k。再次返回2检查比较。
3. 遍历完所有i，返回面积最大值。
   代码如下:

def largestRectangleArea(heights):
	i=0
	max_area=0
	stack=[]
	heights.append(0)
	while i< len(heights):
		if len(stack)==0 or heights[stack[-1]]<=heights[i]:
			stack.append(i)
			i+=1
		else:
			top=stack.pop()
			if len(stack)==0:
				max_area=max(max_area,i*heights[top])
			else:
				max_area=max(max_area,(i-stack[-1]-1)*heihts[top])
	return max_area	

155. 最小栈
设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

辅助栈：在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时，如果栈顶元素是 a，我们就可以直接返回存储的最小值 m。

class MinStack:
    def __init__(self):
        self.stack = []
        self.min_stack = [math.inf]

    def push(self, x: int) -> None:
        self.stack.append(x)
        self.min_stack.append(min(x, self.min_stack[-1]))

    def pop(self) -> None:
        self.stack.pop()
        self.min_stack.pop()

    def top(self) -> int:
        return self.stack[-1]

    def getMin(self) -> int:
        return self.min_stack[-1]

496. 下一个更大元素 I

给定两个没有重复元素的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出-1。

解题思路：这道题本质上就是对第二个数组进行操作，找出其中所有元素对应的数字，(第一个比它大的元素或者-1)，这一步用字典储存，用栈结构实现。栈内元素储存的是递减组数。

class Solution(object):
    def nextGreaterElement(self, nums1, nums2):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :rtype: List[int]
        """
        dict={}
        stack=[]
        res=[]
        for i in nums2:
            while stack and stack[-1]<i:
                dict[stack[-1]]=i
                stack.pop()
            stack.append(i)  #栈内储存的是单调递减数组
        for i in nums1:
            res.append(dict.get(i,-1))
        return ls_ans 

503. 下一个更大元素 II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例1：

输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

解题思路：

通过单调栈来解决，但此时输入的是一个数组而且包含重复元素。对于循环数组，通常的处理手段是通过余数，然后将数组的长度扩大两倍即可。关键问题，在于如果找不到下一个更大的元素?可不需要弹出栈顶元素。此时的栈是一非严格单调的栈。

class Solution:
    def nextGreaterElements(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        stack, nums_len = list(), len(nums)
        res = [-1] * nums_len
        for i in range(nums_len*2):
            while stack and nums[stack[-1]] < nums[i%nums_len]:
                res[stack.pop()] = nums[i%nums_len]   
            stack.append(i%nums_len)
            
        return res

739. 每日温度

根据每日 气温 列表，请重新生成一个列表，对应位置的输入是你需要再等待多久温度才会升高的天数。如果之后都不会升高，请输入 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

代码如下：

class Solution(object):
    def dailyTemperatures(self, T):
        """
        :type T: List[int]
        :rtype: List[int]
        """
        res=[0]*len(T)
        stack=[]
        for i in range(len(T)):
            while stack and T[stack[-1]]<T[i]:
                index=stack.pop()
                res[index]=i-index
            stack.append(i)   
        return res

907. 子数组的最小值之和

给定一个整数数组 A，找到 min(B) 的总和，其中 B 的范围为 A 的每个（连续）子数组。

由于答案可能很大，因此返回答案模 10^9 + 7。

示例：

输入：[3,1,2,4]
输出：17
解释：
子数组为 [3]，[1]，[2]，[4]，[3,1]，[1,2]，[2,4]，[3,1,2]，[1,2,4]，[3,1,2,4]。 
最小值为 3，1，2，4，1，1，2，1，1，1，和为 17。

解题思路：

使用递增栈：当我们找到当前元素下一个更小值的同时，实际上也可以知道前一个更小的元素。

代码如下：

class Solution(object):
    def sumSubarrayMins(self, A):
        """
        :type A: List[int]
        :rtype: int
        """
        res = 0
        stack = []
        A = [0] + A + [0]
        for i in range(len(A)):
            while stack and A[stack[-1]] > A[i]:
                now_index= stack.pop()
                res += A[now_index] * (i - now_index) * (now_index - stack[-1])
            stack.append(i)
        return res % (10**9 + 7)

402. 移掉 K 位数字
贪心 + 单调栈

class Solution:
    def removeKdigits(self, num: str, k: int) -> str:
        numStack = []
        
        # 构建单调递增的数字串
        for digit in num:
            while k and numStack and numStack[-1] > digit:
                numStack.pop()
                k -= 1
        
            numStack.append(digit)
        
        # 如果 K > 0，删除末尾的 K 个字符
        finalStack = numStack[:-k] if k else numStack
        
        # 抹去前导零
        return "".join(finalStack).lstrip('0') or "0"