Luogu P2752【usaco4.3.3】街道赛跑-Street Race（图论连通性）

来源： JZOJ #310,Luogu P2752

题目描述

下图表示一次街道赛跑的跑道。可以看出有一些路口（用 0 到 N 的整数标号），和连接这些路口的箭头。路口 0 是跑道的起点，路口 N是跑道的终点。箭头表示单行道。运动员们可以顺着街道从一个路口移动到另一个路口（只能按照箭头所指的方向）。当运动员处于路口位置时，他可以选择任意一条由这个路口引出的街道。

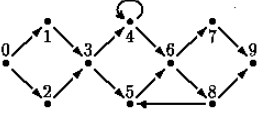
上图：有 10 个路口的街道 一个良好的跑道具有如下几个特点：
每一个路口都可以由起点到达。 从任意一个路口都可以到达终点。 终点不通往任何路口。 运动员不必经过所有的路口来完成比赛。有些路口却是选择任意一条路线都必须到达的（称为“不可避免”的）。在上面的例子中，这些路口是 0，3，6，9。对于给出的良好的跑道，你的程序要确定“不可避免”的路口的集合，不包括起点和终点。

假设比赛要分两天进行。为了达到这个目的，原来的跑道必须分为两个跑道，每天使用一个跑道。第一天，起点为路口 0，终点为一个“中间路口”；第二天，起点是那个中间路口，而终点为路口 N。对于给出的良好的跑道，你的程序要确定“中间路口”的集合。如果良好的跑道 C 可以被路口 S 分成两部分，这两部分都是良好的，并且 S 不同于起点也不同于终点，同时被分割的两个部分满足下列条件：（1）它们之间没有共同的街道（2）S 为它们唯一的公共点，并且 S 作为其中一个的终点和另外一个的起点。那么我们称 S 为“中间路口 ”。在例子中只有路口 3 是中间路口（允许中间路口可以到达本身）.

解题思路

• 这道题要分成两个问来做：
• 第一问很容易想到，题目要求我们找到不可避免的路口，我们可以枚举每个点，把这个点去掉（$f[i]$ 设为1），然后从起点 $dfs$，如果能到达终点就说明当前这个点不是必经点，反之保存在一个数组 $ans1$ 中；
• 第二问就需要思维的碰撞了，首先我们得明白中间路口必然在第一问中求出的必经点中，所以我们只要在ans1中枚举即可；$Mr.Liu$ 讲的方法是把一个必经点左边赋为真，右边赋为假，然后如果左右两个子集中任意两点有边相连，那么当前这个点一定不是中间路口；
• 这个思路可以用一种方法来实现，因为是有向图，所以可每次从一个必经点开始 $dfs$，最后判断如果当前必经点左边的子集有被访问过，说明必经点右边的子集中有点与左子集相连，形成回路，$Ofcours$