win10+Python3.7.3+OpenCV3.4.1入门学习（二十二章 K均值聚类）———— 22.1 K均值聚类理论基础

Python版本是Python3.7.3，OpenCV版本OpenCV3.4.1，开发环境为PyCharm

第22章 K均值聚类

当我们要预测的是一个离散值时，做的工作就是“分类”。例如，要预测一个孩子能否成为优秀的运动员，其实就是要将他分到“好苗子”（能成为优秀的运动员）或“普通孩子”（不能成为优秀运动员）的类别。当我们要预测的是一个连续值时，做的工作就是“回归”。例如，预测一个孩子将来成为运动员的指数，计算得到的是0.99或者0.36之类的数值。
机器学习模型还可以将训练集中的数据划分为若干个组，每个组被称为一个“簇（cluster）”。这些自动形成的簇，可能对应着不同的潜在概念，例如“篮球苗子”、“长跑苗子”。这种学习方式被称为“聚类（clusting）”，它的重要特点是在学习过程中不需要用标签对训练样本进行标注。也就是说，学习过程能够根据现有训练集自动完成分类（聚类）。
根据训练数据是否有标签，我们可以将学习划分为监督学习和无监督学习。前面介绍的K近邻、支持向量机都是监督学习，提供有标签的数据给算法学习，然后对数据分类。而聚类是无监督学习，事先并不知道分类标签是什么，直接对数据分类。
举一个简单的例子，有100粒豆子，如果已知其中40粒为绿豆，40粒为大豆，根据上述标签，将剩下的20粒豆子划分为绿豆和大豆则是监督学习。针对上述问题可以使用K近邻算法，计算当前待分类豆子的大小，并找出距离其最近的5粒豆子的大小，判断这5粒豆子中哪种豆子最多，将当前豆子判定为数量最多的那一类豆子类别。
同样，有100粒豆子，我们仅仅知道这些豆子里有两个不同的品种，但并不知道到底是什么品种。此时，可以根据豆子的大小、颜色属性，或者根据大小和颜色的组合属性，将其划分为两个类型。在此过程中，我们没有使用已知标签，也同样完成了分类，此时的分类是一种无监督学习。
聚类是一种无监督学习，它能够将具有相似属性的对象划分到同一个集合（簇）中。聚类方法能够应用于所有对象，簇内的对象越相似，聚类算法的效果越好。

22.1 理论基础

本节首先用一个实例来介绍K均值聚类的基本原理，在此基础上介绍K均值聚类的基本步骤，最后介绍一个二维空间下的K均值聚类示例。

22.1.1 分豆子

假设有6粒豆子混在一起，我们可以在不知道这些豆子类别的情况下，将它们按照直径大小划分为两类。
经过测量，以mm（毫米）为单位，这些豆子的直径大小分别为1、2、3、10、20、30。下面将它们标记为A、B、C、D、E、F，并进行分类操作。
第1步：随机选取两粒参考豆子。例如，随机将直径为1mm的豆子A和直径为2 mm的豆子B作为分类参考豆子。
第2步：计算每粒豆子的直径距离豆子A和豆子B的距离。距离哪个豆子更近，就将新豆子划分在哪个豆子所在的组。使用直径作为距离计算依据时，计算结果如下表所示。
在这里插入图片描述

在本步骤结束时，6粒豆子被划分为以下两组。
● 第1组：只有豆子A。
● 第2组：豆子B、C、D、E、F，共5粒豆子。
第3步：分别计算第1组豆子和第2组豆子的直径平均值。然后，将各个豆子按照与直径平均值的距离大小分组。
● 计算第1组豆子的平均值AV1=1mm。
● 计算第2组豆子的平均值AV2=(2+3+10+20+30)/5=13mm。
得到上述平均值以后，对所有的豆子再次分组：
● 将平均值AV1所在的组，标记为AV1组。
● 将平均值AV2所在的组，标记为AV2组。
计算各粒豆子距离平均值AV1和AV2的距离，并确定分组，如下表所示。

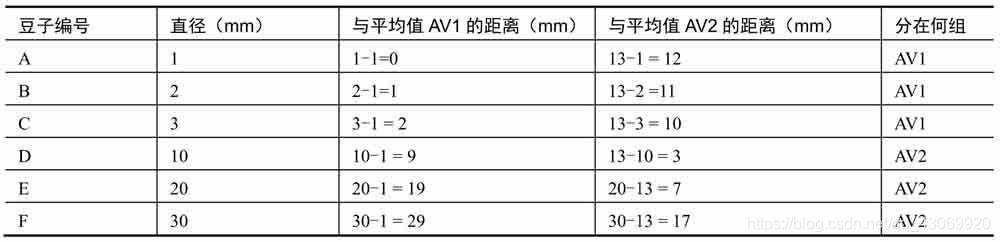
在这里插入图片描述

距离平均值AV1更近的豆子，就被划分为AV1组；距离平均值AV2更近的豆子，就被划分为AV2组。现在，6粒豆子的分组情况为：
● AV1组：豆子A、豆子B、豆子C。
● AV2组：豆子D、豆子E、豆子F。
第4步：重复第3步，直到分组稳定不再发生变化，即可认为分组完成。
在本例中，重新计算AV1组的平均值AV41、AV2组的平均值AV42，依次计算每个豆子与平均值AV41和AV42的距离，并根据该距离重新划分分组。按照与第3步相同的方法，重新计算平均值并分组后，6粒豆子的分组情况为：
● AV41组：豆子A、豆子B、豆子C。
● AV42组：豆子D、豆子E、豆子F。
与上一次的分组相比，并未发生变化，我们就认为分组完成了。我们将直径较小的那一组称为“小豆子”，直径较大的那一组称为“大豆子”。
当然，本例是比较极端的例子，数据很快就实现了收敛，在实际处理中可能需要进行多轮的迭代才能实现数据的收敛，分类不再发生变化。

22.1.2 K均值聚类的基本步骤

K均值聚类是一种将输入数据划分为k个簇的简单的聚类算法，该算法不断提取当前分类的中心点（也称为质心或重心），并最终在分类稳定时完成聚类。从本质上说，K均值聚类是一种迭代算法。
K均值聚类算法的基本步骤如下：
1．随机选取k个点作为分类的中心点。
2．将每个数据点放到距离它最近的中心点所在的类中。
3．重新计算各个分类的数据点的平均值，将该平均值作为新的分类中心点。
4．重复步骤2和步骤3，直到分类稳定。
在第1步中，可以是随机选取k个点作为分类的中心点，也可以是随机生成k个并不存在于原始数据中的数据点作为分类中心点。
在第3步中，提到的“距离最近”，说明要进行某种形式的距离计算。在具体实现时，可以根据需要采用不同形式的距离度量方法。当然，不同的计算方法会对算法的性能产生影响。