PCA与SVD的联系与区别是什么？

原理分析

PCA（主成分分析）和SVD（奇异值分解）是数据降维和特征提取的核心工具
假设数据矩阵 $X$（已中心化）：

• PCA步骤：先计算协方差矩阵 $C=\frac{1}{n-1}{X}^{T}X$，其次计算$C$的特征向量: $C$是一个对称矩阵可以被对角化，即$C=VL{V}^T$，其中$V$是特征向量，$L$是对角矩阵，其对角中间数值为 λ1，λ2，λ3，… ，则$XV$就是降维后的向量，降维的程度取前多少个特征向量。
• SVD步骤：直接分解 $X=U\Sigma V^T$，其中$U$为左奇异向量(正交)， $S$为对角矩阵中间数值为$s_1,s_2,s_3,...$，$V$为右奇异向量(正交)。
  结合SVD与PCA的步骤，有:
  $C=VS{U}^{T}US{V}^T/(n-1)=V\frac{S^2}{n-1}{V}^T$
  对比PCA的对角化的结果：有${\lambda }_i={s^2}_i/(n-1)$，且有$XV=US{V}^{T}V=US$。

区别对比

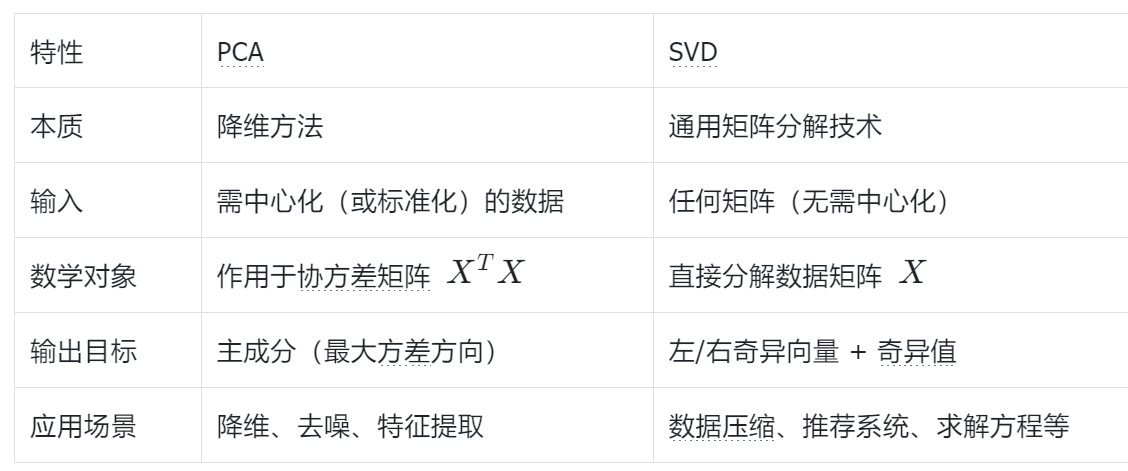
总结

1. PCA的核心数学实现可视为SVD的协方差场景特例，即当对中心化数据矩阵进行奇异值分解时，其左奇异向量直接对应主成分方向（特征空间基轴），而奇异值的平方恰为协方差矩阵的特征值（表征各维度方差能量）。这种等价性使SVD成为求解PCA的数值稳定捷径，无需显式计算协方差矩阵（避免病态条件问题），直接通过数据矩阵分解一步获得主成分与能量分布。【SVD直接分解，PCA对协方差矩阵操作后分解】
2. 奇异值和特征向量存在关系，有${\lambda }_i={s^2}_i/(n-1)$
3. SVD可以获取另一个方向上的主成分，而PCA只能获得单个方向上的主成分，PCA只与SVD的右奇异向量的压缩效果相同【SVD更加通用】
4. 通过SVD可以得到PCA相同的结果，但是SVD通常比直接使用PCA更稳定。因为在PCA求协方差时很可能会丢失一些精度。