文章目录
K M P KMP KMP:
先贴一个代码:
#include<cstdio>
#include<cstring>
using namespace std;
char a[10000009],b[100010];int la,lb,p[100010];
int main()
{
scanf("%s%s",a+1,b+1);la=strlen(a+1);lb=strlen(b+1);
for(int i=2,j=0;i<=lb;i++)
{
while(j&&b[i]!=b[j+1])j=p[j];
if(b[i]==b[j+1])p[i]=++j;
}
for(int i=1,j=0;i<=la;i++)
{
while(j&&a[i]!=b[j+1])j=p[j];
if(a[i]==b[j+1])
{
if(++j==lb){printf("%d %d\n",i-j+1,i);return 0;}
}
}
puts("NO");
return 0;
}
正确性证明:
for(int i=2,j=0;i<=lb;i++)
{
while(j&&b[i]!=b[j+1])j=p[j];
if(b[i]==b[j+1])p[i]=++j;
}
第1个
f
o
r
for
for循环是对子串的预处理,
p
[
i
]
p[i]
p[i]表示子串的前
i
i
i项前缀与后缀的最大匹配长度.
我们从2开始,是因为我们要保证前缀和后缀的最大匹配长度不为整个区间长度.
对于第1个 f o r for for我们先假设 p [ 1 p[1 p[1~~ i − 1 ] i-1] i−1]是正确的,只要我们能保证 p [ i ] p[i] p[i]的求法无误,就可以保证 p p p数组的正确性.
j
j
j为
i
i
i前面的匹配长度.那么那个
w
h
i
l
e
while
while为什么是正确的呢.
因为
b
[
i
]
!
=
b
[
j
+
1
]
b[i]!=b[j+1]
b[i]!=b[j+1],所以前
j
j
j项加上第
i
i
i项不能不能与前缀匹配,那么
j
j
j就必须变小.
因为要保证
j
j
j的变化量最小,并且变化后的
i
的前
j
项
i的前j项
i的前j项能与前缀匹配.
那么
j
j
j就应该变为前缀与后缀的最长匹配长度,即
j
=
p
[
j
]
j=p[j]
j=p[j].
那个
i
f
if
if判断显然是对的,不就不讲了.
我们证明了第1重 f o r for for循环是对的,那么第2重 f o r for for循环是类似的,我就不证明了.
一个小栗子:

a
[
i
]
!
=
b
[
j
+
1
]
a[i]!=b[j+1]
a[i]!=b[j+1]应缩小
j
j
j的大小,使得缩小后
i
的前
j
项
i的前j项
i的前j项仍能与子串前缀匹配,那么
j
j
j就应该变为后缀与前缀的最长匹配长度(即
p
[
j
]
p[j]
p[j])啦.
复杂度证明:
复杂度
O
(
l
a
+
l
b
)
O(la+lb)
O(la+lb),为什么呢——其实每重循环都是线性的。
那我就只讲第1重循环吧.
对于
w
h
i
l
e
,
j
while,j
while,j每次至少减小1.
而
j
j
j每次只增加1.
所以这个循环的复杂度就是
O
(
l
b
)
O(lb)
O(lb)的.
另一个循环的复杂度证明类似.
e x K M P exKMP exKMP:
传送门
exKMP可以线性求解最长公共前缀长度.
那么它是怎么实现的呢?——一句话:高度继承前面的判断.
思路:
我们需要预处理出子串以每一个位置开头的前缀与子串前缀的最长公共前缀长度.
设子串为
b
b
b, 长度为
l
b
lb
lb,
p
[
i
]
p[i]
p[i]表示
b
[
i
∼
l
b
]
与
b
[
1
∼
l
b
]
b [i \sim lb] 与 b[1 \sim lb ]
b[i∼lb]与b[1∼lb]的最长公共前缀长度.
设
e
d
=
max
(
i
+
p
[
i
]
−
1
)
,
k
为形成
e
d
的
i
(
k
+
p
[
k
]
−
1
为
ed=\max(i+p[i]-1),k为形成ed的i ( k +p[k]-1为
ed=max(i+p[i]−1),k为形成ed的i(k+p[k]−1为当前 最大)。
我们需要在线性时间内求出
p
p
p。
而对于
p
[
i
]
p[i]
p[i]的求法,我们需要分类讨论。

注意:上面的图画错了:
k
−
i
+
1
应为
i
−
k
+
1
k-i+1应为i-k+1
k−i+1应为i−k+1
由于
p
p
p的定义,我们可以知道
b
[
k
∼
e
d
]
=
b
[
1
∼
p
[
k
]
]
b[k \sim ed] =b[1 \sim p[k] ]
b[k∼ed]=b[1∼p[k]](红线),那么可以得到
b
[
i
∼
e
d
]
=
b
[
i
−
k
+
1
∼
p
[
k
]
]
b[i \sim ed]=b[i-k+1 \sim p[k]]
b[i∼ed]=b[i−k+1∼p[k]].
设
L
=
p
[
i
−
k
+
1
]
,
R
=
e
d
−
i
+
1
=
k
+
p
[
k
]
−
1
−
i
+
1
=
k
+
p
[
k
]
−
i
L=p[i-k+1],R=ed-i+1=k+p[k]-1-i+1=k+p[k]-i
L=p[i−k+1],R=ed−i+1=k+p[k]−1−i+1=k+p[k]−i.
若
L
<
R
L<R
L<R,如上图,蓝线表示
L
L
L.则根据
p
p
p的定义有:
b
[
L
+
1
]
≠
b
[
i
+
L
]
b[L+1]\ne b[i+L]
b[L+1]=b[i+L],
p
[
i
]
=
L
p[i]=L
p[i]=L
否则,如下图。

注意:上面的图画错了:
k
−
i
+
1
应为
i
−
k
+
1
k-i+1应为i-k+1
k−i+1应为i−k+1
我们直接暴力拓展,再更新
k
k
k即可。
需要注意的是点可能已经超过了
e
d
ed
ed.
我们现在已经完成了 b b b串的处理。关于 a 与 b a与b a与b的公共前缀,其实做法类似,这里就不赘述了。
代码:
int n, m, p[N], ex[N];
char a[N], b[N];
void solve() {
scanf("%s %s", a + 1, b + 1); n = strlen(a + 1); m = strlen(b + 1);
memset(p, 0, sizeof p); memset(ex, 0, sizeof ex);
p[1] = m; int k = 0;
rep(i, 2, m) {
int L = p[i - k + 1], R = k + p[k] - i;
if(L < R) p[i] = L;
else {
cmax(R, 0);
while(i + R <= m && b[i + R] == b[R + 1]) R++;
p[i] = R; if(i + p[i] > k + p[k]) k = i;
}
}
k = 0;
FOR(i, n) {
int L = p[i - k + 1], R = k + ex[k] - i;
if(L < R) ex[i] = L;
else {
cmax(R, 0);
while(i + R <= n && a[i + R] == b[R + 1]) R++;
ex[i] = R; if(i + ex[i] > k + ex[k]) k = i;
}
pr1(ex[i]);
}
}
M a n a c h e r Manacher Manacher算法(马拉车)
首先,回文串长度的奇偶会影响求解方法。为了方便,我们在每个字符两边插入一个
#
\#
#(其他符号也行)。
显而易见的,这是更方便的。如
a
b
a
b
a
−
>
#
a
#
b
#
a
#
b
#
a
#
ababa->\#a\#b\#a\#b\#a\#
ababa−>#a#b#a#b#a#
求解思路
我们定义一个叫做回文半径的东西,用于表示以一个点为中心的回文串的边界到中心的点的总数,以第
i
i
i个点为中心的回文半径为
p
[
i
]
p[i]
p[i]。
具体来讲,变化后中间的a的回文半径为6,原来中间的a的回文半径为3.
(
以下
p
[
i
]
中的
i
均指变化后的第
i
个位置
以下p[i]中的i均指变化后的第i个位置
以下p[i]中的i均指变化后的第i个位置)
可以发现变化后的字符串的最长回文串长度为
max
(
p
[
i
]
)
−
1
\max(p[i])-1
max(p[i])−1.
证明:
根据定义可推出以
i
i
i为中心的回文串长度为
p
[
i
]
∗
2
−
1
p[i]*2-1
p[i]∗2−1.
很明显,两端一定是
#
\#
#. 并且
#
\#
#比字母数多1.
总字母数则为
(
p
[
i
]
∗
2
−
1
−
1
)
/
2
=
p
[
i
]
−
1
(p[i]*2-1-1)/2=p[i]-1
(p[i]∗2−1−1)/2=p[i]−1。
以上我们讲解了如何求正确答案,下面介绍如何用最快的方法求 p p p.
定义 p o s pos pos为以该点为中心的回文串右端点最右的点, r 为最右右端点的下一个位置 r为最右右端点的下一个位置 r为最右右端点的下一个位置(细细体会)
在某个时刻,
p
o
s
,
r
pos,r
pos,r可能是这样的:
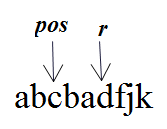
case 1:
我们根据回文串的轴对称性质,可以发现当一个点位于 ( p o s , r ) (pos,r) (pos,r)区间时 (如第二个b),它可以继承关于 p o s pos pos的对称点的回文半径(且可以保证第二个b的回文半径不小于第一个b的)
其实只有两种情况:
case 1.1:

注:
j
为
i
的对称点
,
j
=
2
∗
p
o
s
−
i
(
中点公式
)
,
红线可以看作是一个回文串
j为i的对称点,j=2*pos-i(中点公式),红线可以看作是一个回文串
j为i的对称点,j=2∗pos−i(中点公式),红线可以看作是一个回文串
注意:
r
=
p
o
s
+
p
[
p
o
s
]
(右端点的下一个位置)
r=pos+p[pos](右端点的下一个位置)
r=pos+p[pos](右端点的下一个位置)
当以
j
j
j为中心的回文串的左端点大于以
p
o
s
pos
pos为中心的回文串的左端点(下面用
l
l
l代替,注意
l
,
r
并非关于
p
o
s
的对称点
l,r并非关于pos的对称点
l,r并非关于pos的对称点)时,可以保证
p
[
i
]
=
p
[
j
]
p[i]=p[j]
p[i]=p[j].
为什么?因为
a
[
j
−
p
[
j
]
]
≠
a
[
j
+
p
[
j
]
]
a[j-p[j]]\ne a[j+p[j]]
a[j−p[j]]=a[j+p[j]].根据对称性可知是正确的.(需要自己摸索一下)
case 1.2:
若
j
−
p
o
s
[
j
]
≤
l
j-pos[j]\le l
j−pos[j]≤l,如果
i
i
i直接继承,以
i
为中心的回文串的右端点一定会不小于
r
i为中心的回文串的右端点一定会不小于r
i为中心的回文串的右端点一定会不小于r.
但是
r
r
r右边的世界是不能保证的,所以必须暴力拓展.
case 2:
当 i i i不小于 r r r,暴力判断即可.
复杂度证明:
这个算法的复杂度为
O
(
N
)
O(N)
O(N).
为什么?因为主要复杂度在于
r
r
r的拓展,但是
r
r
r的移动次数始终为
n
n
n,所以复杂度为
O
(
N
)
O(N)
O(N).
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=22e6+10;
char a[N];
int n,p[N],ans;
void Manacher()
{
n=strlen(a+1);
for(int i=n;i>=1;i--)a[i*2]=a[i],a[i*2-1]='#';
n=n<<1|1;a[n]='#';
int pos=0,r=0;ans=0;
for(int i=1;i<=n;i++)
{
if(i<r)p[i]=min(p[2*pos-i],r-i);
else p[i]=1;
while(i-p[i]>0&&a[i-p[i]]==a[i+p[i]])p[i]++;
if(i+p[i]>r)pos=i,r=i+p[i],ans=max(ans,p[i]-1);
}
printf("%d\n",ans);
}
int main() {
while(~scanf("%s",a+1))Manacher();
return 0;
}
T r i e Trie Trie:
字典树
Trie一般指字典树
又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
Trie树太简单了 ,我就只给个复杂度吧:
O
(
总字符数
)
O(总字符数)
O(总字符数)
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int trie[N][26],tot=1,cnt[N];
void ins(char *s) {
int len=strlen(s),p=1;
for(int i=0;i<len;i++) {
char c=s[i]-'a';
if(!trie[p][c])trie[p][c]=++tot;
p=trie[p][c];cnt[p]++;
}
}
int search(char *s) {
int len=strlen(s),p=1;
for(int i=0;i<len;i++) {
p=trie[p][s[i]-'a'];
if(!p)break;
}
return cnt[p];
}
char s[15];
int main() {
int n,m;
scanf("%d",&n);
while(n--)scanf("%s",s),ins(s);
scanf("%d",&m);
while(m--)
scanf("%s",s),printf("%d\n",search(s));
return 0;
}
A C AC AC自动机:
前言:
如果你会自动AC机,那还要学AC自动机干什么.
前置芝士: K M P 及 T r i e 树 KMP及Trie树 KMP及Trie树
(学了它们可以更加方便地学习AC自动机)
不同与KMP这种单模匹配算法,AC自动机可是多模匹配的哦~~
思路:
考虑暴力:
设模式串有
n
n
n个,分别为
s
1
,
s
2
,
s
3
.
.
.
.
.
.
.
.
s
n
s_1,s_2,s_3........s_n
s1,s2,s3........sn,长度为别为
b
1
,
b
2
,
b
3
.
.
.
.
.
.
.
b
n
(
b
1
≤
b
2
≤
b
3
≤
.
.
.
.
.
≤
b
n
)
,
b_1,b_2,b_3.......b_n(b_1\le b_2\le b_3 \le .....\le b_n),
b1,b2,b3.......bn(b1≤b2≤b3≤.....≤bn),
a
为长度为
m
的匹配串
a为长度为m的匹配串
a为长度为m的匹配串
对于一个位置
i
i
i,考虑以
i
i
i结尾有没有出现单词。即:
(
注:
p
d
为比较
)
(注:pd为比较)
(注:pd为比较)
p
d
(
a
[
i
−
b
1
+
1
∼
i
]
,
s
1
)
pd(a[i-b_1+1 \sim i],s_1)
pd(a[i−b1+1∼i],s1)
p
d
(
a
[
i
−
b
2
+
1
∼
i
]
,
s
2
)
pd(a[i-b_2+1 \sim i],s_2)
pd(a[i−b2+1∼i],s2)
p
d
(
a
[
i
−
b
3
+
1
∼
i
]
,
s
3
)
pd(a[i-b_3+1 \sim i],s_3)
pd(a[i−b3+1∼i],s3)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.....................
.....................
复杂度非常可观:
O
(
m
2
n
)
O(m^2n)
O(m2n)(复杂度都是估大的)
考虑优化:
其实世上本没有算法,暴力继承的判断多了,也便成了算法。
由上面可以看出如果以一个位置
i
i
i为结尾,这个字符串的后缀没有单词(模版串),这样pd就会很低效。
同时,如果以
i
i
i为结尾的后缀为某些单词的前缀的话,那么就可以直接继承。
现在开始正式学习AC自动机。
一波定义:
学习了 T r i e Trie Trie树以后,我们设 s x s_x sx表示编号为x的 T r i e Trie Trie树节点到根这条路径所代表的字符串。(其实就是某个模版串的前缀。)
若 f a i l x = y fail_x=y failx=y,则表示 s x s_x sx的非前缀后缀为 s y s_y sy,并且 l e n ( s y ) 最大 len(s_y)最大 len(sy)最大。(如果找不到y,则y为根(代码中根为1))
举个小栗子:
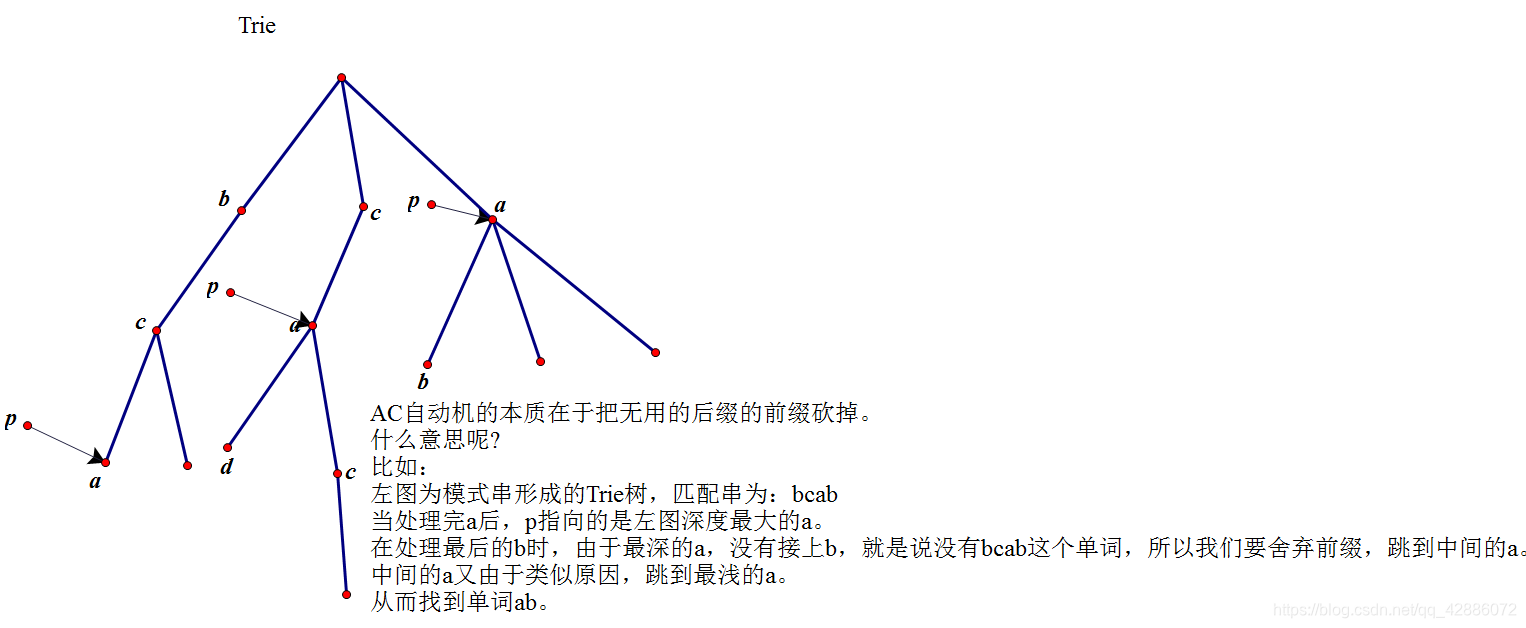
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=5e5+10,M=1e6+10;
int trie[N][26],fail[N],ed[N],tot;//相比于Trie树,只多了个fail
int T,n,ans;
char s[M];
void ins() {
int len=strlen(s),p=0;
for(int i=0;i<len;i++) {
char c=s[i]-'a';
if(!trie[p][c])trie[p][c]=++tot;
p=trie[p][c];
}
ed[p]++;
}
int q[N],l,r;
void bfs() {
l=r=1;q[1]=0;
while(l<=r) {
int p=q[l++];
for(int c=0,x,y;c<26;c++) {
if(!trie[p][c])continue;
x=trie[p][c];
if(p) {
y=fail[p];
while( y && !trie[y][c] )y=fail[y];//s[y](上面有定义)每次变化量尽可能小。
fail[x]=trie[y][c];//把根设为0就可以减少特判
}
q[++r]=x;
}
}
}
void search() {
ans=0;
int len=strlen(s),p=0,q;
for(int i=0;i<len;i++) {
char c=s[i]-'a';
while( p && !trie[p][c] )p=fail[p];//AC自动机优秀就在于它能把无用的后缀的前缀砍掉。
p=trie[p][c];q=p;
while(q) {
ans+=ed[q];
ed[q]=0;
q=fail[q];
}
}
printf("%d\n",ans);
}
int main() {
scanf("%d",&T);
while(T--) {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%s",s),ins();
bfs();
scanf("%s",s);search();
tot=(tot+1)<<2;
memset(trie,0,tot*26);
memset(fail,0,tot);
memset(ed ,0,tot);
tot=0;
}
return 0;
}
复杂度分析
这个算法的复杂度为
O
(
模式串总字符数
∗
字符集大小
)
O(模式串总字符数*字符集大小)
O(模式串总字符数∗字符集大小).
其实最迷的地方在于:
void bfs() {
q[l=r=1]=0;
while(l<=r) {
int p=q[l++];
for(int c=0,x,y;c<26;c++) {
if(!(x=trie[p][c])) continue;
if(p) {
y=fail[p];
while(y&&!trie[y][c]) y=fail[y];
fail[x]=trie[y][c];
ed[x]|=ed[fail[x]];
}
else fail[x]=0;
q[++r]=x;
}
}
}
while(y&&!trie[y][c]) y=fail[y];
这难道不是
O
(
t
o
t
2
)
O(tot^2)
O(tot2)的吗?
如果你这么想就错了------我们假设所有模式串不交.
然后对于每个模式串(设长度为
l
e
n
len
len)对应
T
r
i
e
Trie
Trie树节点(
x
x
x)的
f
a
i
l
fail
fail指针进行分析.
fail[x]=trie[y][c];
很明显
r
o
o
t
−
−
>
x
的
f
a
i
l
指针合计进行了
l
e
n
次如上操作
,
深度增加了
l
e
n
.
root-->x的fail指针合计进行了len次如上操作,深度增加了len.
root−−>x的fail指针合计进行了len次如上操作,深度增加了len.
又因为
f
a
i
l
指针每次都要继承父节点的且每跳一次
f
a
i
l
至少减一
又因为fail指针每次都要继承父节点的且每跳一次fail至少减一
又因为fail指针每次都要继承父节点的且每跳一次fail至少减一
综上
:
r
o
o
t
−
−
>
x
的与
f
a
i
l
相关的复杂度为
O
(
l
e
n
)
,
每个
T
r
i
e
树节点复杂度均摊
O
(
1
)
综上:root-->x的与fail相关的复杂度为O(len),每个Trie树节点复杂度均摊O(1)
综上:root−−>x的与fail相关的复杂度为O(len),每个Trie树节点复杂度均摊O(1)
证毕!
后缀数组( S A SA SA):
一个望尘莫及的
b
l
o
g
blog
blog
另一个望尘莫及的
b
l
o
g
blog
blog
定义:
s u f f i x [ i ] 表示以第 i 个位置开头的后缀 , 下面简称后缀 i suffix[i]表示以第i个位置开头的后缀,下面简称后缀i suffix[i]表示以第i个位置开头的后缀,下面简称后缀i
s a [ i ] 表示排序后排名为 i 的为后缀几 ( 可理解为第 i 小是谁 ) sa[i]表示排序后排名为i的为后缀几(可理解为第i小是谁) sa[i]表示排序后排名为i的为后缀几(可理解为第i小是谁)
r k [ i ] 表示后缀 i 排名为几 ( 可理解为我排第几大 ) rk[i]表示后缀i排名为几(可理解为我排第几大) rk[i]表示后缀i排名为几(可理解为我排第几大)
根据定义可以发现: s a [ r k [ i ] ] = r k [ s a [ i ] ] = i sa[rk[i]]=rk[sa[i]]=i sa[rk[i]]=rk[sa[i]]=i.
w v [ i ] 表示后缀 i 前缀的大小 ( 通过离散化可求 ) wv[i]表示后缀i前缀的大小(通过离散化可求) wv[i]表示后缀i前缀的大小(通过离散化可求)
c 是桶 , 用于基数排序 c是桶,用于基数排序 c是桶,用于基数排序
后缀排序:
DA(倍增大法):
一句话概括:每个后缀先以第一个字符排序,再以前两个字符排序,再以前四个字符排序……
具体来讲,先求出每个后缀第一个字符的大小(即 a s c i i 码 ascii码 ascii码).按第一个字符排序.
接着,可以发现后缀 i i i的第二个字符就是后缀 i + 1 i+1 i+1的第一个字符,我们把它当作第二关键字进行排序,并求出每个后缀的前两个字符的相对大小(用离散化求)
第三次,我们拍每个后缀的前4个位置,每个后缀
i
i
i有两个关键字
(
x
[
i
]
,
x
[
i
+
2
]
(
x
[
i
]
为后缀
i
取前
2
两个字符得到的大小
x[i],x[i+2](x[i]为后缀i取前2两个字符得到的大小
x[i],x[i+2](x[i]为后缀i取前2两个字符得到的大小)).
之后,以此类推……
贴一张罗穗骞大神的图:
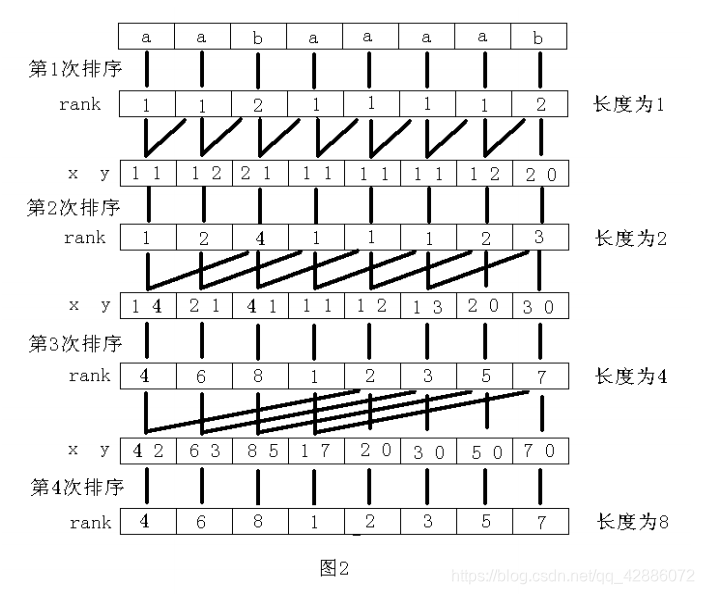
代码恶心,需耐心食用。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=11e5+10;
void write(int x) {
if(x/10)write(x/10);
putchar(x%10+'0');
}
char r[N];
int wa[N],wb[N],wv[N],c[N],sa[N],n,m;
void DA() {
int i,j,p,*x=wa,*y=wb;//只是交换指针比交换数组快得多。
x[n+1]=y[n+1]=0;
for(i=1;i<=n;i++)++c[x[i]=r[i]];
for(i=2;i<=m;i++)c[i]+=c[i-1];
for(i=n;i>=1;i--)sa[c[x[i]]--]=i;//预处理出单个字符的排位
for(j=1,p=1;p<n;j=j<<1,m=p) {//m=p,表示桶的大小更新
p=0;//y[i]表示第二关键字排名为i的数,第一关键字的位置。
for(i=n-j+1;i<=n;i++)y[++p]=i;//当前处理的是每个后缀的前j*2个字符。[n-j+1,n]的压根没有第二关键字,第一关键字的位置就是自身的位置。
for(i=1;i<=n;i++)if(sa[i]>j)y[++p]=sa[i]-j;//sa在上一重循环已经按当前的第二关键字排序了。从小到大枚举可以保证第二关键字大的在后面。
for(i=1;i<=n;i++)wv[i]=x[y[i]];//wv为第一关键字,x[i]其实存的是[i,i+j-1]的数离散出来的值
for(i=1;i<=m;i++)c[i]=0;//清空桶
for(i=1;i<=n;i++)c[wv[i]]++;
for(i=2;i<=m;i++)c[i]+=c[i-1];
for(i=n;i>=1;i--)sa[c[wv[i]]--]=y[i];//按第一关键字排序
swap(x,y);p=1;x[sa[1]]=1;//把原来的值倒到y,求出新的离散值。
for(i=2;i<=n;i++)//离散化——求出下一次的第一关键字
x[sa[i]]=(y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+j]==y[sa[i]+j])?p:++p;
//由于&&的短路性质,我们这样写是能够保证不会RE的。(所以我并不能出到令代码RE的数据)
//现在其实是在处理每个后缀的前2*j个位置的离散化任务。当后缀不足2*j长度时,是能够自动补0的。
}
for(i=1;i<=n;i++)write(sa[i]),putchar(' ');
}
int main() {
scanf("%s",r+1);
n=strlen(r+1);m=122;//'z'的ascii码为122
DA();
return 0;
}
DC3算法
这个算法是 O ( n ) O(n) O(n)的,但是常数较大,编程复杂度较高,在不卡常的题目上还是用倍增好.
算法流程:
- 先把一部分后缀进行排序.(不被3整除的后缀)
- 对剩下的后缀进行排序.
比较两个后缀:
1. s u f f i x [ i ∗ 3 ] = s [ i ∗ 3 ] + r k [ i ∗ 3 + 1 ] , s u f f i x [ j ∗ 3 + 1 ] = s [ j ∗ 3 + 1 ] + r k [ i ∗ 3 + 2 ] suffix[i*3]=s[i*3]+rk[i*3+1],suffix[j*3+1]=s[j*3+1]+rk[i*3+2] suffix[i∗3]=s[i∗3]+rk[i∗3+1],suffix[j∗3+1]=s[j∗3+1]+rk[i∗3+2]
2. s u f f i x [ i ∗ 3 ] = s [ i ∗ 3 ] + s [ i ∗ 3 + 1 ] + r k [ i ∗ 3 + 2 ] , s u f f i x [ j ∗ 3 + 2 ] = s [ j ∗ 3 + 2 ] + s [ j ∗ 3 + 3 ] + r k [ ( j + 1 ) ∗ 3 + 1 ] suffix[i*3]=s[i*3]+s[i*3+1]+rk[i*3+2],suffix[j*3+2]=s[j*3+2]+s[j*3+3]+rk[(j+1)*3+1] suffix[i∗3]=s[i∗3]+s[i∗3+1]+rk[i∗3+2],suffix[j∗3+2]=s[j∗3+2]+s[j∗3+3]+rk[(j+1)∗3+1] - 合并结果.
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e6+10,M=3*N;
#define F(x) ((x)/3+((x)%3==1?0:tb))//余1的扔左边,余2的扔右边(tb为余1的个数哦~~)
#define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)//G,F互为反函数.
char r[N];
int n,m,a[M],sa[M],wa[N],wb[N],wv[N],c[N];
//————————递归需要,a,sa要开3倍哦~~~ !!!!!!!!!!!——————
bool c0(int *r,int a,int b) {//判断两个字符组是否相同
return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];
}
bool c12(int k,int *r,int a,int b) {//比较两个后缀的大小
if(k==2) return r[a]<r[b]||(r[a]==r[b]&&c12(1,r,a+1,b+1));
return r[a]<r[b]||(r[a]==r[b]&&wv[a+1]<wv[b+1]);
}
void sort(int *r,int *a,int *b,int n,int m) {//基数排序
register int i;//b是后缀数组,a是按第二关键字排序的第一关键字位置
for(i=0;i<n;i++) wv[i]=r[a[i]];
for(i=0;i<m;i++) c[i]=0;
for(i=0;i<n;i++) c[wv[i]]++;
for(i=1;i<m;i++) c[i]+=c[i-1];
for(i=n-1;i>=0;i--) b[--c[wv[i]]]=a[i];
}
void DC3(int *r,int *sa,int n,int m) {
register int i,j,p,ta=0,tb=(n+1)/3,tbc=0,*x=wa,*y=wb,*rn=r+n,*san=sa+n;
r[n]=r[n+1]=0;//结尾自动补0
//把所有的%3!=0的分成一类先处理
for(i=1;i<n;i++) if(i%3) y[tbc++]=i;
for(i=2;i>=0;i--)//字符组(3个字符)中越后的优先级越小
sort(r+i,y,x,tbc,m),swap(x,y);
for(p=1,rn[F(y[0])]=0,i=1;i<tbc;i++)//把余1和余2的分开(F函数)(以下简述为左右块),
//又因为r[n]=r[n+1]=0,所以比较两个后缀时,比较所需的最短前缀的端点一定不会跨两块.
//而新数组rn上,在一块上连续的一段数也必然能映射为原串的子串. (这使得我们可以利用上面的结果)
rn[F(y[i])]=c0(r,y[i-1],y[i])?p-1:p++;//对字符组进行离散化
if(p^tbc) DC3(rn,san,tbc,p);
else for(i=0;i<tbc;i++) san[rn[i]]=i;//已经分出大小了,当然就不用递归啦
//开始处理被3整除的位置
for(i=0;i<tbc;i++) if(san[i]<tb) y[ta++]=san[i]*3;//这里按顺序扫.因为之后我们把第一关键字设为3的倍数,第二关键字设为紧接着的余1的后缀
if(n%3==1) y[ta++]=n-1;//n-1没有后缀,所以上面不会加它
sort(r,y,x,ta,m);
for(i=0;i<tbc;i++) wv[y[i]=G(san[i])]=i;//构造名次数组.
//简单的归并
for(i=j=p=0;i<ta&&j<tbc;p++)
sa[p]=c12(y[j]%3,r,x[i],y[j])?x[i++]:y[j++];
for( ;i<ta;p++) sa[p]=x[i++];
for( ;j<tbc;p++) sa[p]=y[j++];
}
int main() {
scanf("%s",r);
for(n=0;r[n];n++) a[n]=r[n];
DC3(a,sa,n+1,'z'+1);//加一个最小的值在末尾,防止越界.
for(int i=1;i<=n;i++) printf("%d ",sa[i]+1);
puts(""); return 0;
}
复杂度分析:
T
(
n
)
=
O
(
n
)
+
T
(
n
∗
2
3
)
T(n)=O(n)+T(n*\dfrac{2}{3})
T(n)=O(n)+T(n∗32).
T
(
n
)
=
O
(
n
)
∗
(
1
+
2
3
+
(
2
3
)
2
.
.
.
.
)
=
3
O
(
n
)
T(n)=O(n)*(1+\dfrac{2}{3}+(\dfrac{2}{3})^2....)=3O(n)
T(n)=O(n)∗(1+32+(32)2....)=3O(n)(等比数列求和+忽略小常数)
不可重叠最长重复子串:
这里要引入
h
e
i
g
h
t
,
h
height,h
height,h数组。
h
e
i
g
h
t
[
i
]
表示排名为
i
的后缀与排名为
i
−
1
的后缀的最长公共前缀
height[i]表示排名为i的后缀与排名为i-1的后缀的最长公共前缀
height[i]表示排名为i的后缀与排名为i−1的后缀的最长公共前缀
h
[
i
]
表示后缀
i
与
(
排名上
)
前一个后缀的最长公共前缀
,
即
h
[
i
]
=
h
e
i
g
h
t
[
r
k
[
i
]
]
h[i]表示后缀i与(排名上)前一个后缀的最长公共前缀,即h[i]=height[rk[i]]
h[i]表示后缀i与(排名上)前一个后缀的最长公共前缀,即h[i]=height[rk[i]]
我们可以利用 h 的性质 , 用线性时间跑出 h e i g h t h的性质,用线性时间跑出height h的性质,用线性时间跑出height.
引理1: h [ i ] ≥ h [ i − 1 ] − 1 h[i]\ge h[i-1]-1 h[i]≥h[i−1]−1
设k为(排名上)i-1的前一个后缀.
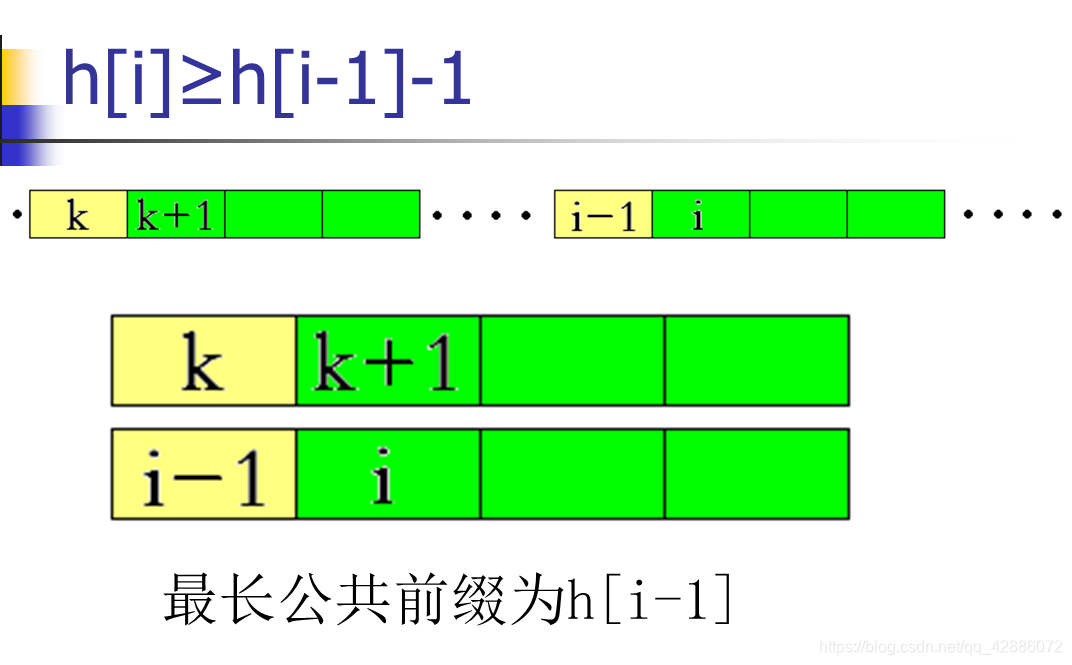

当
h
[
i
−
1
]
≤
1
h[i-1]\le 1
h[i−1]≤1时,显然.
否则,由上图可以看出后缀k+1与后缀i的最长公共前缀至少为h[i-1]-1.
还有一点需要注意的是
r
k
[
k
+
1
]
<
r
k
[
i
]
rk[k+1]<rk[i]
rk[k+1]<rk[i].为什么?因为
r
k
[
k
]
<
r
k
[
i
−
1
]
啊
rk[k]<rk[i-1]啊
rk[k]<rk[i−1]啊
那么又因为在
后缀
s
a
[
i
]
(
i
∈
[
1
,
r
k
[
i
]
)
)
中
后缀sa[i](i\in [1,rk[i]))中
后缀sa[i](i∈[1,rk[i]))中,与
后缀
i
后缀i
后缀i最相似的一定是后缀
s
a
[
r
k
[
i
]
−
1
]
sa[rk[i]-1]
sa[rk[i]−1],
所以可以保证的是
L
C
P
(
s
a
[
i
]
,
s
a
[
r
k
[
i
]
−
1
]
)
≥
L
C
P
(
s
a
[
i
]
,
k
+
1
)
LCP(sa[i],sa[rk[i]-1])\ge LCP(sa[i],k+1)
LCP(sa[i],sa[rk[i]−1])≥LCP(sa[i],k+1)(LCP为最长公共前缀)
证毕!
求height:
void calcheight() {
for(int i=1;i<=n;i++)rk[sa[i]]=i;
for(int i=1,k=0,j;i<=n;height[rk[i++]]=k)
for((k?k--:0),j=sa[rk[i]-1];a[i+k]==a[j+k];k++);//i+k由1扫到n——O(n)
}
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20010;
int wa[N],wb[N],wv[N],c[N],sa[N],a[N],rk[N],height[N],n,m;
void DA() {
int i,j,p,*x=wa,*y=wb;
x[n+1]=y[n+1]=0;
for(i=1;i<=m;i++)c[i]=0;
for(i=1;i<=n;i++)c[x[i]=a[i]]++;
for(i=2;i<=m;i++)c[i]+=c[i-1];
for(i=n;i>=1;i--)sa[c[x[i]]--]=i;
for(j=1,p=1;p<n;j=j<<1,m=p) {
for(p=0,i=n-j+1;i<=n;i++)y[++p]=i;
for(i=1;i<=n;i++)if(sa[i]>j)y[++p]=sa[i]-j;
for(i=1;i<=n;i++)wv[i]=x[y[i]];
for(i=1;i<=m;i++)c[i]=0;
for(i=1;i<=n;i++)c[wv[i]]++;
for(i=2;i<=m;i++)c[i]+=c[i-1];
for(i=n;i>=1;i--)sa[c[wv[i]]--]=y[i];
swap(x,y);p=1;x[sa[1]]=1;
for(i=2;i<=n;i++)
x[sa[i]]=(y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+j]==y[sa[i]+j])?p:++p;
}
}
void calcheight() {
for(int i=1;i<=n;i++)rk[sa[i]]=i;
for(int i=1,k=0,j;i<=n;height[rk[i++]]=k)
for((k?k--:0),j=sa[rk[i]-1];a[i+k]==a[j+k];k++);//i+k由1扫到n——O(n)
}
bool check(int k) {//找两段长度不小于k的相同子串,并且保证子串不相邻
int l,r;l=r=sa[1];
for(int i=2;i<=n;i++) {
if(height[i]<k)l=r=sa[i];
else {
if(sa[i]>r) {
r=sa[i];
if(r-l>k)return 1;
}
else if(sa[i]<l) {
l=sa[i];
if(r-l>k)return 1;
}
}
}
return 0;
}
void solve() {
int l=3,r=n>>1,mid;
while(l<r) {
mid=(l+r+1)>>1;
if(check(mid))l=mid;
else r=mid-1;
}
if(l==3)puts("0");
else printf("%d\n",l+1);
}
int main() {
while(scanf("%d",&n),n) {
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
--n;for(int i=1;i<=n;i++)a[i]=a[i+1]-a[i]+100;//允许转调,那么两段数的主题相同,则差分数组中的这两段数(忽略开头位置)相同。
m=200;DA();calcheight();solve();
}
return 0;
}
后缀自动机( S A M SAM SAM)
前言:
入门这个数据结构,首先需要养好肝。
然后,牺牲花两天的空闲时间。
最后,光荣去世。
正题:
推荐blog:
以下为瞎扯,可自行忽略
首先,定义
e
n
d
p
o
s
(
s
)
为
s
endpos(s)为s
endpos(s)为s串在原串中的结束位置组成的集合。
例如:原串为“abbab”,s为“ab",则
e
n
d
p
o
s
(
s
)
=
{
2
,
5
}
endpos(s)=\{2,5\}
endpos(s)={2,5}。
我们把
e
n
d
p
o
s
endpos
endpos相同的子串集定义为
e
n
d
p
o
s
endpos
endpos等价类。定义
l
e
n
(
a
)
等价类
a
中最长子串的长度
len(a)等价类a中最长子串的长度
len(a)等价类a中最长子串的长度.
例如上面的原串,有一个等价类
a
为
{
"
a
b
b
a
"
,
"
b
b
a
"
,
"
b
a
"
}
,
则
l
e
n
(
a
)
=
4
a为\{"abba","bba","ba"\},则len(a)=4
a为{"abba","bba","ba"},则len(a)=4
后缀自动机本质上就是对子串按等价类进行压缩。下面所说的“一个状态”对应一个 e n d p o s endpos endpos等价类。
下面给出一些引理:
-
若子串a为b的后缀,则有: e n d p o s ( b ) ⊆ e n d p o s ( a ) endpos(b)\subseteq endpos(a) endpos(b)⊆endpos(a)。
这个引理显然是成立的。凡是b出现的地方都有a,但有可能a出现的次数更多。同时, a 是 b 的后缀当且仅当 e n d p o s ( a ) ⊇ e n d p o s ( b ) a是 b的后缀当且仅当 endpos(a)⊇endpos(b) a是b的后缀当且仅当endpos(a)⊇endpos(b), a 不是 b 的后缀当且仅当 e n d p o s ( a ) ∩ e n d p o s ( b ) = ∅ . a不是 b的后缀当且仅当 endpos(a)∩endpos(b)=∅. a不是b的后缀当且仅当endpos(a)∩endpos(b)=∅. ( 可用反证法证明,但其实感性理解即可 ) (可用反证法证明,但其实感性理解即可) (可用反证法证明,但其实感性理解即可)
-
S A M 中一个状态包含的子串都互为后缀。 SAM中一个状态包含的子串都互为后缀。 SAM中一个状态包含的子串都互为后缀。
-
对于一个 e n d p o s endpos endpos等价类中所有的子串,按长度排序后,则长度连续,且长度较短的为长度较长的子串的后缀。
后缀链接
知道了引理3,可以发现等价类中的子串的长度是连续的,但有时会断开。
即一个等价类的子串的长度集合可能为
{
5
,
4
,
3
}
\{5,4,3\}
{5,4,3}.
又例如:“abbab”,一个状态的最长子串为"abba",和“abba"同一等价类的有
{
"
b
b
a
"
,
"
b
a
"
}
\{"bba","ba"\}
{"bba","ba"}
但是”a”不属于这个等价类,因为
e
n
d
p
o
s
(
"
a
"
)
=
{
1
,
4
}
,
e
n
d
p
o
s
(
"
b
a
"
)
=
{
4
}
endpos("a")=\{1,4\}, endpos("ba")=\{4\}
endpos("a")={1,4},endpos("ba")={4}.
我们定义“abba”对应的状态的后缀链接指向“a“对应的状态。
如果我们把后缀链接看成一条有向边,则SAM为一棵有根树。(这棵树又被称为 p a r e n t parent parent树)
状态集合
对于一个状态,它所能形成的状态构成它的状态集合。
有图有真相

如果我们把状态到新状态看成一条有向边,则SAM为一个DAG(有向无环图)
从根到任意节点形成的路径表示的串为该状态的对应串.(一个状态可以对应多个串)
构造SAM:
复杂度证明
数组版: 时间复杂度
O
(
∣
S
∣
)
O(|S|)
O(∣S∣). 空间复杂度
O
(
∣
S
∣
∣
C
∣
)
O(|S||C|)
O(∣S∣∣C∣)
m
a
p
map
map版: 时间复杂度
O
(
∣
S
∣
log
∣
C
∣
)
O(|S|\log |C|)
O(∣S∣log∣C∣). 空间复杂度
O
(
∣
S
∣
)
O(|S|)
O(∣S∣).
模板题
传送门
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=250010;
struct node {
int len,link,v[27];
}tr[N<<1];
int n,last,tot,a[N],f[N],r[N<<1],c[N],sa[N<<1];
char s[N];
void ins(int c) {
int p=last,x=last=++tot;tr[x].len=tr[p].len+1;
for( ;p&&!tr[p].v[c];p=tr[p].link)tr[p].v[c]=x;
if(!p)tr[x].link=1;
else {
int q=tr[p].v[c],y;
if(tr[p].len+1==tr[q].len)tr[x].link=q;
else {
tr[y=++tot]=tr[q];//复制一遍
tr[y].len=tr[p].len+1;
tr[q].link=tr[x].link=y;
for( ;p&&tr[p].v[c]==q;p=tr[p].link)tr[p].v[c]=y;
}
}
}
int main() {
last=tot=1;
scanf("%s",s+1);n=strlen(s+1);
for(int i=1;i<=n;i++)ins(a[i]=s[i]-'a');
for(int i=1,p=1;i<=n;i++)r[p=tr[p].v[a[i]]]++;//因为一个子串一定是某个前缀的后缀,所以先给前缀对应的位置打上标记。
for(int i=1;i<=tot;i++)c[tr[i].len]++;
for(int i=2;i<=n;i++)c[i]+=c[i-1];
for(int i=1;i<=tot;i++)sa[c[tr[i].len]--]=i;//基数排序
for(int i=tot;i>=1;i--)r[tr[sa[i]].link]+=r[sa[i]];//给前缀的后缀打上标记
for(int i=1;i<=tot;i++)f[tr[i].len]=max(f[tr[i].len],r[i]);
for(int i=1;i<=n;i++)printf("%d\n",f[i]);
return 0;
}
补充性质
- 在 p a r e n t parent parent树(由后缀链接形成的树)上 x , y 的 L C A x,y的LCA x,y的LCA为最长公共后缀对应的状态.
- SAM维护多个串信息的根号技巧
有 n n n个串,第 i i i个串的长度为 l e n i len_i leni,令 S = ∑ l e n i S=\sum len_i S=∑leni.
如果我们要维护类似子串在多少个不同的串中出现过 这样的信息.
对于每个串,我们每加入一个字符以后就暴力跳后缀连接更新未被当前串更新过的 S A M SAM SAM节点.
S A M SAM SAM的总节点数上界为 2 S − 1 2S-1 2S−1,而单次如果按后缀连接长度来计算覆盖节点的话,那么单串的复杂度为 min ( 2 S − 1 , l e n i 2 ) \min(2S-1,len_i^2) min(2S−1,leni2).
可以发现当 l e n i ≤ 2 S len_i \le \sqrt{2S} leni≤2S 时复杂度较大,复杂度上界为 O ( S S ) O(S \sqrt S) O(SS) .(这种做法实际上并不好卡,所以可以表现得比 log S \log S logS更快).
广义后缀自动机
简单理解就是多串后缀自动机.
例题
下面推荐两种实用方法.
在线版
#include<map>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#include<cctype>
#include<vector>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lc (x<<1)
#define rc (x<<1|1)
#define gc getchar()//(p1==p2&&(p2=(p1=buf)+fread(buf,1,size,stdin),p1==p2)?EOF:*p1++)
#define mk make_pair
#define pi pair<int,int>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=2e6+10,size=1<<20;
//char buf[size],*p1=buf,*p2=buf;
template<class o> void qr(o &x) {
char c=gc; x=0; int f=1;
while(!isdigit(c)){if(c=='-')f=-1; c=gc;}
while(isdigit(c)) x=x*10+c-'0',c=gc;
x*=f;
}
template<class o> void qw(o x) {
if(x/10) qw(x/10);
putchar(x%10+'0');
}
template<class o> void pr1(o x) {
if(x<0)x=-x,putchar('-');
qw(x); putchar(' ');
}
template<class o> void pr2(o x) {
if(x<0)x=-x,putchar('-');
qw(x); puts("");
}
int n,last=1,tot=1; char s[N];ll ans;
struct node{int fa,len,v[26];}tr[N];
void add(int c) {
int p=last;
if(tr[p].v[c]) {
int q=tr[p].v[c],y;
if(tr[p].len+1==tr[q].len) last=q;
else {
tr[last=y=++tot]=tr[q];//需要分裂
tr[y].len=tr[p].len+1;
tr[q].fa=y;
for( ;p&&tr[p].v[c]==q;p=tr[p].fa) tr[p].v[c]=y;
}
}
else {
int x=last=++tot; tr[x].len=tr[p].len+1;
for( ;p&&tr[p].v[c]==0;p=tr[p].fa) tr[p].v[c]=x;
if(!p) tr[x].fa=1;
else {
int q=tr[p].v[c],y;
if(tr[p].len+1==tr[q].len) tr[x].fa=q;
else {
tr[y=++tot]=tr[q];
tr[y].len=tr[p].len+1;
tr[q].fa=tr[x].fa=y;
for( ;p&&tr[p].v[c]==q;p=tr[p].fa) tr[p].v[c]=y;
}
}
}
}
int main() {
qr(n); while(n--) {
scanf("%s",s+1); last=1;
for(int i=1;s[i];i++) add(s[i]-'a');
}
for(int i=2;i<=tot;i++) ans+=tr[i].len-tr[tr[i].fa].len;
pr2(ans);
return 0;
}
离线版
#include<map>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lc (x<<1)
#define rc (x<<1|1)
#define gc getchar()//(p1==p2&&(p2=(p1=buf)+fread(buf,1,size,stdin),p1==p2)?EOF:*p1++)
#define mk make_pair
#define pi pair<int,int>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=2e6+10,size=1<<20;
//char buf[size],*p1=buf,*p2=buf;
template<class o> void qr(o &x) {
char c=gc; x=0; int f=1;
while(!isdigit(c)){if(c=='-')f=-1; c=gc;}
while(isdigit(c)) x=x*10+c-'0',c=gc;
x*=f;
}
template<class o> void qw(o x) {
if(x/10) qw(x/10);
putchar(x%10+'0');
}
template<class o> void pr1(o x) {
if(x<0)x=-x,putchar('-');
qw(x); putchar(' ');
}
template<class o> void pr2(o x) {
if(x<0)x=-x,putchar('-');
qw(x); puts("");
}
char s[N];
namespace SAM {
int tot=1;
struct node{int fa,len,v[26];}tr[N];
int add(int last,int c) {
int p=last,x=last=++tot; tr[x].len=tr[p].len+1;
for( ;p&&tr[p].v[c]==0;p=tr[p].fa) tr[p].v[c]=x;
if(!p) tr[x].fa=1;
else {
int q=tr[p].v[c],y;
if(tr[p].len+1==tr[q].len) tr[x].fa=q;
else {
tr[y=++tot]=tr[q];
tr[y].len=tr[p].len+1;
tr[q].fa=tr[x].fa=y;
for( ;p&&tr[p].v[c]==q;p=tr[p].fa) tr[p].v[c]=y;
}
}
return last;
}
void solve() {
ll ans=0;
for(int i=2;i<=tot;i++) ans+=tr[i].len-tr[tr[i].fa].len;
pr2(ans);
}
}
namespace Trie {
int trie[N][26],cnt=1,fa[N]; char type[N];
void ins() {
int p=1;
for(int i=1,c;s[i];i++) {
c=s[i]-'a';
if(!trie[p][c]) fa[trie[p][c]=++cnt]=p,type[cnt]=c;
p=trie[p][c];
}
}
int q[N],pos[N];
void bfs() {
int l=1,r=0;
pos[1]=1;
for(int c=0;c<26;c++) if(trie[1][c]) q[++r]=trie[1][c];
while(l<=r) {
int x=q[l++];
pos[x]=SAM::add(pos[fa[x]],type[x]);
for(int c=0;c<26;c++) if(trie[x][c]) q[++r]=trie[x][c];
}
}
}
int main() {
int n; qr(n); while(n--) {
scanf("%s",s+1);
Trie::ins();
}
Trie::bfs(); SAM::solve();
return 0;
}
小结:
在线和离线在随机情况下速度差不多,但是离线的空间要大1倍.
当数据的前缀重叠较多时,离线算法的优秀性就会凸显.(
T
r
i
e
Trie
Trie树保证了前缀相同只算一次)
回文自动机 P A M PAM PAM
例题:求一个字符串中本质不同的回文子串数量.
如果不是要求本质不同的话,我们跑一遍 M a n a c h e r Manacher Manacher,那么答案就是 ∑ p − 1 \sum p-1 ∑p−1.
正文
我们类比
T
r
i
e
Trie
Trie树,把所有的回文子串给联系起来.
即
t
r
[
x
]
[
c
]
=
y
tr[x][c]=y
tr[x][c]=y相当于
x
x
x所对应的串两边+
c
c
c=
y
y
y所对应的串.
例如
x
−
>
"
a
b
a
"
,
c
=
′
c
′
,
则
y
−
>
"
c
a
b
a
c
"
x->"aba",c='c',则y->"cabac"
x−>"aba",c=′c′,则y−>"cabac".
这样根到点的路径即可表示一个回文子串.(类似
T
r
i
e
Trie
Trie树).
点与回文子串可以构成双射.
那你可能有个问题,这样好像只能处理偶数长度的串,那奇数长的呢?
为了解决这个问题,我们
P
A
M
PAM
PAM有两个根,一个奇根,一个偶根.
一些定义:
l e n [ x ] len[x] len[x]表示 x x x对应串的长度
f a i l [ x ] fail[x] fail[x]表示 x x x对应串的最长非本身回文后缀的对应状态.(类似AC自动机中的运用)
l a s t last last表示已加入字符串的最长回文后缀对应的状态
t o t tot tot为节点数
设偶根为0,奇根为1.
l
e
n
[
0
]
=
0
,
l
e
n
[
1
]
=
−
1
len[0]=0,len[1]=-1
len[0]=0,len[1]=−1
对于非空串(对应状态非0/1),若无非本身回文后缀则
f
a
i
l
=
0
fail=0
fail=0
特别地,
f
a
i
l
[
0
]
=
1
,
f
a
i
l
[
1
]
随意
fail[0]=1,fail[1]随意
fail[0]=1,fail[1]随意.
算法流程:
- 设当前加入字符为 c c c
- 找到 l a s t last last对应串的满足可添加 c c c的回文后缀对应状态 p p p.
- 若 t r [ p ] [ c ] = 0 tr[p][c]=0 tr[p][c]=0,新建一个状态 x x x,依次进行: l e n [ x ] = l e n [ p ] + 2 , 求 f a i l [ x ] , t r [ p ] [ c ] = x len[x]=len[p]+2,求fail[x],tr[p][c]=x len[x]=len[p]+2,求fail[x],tr[p][c]=x
- 最后 l a s t = t r [ p ] [ c ] last=tr[p][c] last=tr[p][c].
由第3点我们可以发现出奇根的巧妙性.
无封装代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=3e5+10;
char s[N];
int fail[N],tr[N][26],len[N],last,tot;
int Find(int x,int n) {//找到一个状态x,它的两边可以加上一个字符s[n].
while(s[n-len[x]-1]^s[n]) x=fail[x];
return x;
}
int main() {
scanf("%s",s+1);
s[0]=-1; fail[0]=1;
len[0]=0; len[1]=-1;
last=tot=1;
for(int i=1,p,x,c;s[i];i++) {
c=s[i]-'a';
p=Find(last,i);
if(!tr[p][c]) {
len[x=++tot]=len[p]+2;
fail[x]=tr[Find(fail[p],i)][c];
//因为tr的初值为0,所以找不到会合法的后缀时fail[x]会指向0
tr[p][c]=x;
//这里之所以后操作,你模拟一下只有一个字符'a'的情况就知道了.
}
last=tr[p][c];
}
printf("%d\n",tot-1); return 0;//除去奇根
}
一些性质/注意
- 在 F i n d Find Find函数中, x = 1 x=1 x=1时一定可以求解完成,所以不必设 f a i l [ 1 ] fail[1] fail[1].
- t r tr tr初值为0,也就使得无回文后缀时 f a i l [ x ] = 0 fail[x]=0 fail[x]=0
- 失配后先跑到 0 0 0,而不是 1 1 1,是为了回文后缀的最长,先尝试长度为2,最后不行就一定是1.
- s [ 0 ] s[0] s[0]要设为不会出现的值,如上面的-1.
- 根据整个算法流程可以证明:长度为 n n n的串最多有 n n n个本质不同的串.
无封装版容易出现变量重复且看起来有点乱,所以建议把代码封装到 n a m e s p a c e 或 s t r u c t namespace或struct namespace或struct内.
封装版代码:
换一道题有
l y n d o n lyndon lyndon 分解
对一个串
s
s
s, 把其分解为
s
1
,
s
2
,
.
.
.
,
s
m
s_1,s_2,...,s_m
s1,s2,...,sm使得
s
i
≥
s
i
+
1
s_i\ge s_{i+1}
si≥si+1.
其中的每个串
s
i
s_i
si我们称其为
Lyndon Word
\text{Lyndon Word}
Lyndon Word. 每个
Lyndon Word
\text{Lyndon Word}
Lyndon Word 满足最小后缀为本身。
code:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5e6 + 10;
int n, ans;
char s[N];
void lyndon(char *s, int n) {
for(int i = 1, j, k; i <= n; ) {
j = i; k = i + 1;
while(k <= n && s[j] <= s[k])
if(s[j] ^ s[k++]) j = i;//合并
else j++; //匹配增加
k = k - j; // period
while(i <= j) {
i += k;
ans ^= i - 1;//右端点
}
}
printf("%d\n", ans);
}
int main() {
scanf("%s",s + 1); n = strlen(s + 1);
lyndon(s, n);
return 0;
}





 本文深入讲解了多种核心算法,包括KMP算法、exKMP算法、Manacher算法、Trie树、AC自动机、后缀数组、后缀自动机、广义后缀自动机、回文自动机以及Lyndon分解,提供了详细的实现代码和复杂度分析。
本文深入讲解了多种核心算法,包括KMP算法、exKMP算法、Manacher算法、Trie树、AC自动机、后缀数组、后缀自动机、广义后缀自动机、回文自动机以及Lyndon分解,提供了详细的实现代码和复杂度分析。

















 1154
1154

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










