Minimax Triangulation UVA - 1331 最优三角剖分

题目链接

 对于一个n个顶点的凸多边形，有很多种方法可以对它进行三角剖分（triangulation），即用n－3条互不相交的对角线把凸多边形分成n－2个三角形。为每个三角形规定一个权函数w(i, j, k)（如三角形的周长或3个顶点的权和），求让所有三角形权和最大的方案。
【分析】
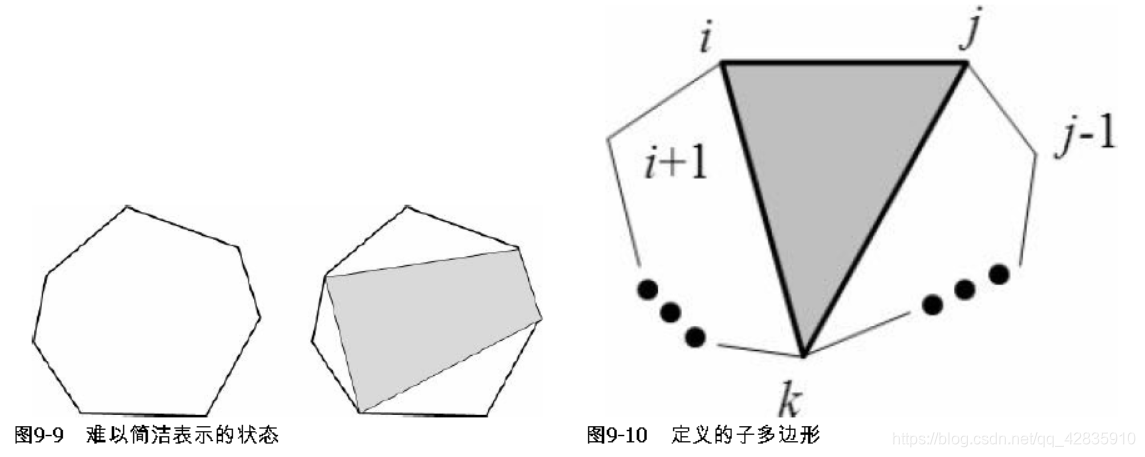
本题和最优矩阵链乘问题十分相似，但存在一个显著不同：链乘表达式反映了决策过程，而剖分不反映决策过程。举例来说，在链乘问题中，方案((A1A2)(A3(A4A5)))只能是先把序列分成A1A2和A3A4A5两部分，而对于一个三角剖分，“第一刀”可以是任何一条对角线，如图9-9所示。如果允许随意切割，则“半成品”多边形的各个顶点是可以在原多边形中随意选取的，很难简洁定义成状态，而“矩阵链乘”就不存在这个问题——无论怎样决策，面临的子问题一定可以用区间表示。在这样的情况下，有必要把决策的顺序规范化，使得在规范的决策顺序下，任意状态都能用区间表示。定义d(i, j)为子多边形i, i＋1,…, j－1, j（i＜j）的最优值，则边i－j在最优解中一定对应一个三角形i－j－k（i＜k＜j），如图9-10所示（注意顶点是按照逆时针编号的）。

因此，状态转移方程为：
时间复杂度为O(n3)，边界为d(i,i＋1)=0，原问题的解为d(0,n－1)。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
 
using namespace std;
const int N = 100;
const double INF = 0x3f3f3f3f3f3f;
const double eps = 1e-9;
 
struct point {
	double x, y;
	void get() {
		scanf("%lf%lf", &x, &y);
	}
}p[N];
 
int n;
double dp[N][N];
 
double area (point a, point b, point c) {
	return fabs((b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y))/2;
}
 
bool judge (int a, int b, int c) {
	double cur = area(p[a], p[b], p[c]);
	for (int i = 0; i < n; i++) {
		if (i == a || i == b || i == c)
			continue;
		double tmp = area(p[a], p[b], p[i]) + area(p[b], p[c], p[i]) + area(p[c], p[a], p[i]);
		if (fabs(tmp - cur) < eps)
			return false;
	}
	return true;
}
 
double solve () {
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < n; j++)
			dp[j][(j+i)%n] = 0;
	}
 
	for (int i = 0; i < n; i++)
		dp[i][(i+2)%n] = area(p[i], p[(i+1)%n], p[(i+2)%n]);
 
	for (int k = 3; k < n; k++) {
 
		for (int i = 0; i < n; i++) {
			int t = (i + k) % n;
			dp[i][t] = INF;
			for (int j = (i+1)%n; j != t; j = (j+1)%n) {
				if (judge(i, t, j))
					dp[i][t] = min(dp[i][t], max(max(dp[i][j], dp[j][t]), area(p[i], p[j], p[t])));
			}
		}
	}
 
	double ans = INF;
	for (int i = 0; i < n; i++)
		ans = min (ans, dp[i][(i+n-1)%n]);
	return ans;
}
 
int main () {
	int cas;
	scanf("%d", &cas);
	while (cas--) {
		scanf("%d", &n);
		for (int i = 0; i < n; i++)
			p[i].get();
 
		printf("%.1lf\n", solve());
	}
	return 0;
}