补题记录-BZOJ 1912: [Apio2010]patrol 巡逻(求树的直径+拓展)

##98kai想进WF##
题目链接：https://www.lydsy.com/JudgeOnline/problem.php?id=1912

题目：

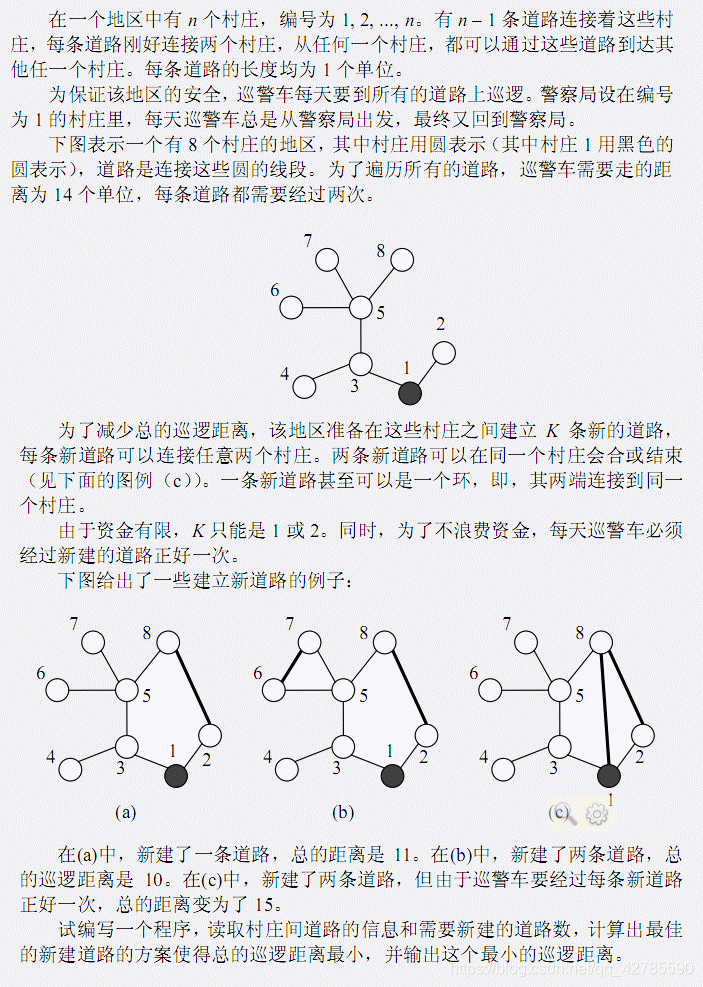
Input
第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1行，每行两个整数 a, b， 表示村庄a与b之间有一条道路(1 ≤ a, b ≤ n)。
Output
输出一个整数，表示新建了K 条道路后能达到的最小巡逻距离。

Sample Input
8 1
1 2 	
3 1 
3 4 
5 3 
7 5 
8 5 
5 6 
Sample Output
11

思路：

首先考虑k=1的情况，k=1时，只需要在原来的树上找直径l1，然后新的路径就是连接距离最长得两个点即可。这样，原本直径上的边需要每条边走两遍，此时加上这条路径以后，只需要走一遍即可。那么，就有ans=2*(n-1)-(l1-1)，其中l1是树的直径。
再考虑k=2的情况，k等于2的时候，那么很容易想到，只需要找两边直径就行了。但是中间有一些细节。第一遍找到直径以后，需要把第一次找的直径上的边的权值改为-1，然后再次找修改权值以后的数的直径l2，那么答案就是ans=2*(n-1)-(l1+1)-(l2+1)。需要注意的是，当树上边权存在负数时，只能用dp来找直径，用两遍bfs找数的直径是错的。其中样例中如果k=2，就是一个两边bfs出错的例子。
那做法有了，为什么第二遍找直径的时候要把第一次找的直径上所有的边权改为-1呢？由于题目要求每一条边至少走一遍，并且新的边只能走一遍，那么，第二次加边的时候，由于每加一条边都会产生一个环。第一次加了边以后，所形成的环上所有的路径都从走两遍变成了走一遍。如果第二次加的边所形成的环中的某些变也存在于第一次加的边所形成的环，那么这些边经过的次数又会-1，就不会经过这些边了。但是由于每条边至少走一遍，所以为了走这些边，不得不再去走一遍这些边，然后再回来，直接导致这些边走的次数又变成了两次。所以考虑到这种情况，就把这些边的权值改为-1即可。

代码实现：

dp求直径，并且还要记录直径的两个端点s1，s2还是比较麻烦，细节（坑点）也比较多，我就是自己认为是这么写，但是没有证明正确性，不过既然AC了，应该也对了吧。
AC代码：

// #include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<iomanip>
#include<ostream>
#include<cstring>
#include<string.h>
#include<string>
#include<cstdio>
#include<cctype>
#include<vector>
#include<cmath>
#include<queue>
#include<set>
#include<stack>
#include<map>
#include<cstdlib>
#include<time.h>
#include<bitset>
#define pb push_back
#define _fileout freopen("out.txt","w",stdout)
#define _filein freopen("in.txt","r",stdin)
#define test(i) printf("ok%d\n",i)
using namespace std;
typedef double db;
typedef long long ll;
const double PI = acos(-1.0);
const ll MOD=1e9+7;
const ll MAXN=2e5+10;
const int INF=0x3f3f3f3f;
const ll ll_INF=9223372036854775807;
ll qm(ll a,ll b){ll ret = 1;while(b){if (b&1)ret=ret*a%MOD;a=a*a%MOD;b>>=1;}return ret;}
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return (a*b)/gcd(a,b);}
int head[MAXN],nexts[MAXN];//数组表示邻接表。（不懂的可以先去学习一下）
int s[MAXN],e[MAXN],w[MAXN];//分别表示第i条边的起点，终点和权值
int last[MAXN];//记录dp过程中离i节点距离最长得点是哪个点
int d[MAXN];//记录以i节点为根的树的深度是多少
int vis[MAXN];//记录点i是否被访问过
int n,k;
int s1,s2;//s1,s2这两个，表示dp过程中最长路径是由哪两个点的相加而来的
int ans;//这个好像没有卵用，全程等于2*（n-1）
int l1,mid,l2;//l1,l2好像也没有卵用，不过还是定义了，方便理解，l1是k=1的时候直径，l2是k=2时的直径
int pre[MAXN];//修改图的边权时用到的数组，表示目前这个点是由哪一个点得到的
int tot;//数组表示邻接表时，维护边的数量
void add(int x,int y)//增加边
{
	s[++tot]=x;e[tot]=y;w[tot]=1;
	nexts[tot]=head[x];
	head[x]=tot;
}
void update()//修改图的边权，把第一次最长路径经过的环上的边权由1改为-1.
{
	memset(vis,0,sizeof(vis));
	queue<int>q;
	q.push(s1);
	while(!q.empty())
	{
		int x=q.front();
		vis[x]=1;
		q.pop();
		for(int i=head[x];i;i=nexts[i])
		{
			int y=e[i];
			if(vis[y])continue;
			pre[y]=x;
			q.push(y);
		}
	}
	int x=s2;
	while(x!=s1)
	{
		for(int i=head[x];i;i=nexts[i])
		{	
			int y=e[i];
			if(y==pre[x])
			{
				for(int j=head[y];j;j=nexts[j])//这里主要，由于边是双向的，所以要把来回的边都修改一下。（其实是一条边，但是我们存了两个，具体看邻接表）
				{
					if(e[j]==x)
					{
						w[j]=-1;
						break;
					}
				}
				w[i]=-1;
				x=y;
				break;
			}
		}
	}

}
void  dp(int x)//寻找树的直径。
{
	vis[x]=1;
	for(int i=head[x];i;i=nexts[i])
	{
		int y=e[i];
		if(vis[y])continue;
		dp(y);
		if(mid<d[x]+d[y]+w[i])
		{
			s1=last[x],s2=last[y];
			mid=d[x]+d[y]+w[i];
		}
		if(d[x]<d[y]+w[i])
		{
			last[x]=last[y];
			d[x]=d[y]+w[i];
		}
	}
	return;
}
void init()//初始化数组
{
	for(int i=1;i<=n;i++)
	{
		last[i]=i;
		d[i]=0;
		vis[i]=0;
	}
	s1=s2=1;
	mid=0;
}
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	ans=2*(n-1);
	init();
	dp(1);
	for(int i=1;i<+n;i++)//判断特殊情况，即图的直径是从1开始的一条链，其中i是一个端点，last【i】是另外一个端点。
	{
		if(d[i]==mid)
		{
			s1=i;
			s2=last[i];
			break;
		}
	}
	// printf("s1=%d s2=%d\n",s1,s2);
	l1=mid;
	if(k==1)
	{
		printf("%d",ans-(l1-1));
	}
	else
	{
		update();
		// for(int i=1;i<=n;i++)
		// {
		// 	for(int j=head[i];j;j=nexts[j])
		// 		printf("x=%d y=%d z=%d\n",i,e[j],w[j]);
		// }
		init();
		dp(1);
		l2=mid;
		printf("%d",ans-(l1-1)-(l2-1));
	}
	return 0;
}