反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 :
输入:["h","e","l","l","o"]
输出:["o","l","l","e","h"]
相关标签:双指针 字符串
#pragma once
#includeusing std::vector;
class Solution {
public:
//by myself(双指针)
void reverseString(std::vector& s) {
auto first = s.begin();
auto last = s.end() - 1;
while (first < last) {
std::iter_swap(first, last);
first++; last--;
}
}
};
整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 :
输入:x = 123
输出:321
提示:
- -231 <= x <= 231 - 1
相关标签:数学
#pragma once
#include#includeusing std::vector;
class Solution {
public:
//数学
int reverse(int x) {
int x_ = 0; //定义x_保存最后反转后的结果
while (x != 0) { //每次循环获取x个位上的数,之后再去除这位数,直到所以数取完
if (x_ > INT_MAX / 10) { //判断是否满足题意反转后的数是否超出范围(详情见下方注释)
return 0;
}
int digit = x % 10; //获取个位数
x /= 10; //去除个位数
x_ = x_ * 10 + digit; //循环累加得到最后的数
}
return x_;
}
};
注:
解题思路:
首先我们想一下,怎么去反转一个整数?
用栈?或者把整数变成字符串,再去反转这个字符串?
这两种方式是可以,但并不好。实际上我们只要能拿到这个整数的 末尾数字 就可以了。
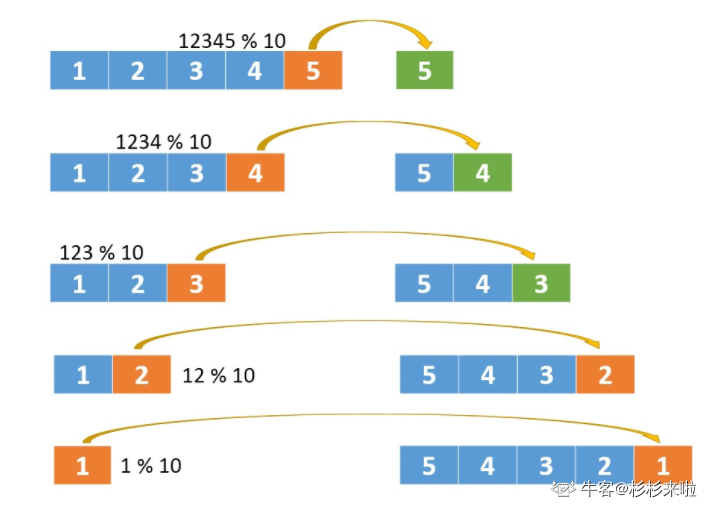
以12345为例,先拿到5,再拿到4,之后是3,2,1,我们按这样的顺序就可以反向拼接处一个数字了,也就能达到 反转 的效果。
怎么拿末尾数字呢?好办,用取模运算就可以了。



字符串中的第一个唯一字符
给定一个字符串,找到它的第一个不重复的字符,并返回它的索引。如果不存在,则返回 -1。
示例:
输入: "loveleetcode"
输出:2
提示:你可以假定该字符串只包含小写字母。
相关标签:哈希表 字符串
#pragma once
#include<string>
#include<iterator>
#include<unordered_map>
#include<queue>
using std::string;
class Solution {
public:
int firstUniqChar(string s) {
/*by myself(使用哈希表存储频数)
std::unordered_map<char, int>hash; //定义一个hash表,键用来存字符串对应位置的字符,值用来存该字符出现次数
for (auto i = s.begin(); i != s.end(); ++i) { //遍历字符串,将其中的字符加入到haah表中,若字符重复出现则对应值++
if (hash.find(*i) == hash.end()) {
hash.insert(std::unordered_map<char, int>::value_type(*i, 1));
}
else {
hash[*i]++;
}
}
for (auto i = s.begin(); i != s.end(); ++i) { //按照字符串中字符顺序查找hash表,若找到的字符对应出现次数为1,则返回该字符的下标
if (hash[*i] == 1) {
return std::distance(s.begin(), i);
}
}
return -1; //执行到这说明字符串中的字符都重复过,所以返回-1;
*/
/*(语法上的简化版本)
std::unordered_map<char, int>hash;
for (char ch : s) {
++hash[ch]; //这一句的作用:对应元素存在就将值hash[ch]+1,不存在就将对应元素插入,值hash[ch]默认为0
}
for (int i = 0; i < s.size(); ++i) {
if (hash[s[i]] == 1) {
return i;
}
}
return -1;
*/
/* 使用hash表存储下标索引
std::unordered_map<char, int>hash; //定义hash表存储字符串中对应字符和下标
for (int i = 0; i < s.size(); ++i) { //遍历字符串,将其中的字符存储到哈希表中
if (hash.count(s[i])) { //如果hash.count[s[i]] != 0,则表示重复出现,将其下标设为-1。否则表示第一次出现,将其小标设置为i
hash[s[i]] = -1;
}
else {
hash[s[i]] = i;
}
}
int first = s.size(); //之后需要做的是在hash表中对应找出,在字符串中的第一个唯一字符。
for (auto x: hash) { //遍历整个hash表,如果对应元素的value!=-1且value<first(表示该唯一字符在更前面),则first设置为value(下标)
if (x.second != -1 && x.second < first) {
first = x.second;
}
}
if (first == s.size()) { //遍历完整个hash后,比较first是否为初始化值s.size(),如果是,表示没有找到唯一数组(因为s.size()大于所有字符下标,如果存在唯一字符,则first一定被覆盖)
return -1;
}
return first;
*/
//队列+hash表(使用hash表存储下标索引,用队列来顺序筛选符合条件的第一个唯一字符)
std::unordered_map<char, int>hash;
std::queue<std::pair<char, int>>que;
for (int i = 0; i < s.size(); ++i) { //遍历整个字符串,如果hash表中对应字符串中的字符没有出现过,则将字符和下标作为元素加入hash表并且插入队列尾部,否则表示重复出现,则在hash表中将该字符对应的下标设置为-1
if (!hash.count(s[i])) {
hash[s[i]] = i;
que.emplace(s[i], i);
}
else {
hash[s[i]] = -1;
}
}
while (!que.empty() && hash[que.front().first] == -1) { //检查队列头部元素存储的对应字符在hash表对应的下标是否等于-1,如果等于表示该元素不是唯一字符,则弹出队列,直到检查到队列中下一个元素满足条件或者队列为空后退出循环
que.pop();
}
return que.empty() ? -1 : que.front().second; //如果队列为空,表示不存在唯一字符,否则返回队列头部元素存储的对应字符的下标
}
};
注:
借助队列找到第一个不重复的字符。队列具有「先进先出」的性质,因此很适合用来找出第一个满足某个条件的元素。
在维护队列时,我们使用了「延迟删除」这一技巧。也就是说,即使队列中有一些字符出现了超过一次,但它只要不位于队首,那么就不会对答案造成影响,我们也就可以不用去删除它。只有当它前面的所有字符被移出队列,它成为队首时,我们才需要将它移除。
有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 :
输入: s = "anagram", t = "nagaram"
输出: true
说明:
你可以假设字符串只包含小写字母。
相关标签:排序 哈希表
#pragma once
#include<string>
#include<algorithm>
#include<unordered_map>
using std::string;
class Solution {
public:
bool isAnagram(string s, string t) {
/*by myself(排序)
if (s.size() != t.size()) { //先比较下长度,长度不同肯定不满足条件
return false;
}
std::sort(s.begin(), s.end()); //将俩个字符串排序
std::sort(t.begin(), t.end());
return s == t; //如果满足条件的话,排序后的俩个字符串应该相同
*/
/*by myself(哈希表)
if (s.size() != t.size()) { //首先判断字符串长度是否相等
return false;
}
std::unordered_map<char, int>hash; //定义一个哈希表用来存储字符串中的字符和对应的频数
for (auto x : s) { //首先遍历字符串s,将字符串中的字符信息统计到hash表中
if (!hash.count(x)) {
hash[x] = 1;
}
else {
hash[x]++;
}
}
for (auto x : t) { //再遍历字符串t,相反,再利用字符串t中对应字符来消除原hash表中对字符串s中字符的统计
if (!hash.count(x)) {
return false;
}
else {
hash[x]--;
if (hash[x] == 0) { //如果对应字符value等于0(出现次数),则删除这个表项
hash.erase(x);
}
}
}
return hash.empty() ? true : false; //如果满足题意条件,那么最后hash表应该为空(字符串t和s中的字符相抵消)
*/
//用数组实现hash表(更快)
if (s.size() != t.size()) {
return false;
}
std::vector<int>table(26, 0); //由于字符串只包含26个小写字母,因此我们可以维护一个长度为26的频次数组table
for (auto x : s) { //因为26个小写字母的ASCLL码值是连续的,正好可以被用来放在长度为26的数组中索引
table[x - 'a']++; //先遍历字符串s中对应字符出现的次数(小技巧:可以将字符x-'a'得到的结果正好对应数组下标0-25)
}
for (auto x : t) { //再遍历字符串t,相反,根据字符串t中字符出现的次数 相应的减去table中对应字符出现的频数
table[x - 'a']--;
if (table[x - 'a'] < 0) { //妙处(利用俩字符串的对等性,满足题意时table中所有元素都应该为0,如果不满足题意,就会一定会导致table中存在元素value<0,从而直接返回false,这一步可以在循环时检查,而不需要另外循环检查)
return false;
}
}
return true;
}
};
验证回文串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
示例 :
输入: "A man, a plan, a canal: Panama"
输出: true
相关标签:双指针 字符串
#pragma once
#include<iostream>
#include<string>
using std::string;
class Solution {
public:
bool isPalindrome(string s) {
/*by myself(双指针)
auto first = s.begin();
auto last = s.end() - 1;
while (first < last) { //使用双指针从字符串首位两头向中间移动比较,first<last时退出循环
while (first < last && !(('0' <= *first && *first <= '9') || ('a' <= *first && *first <= 'z') || ('A' <= *first && *first <= 'Z'))) { //判断*first和*last是否是字母或者数字,如果不是则相应向前或者向后移动(注:这里也要判断first<last)
first++;
}
while (first < last && !(('0' <= *last && *last <= '9') || ('a' <= *last && *last <= 'z') || ('A' <= *last && *last <= 'Z'))) {
last--;
}
if ('A' <= *first && *first <= 'Z') { //统一将大写字母转为小写字母
*first = (*first) + ('a' - 'A');
}
if ('A' <= *last && *last <= 'Z') {
*last = (*last) + ('a' - 'A');
}
if (*first != *last) { //最后进行判读,如果对应字符不同则返回false
return false;
}
first++;
last--;
}
return true;
*/
//双指针(利用库函数的简化版本)
auto first = s.begin();
auto last = s.end() - 1;
while (first < last) { //使用双指针从字符串首位两头向中间移动比较,first<last时退出循环
while (first < last && !isalnum(*first)) { //判断*first和*last是否是字母或者数字,如果不是则相应向前或者向后移动(注:这里也要判断first<last)
first++;
}
while (first < last && !isalnum(*last)) {
last--;
}
if (first < last) { //注:这里再判断一次,因为上面可能因为first不小于last退出循环,此时first==last,但其实在这没影响,如果出现这种情况说明回文中字母和数组单数,且除了最中间那个字符其他都是围绕这个字符对称,也满足条件
if (tolower(*first) != tolower(*last)) {
return false;
}
}
first++;
last--;
}
return true;
}
};
tolower 函数:如果输入的是小写字母或者其他字符,则不进行转换;如果输入的是大写字母,则将大写字母转换为对应的小写字母。
isalnum 函数:如果参数是数字或字母字符,函数返回非零值,否则返回零值。
字符串转换整数 (atoi)
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
- 读入字符串并丢弃无用的前导空格
- 检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
- 读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
- 将前面步骤读入的这些数字转换为整数(即,"123" -> 123, "0032" -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。
- 如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。
- 返回整数作为最终结果。
注意:
- 本题中的空白字符只包括空格字符 ' ' 。
- 除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例 :
输入:s = "42"
输出:42
输入:s = " -42"
输出:-42
输入:s = "4193 with words"
输出:4193
输入:s = "words and 987"
输出:0
输入:s = "-91283472332"
输出:-2147483648
提示:
- 0 <= s.length <= 200
- s 由英文字母(大写和小写)、数字(0-9)、' '、'+'、'-' 和 '.' 组成
相关标签:数学 字符串
#pragma once
#include<string>
using std::string;
class Solution {
public:
int myAtoi(string s) {
int fu_hao = 1;
int number = 0;
auto i = s.begin();
while (i != s.end() && *i == ' ') { //去除空格
i++;
}
if (i == s.end()) {
return 0;
}
if (*i == '-' || *i == '+') { //判断符号
if (*i == '-') {
fu_hao = -1;
i++;
}
else {
i++;
}
}
while (i != s.end() && isdigit(*i)) { //应该从数字部分开始循环,将字符串中的连续数字转为整数
if ((number > INT_MAX / 10) || (number == INT_MAX / 10 && *i > '7') || (number == INT_MIN / 10 && *i > '8') || (number < INT_MIN / 10)) { //在再次整合之前判断number和INT_MAX/10以及INT_MIN/10的大小关系。如果number大于INT_MAX/10或者小于INT_MIN/10那整合(*i)这个数字之后一定越界;如果number等于INT_MAX/10或者INT_MIN/10,那么需要判断接下来被整合的数字(*i)加上number后是否大于INT_MAX或者小于INT_MAX。(这样判断的好出:number不需要定义为long,定义为int也行)
return number > 0 ? INT_MAX : INT_MIN;
}
number = number * 10 + (*i - '0') * fu_hao;
i++;
}
return number;
}
};
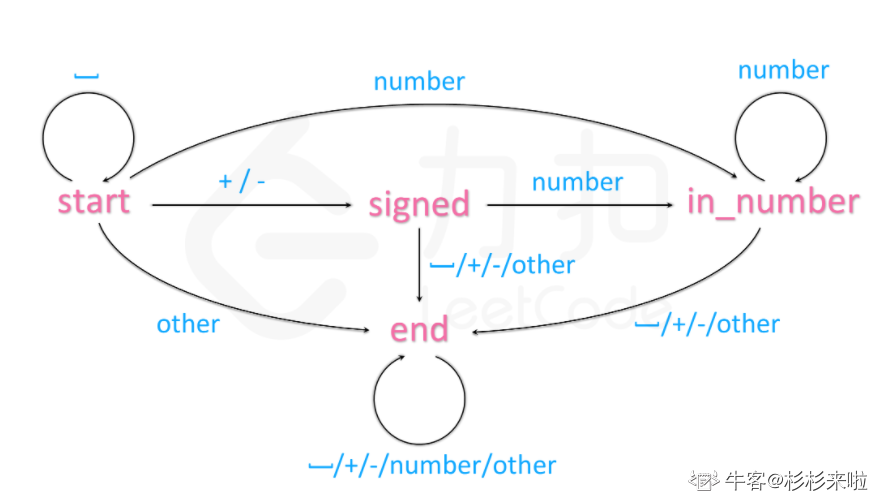
注:字符串处理的题目往往涉及复杂的流程以及条件情况,如果直接上手写程序,一不小心就会写出极其臃肿的代码。因此,为了有条理地分析每个输入字符的处理方法,我们可以使用有限状态机这个概念,根据有限状态机的逻辑关系来编写代码,会更加调理清晰。
实现 strStr()
实现 strStr() 函数。
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串出现的第一个位置(下标从 0 开始)。如果不存在,则返回 -1 。
说明:
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。
示例:
输入:haystack = "hello", needle = "ll"
输出:2
提示:
- 0 <= haystack.length, needle.length <= 5 * 104
- haystack 和 needle 仅由小写英文字符组成
相关标签:双指针 字符串
#pragma once
#include<string>
#include<vector>
#include<iterator>
#include<iostream>
using std::string;
class Solution {
public:
int strStr(string haystack, string needle) {
/*by myself(暴力匹配)
auto iter_h = haystack.begin();
auto iter_n = needle.begin();
if (haystack.size() < needle.size()) { //主串比字串都短肯定不行
return -1;
}
if (needle.empty()) { //子串为空肯定是满足条件
return 0;
}
while (iter_h != haystack.end()) { //遍历主串
if (*iter_h == *iter_n) { //如果主串和子串的迭代器指向的对应字符相同,子串指针向后移动
iter_n++;
}
else { //否则表示这次子串查找失败,得重新从子串第一个字符检查。所以子串迭代器重新设置为begin(),而为了避免重叠错过,这里将主串迭代器回退到最开始匹配子串时指向的下一个位置
iter_h = iter_h - std::distance(needle.begin(), iter_n);
iter_n = needle.begin();
}
iter_h++;
if (iter_n == needle.end()) { //如果子串迭代器iter_n==needle.end()表示子串全部检查完毕,成功匹配
return std::distance(haystack.begin(), iter_h - needle.size()); //在主串中成功匹配子串后,返回子串的第一个字符对应主串中的下标
}
}
return -1;
*/
/*kmp(next中的下标从0开始,next[0]初始值为-1)
if (needle.empty()) { //检查被查找的needle字符串是否为空,如果为空返回0
return -1;
}
std::vector<int>next(needle.size()); //设置next[j]表示位置为j的字符前面的字符串的最长前缀匹配子字符串最后一个字符的下一个字符的位置下标
next[0] = -1; //设置"哨兵",第一个字符前无字符串给值-1(j==-1表示这轮的比较过程中检查到了不匹配字符,表示在这个字符之前的字符都匹配(有的话),且在这个字符之前的字符串中没有匹配的最长前后缀(除了字符串本身),所以重新开始一轮的比较)
int i = 0;
int j = -1; //初始的j=-1设置为"哨兵",表示开始新的一轮的比较
while (i < needle.size() - 1) { //因为next数组中j最大为t.length-1,而每一步next数组赋值都是在j++之后,所以最后一次经过while循环时j为t.length-2
if (j == -1 || needle[i] == needle[j]) { //j==-1表示触发"哨兵",重新开始一轮比较,i向前移动,j+1=0指向起始字符。next[i]=j表示下标i之前的 最长匹配前缀最后一个元素(j-1) 的下一个元素的位置是j。如果j=0,即j-1=-1,表示下标i之前没有最长前缀匹配(位置0之前没有字符)
++i;
++j;
next[i] = j; //这里指 把字符needle[i-1]所在字符串的 最长匹配前缀子字符串最后一个字符(needle[j-1])的下一个字符位置(j)填入到needle[i-1]所在字符串的下一个位置(i)的next中即next[i])。同时做到i,j向后移动从而继续比较,妙。
}
else {
j = next[j]; //next[j]表示该位置j处字符不匹配时应该回溯到的字符的下标,该下标之前的字符串就是最长匹配前缀(前面把最长匹配前缀最后一个字符的下一个位置存在了本次比较的子字符串的下一个位置。而这里正好查找该不匹配元素之前子字符串的最大匹配前缀,且移动到最大匹配前缀的下一个位置,正好对上)
}
}
i = 0;
j = 0;
while (i < haystack.size()) { //遍历整个主字符串
if (j == -1 || haystack[i] == needle[j]) { //j==-1表示触发哨兵,也就是该不匹配字符前的子字符串中没有最长前缀匹配,从而重新开始一轮比较;haystack[i] == needle[j]表示对应字符匹配,i、j都向后移动准备比较下一个字符
++i;
++j;
}
else {
j = next[j]; //表示出现位置j上的字符不匹配,从而寻找位置j之前的子字符串中的最大前缀匹配子子字符串的下一个位置next[j],继续与next[j]指向的字符比较
}
if (j == needle.size()) { //如果j==needle.size()表示匹配成功,needle字符串的所以字符都匹配完毕,返回needle字符串在haystack字符串中首次出现的位置下标
return i - j;
}
}
return -1;
*/
//kmp(next中的下标从1开始,next[0]为默认值0)
if (needle.empty()) { ////检查被查找的needle字符串是否为空,如果为空返回0
return 0;
}
std::vector<int> next(needle.size()); //与上面代码写法不同,设置next[j]表示位置为j的字符 "所在的" 字符串的最长前缀匹配子字符串最后一个字符的下一个字符的位置下标
for (int i = 1, j = 0; i < needle.size(); i++) { //这里默认next[0]为0,也是作为一个"哨兵"作用,needle字符串对应字符从next数组下标1开始,且字符i所在位置的最长匹配前缀存放在当前next[i]下(和上面代码有所不同,上面代码是放在next[i+1]下)
while (j != 0 && needle[i] != needle[j]) { //在这里j=0设置为"哨兵",表示新一轮的比较
j = next[j - 1]; //next[j-1]表示下标j处字符不匹配时应该回溯到的字符的下标,该下标之前的字符串就是最长匹配前缀(上边代码是下标next[j]之前的字符串是最长匹配前缀,是因为他把下标j之前的最长匹配前缀最后一个字符的下一个位置下标填到了next[j],而这里直接填到最长匹配前缀的最后一个字符所在位置,也就是j-1)
}
if (needle[i] == needle[j]) { //haystack[i] == needle[j]表示对应字符匹配,j向后移动准备比较下一个字符(与上面代码不同,这里每个循环都会自增i,所以这里只需要考虑j移动)
j++;
}
next[i] = j; //这里看似和上边代码不同,其实意义相同。上边代码在触发"哨兵"(即寻找最长匹配前缀失败)或者满足needle[i] == needle[j]条件时才执行该语句;在这里,每个循环都必须执行,因为伴随i移动必须要相应填入next[i]的值(这里也是同样存在这两种情况,可以理解为在找最长匹配前缀过程中如果needle[i] == needle[j]则next[i]=[j+1],否则next[i]=0)
}
for (int i = 0, j = 0; i < haystack.size(); i++) { //遍历整个主字符串
while (j != 0 && haystack[i] != needle[j]) { //表示非"哨兵"情况,且haystack[i] != needle[j]时,进行回溯,这里表示回溯到 下标j之前的字符串中的 最长匹配前缀子字符串的最后一个字符的下一个位置下标(上面代码中这个下标是放在所匹配字符串最后一个字符的下一个坐标的next中,即next[j]。而这里是放在所匹配字符串最后一个字符下标对应的next中,即next[j-1])
j = next[j - 1]; //注:这个next作用就是要回溯到 needle[j]之前的字符串的 最大前缀匹配子字符串最后一个字符的下一个位置下标(这个下标在上一个写法代码中是放在next[j]中,在这里是放在next[j-1]中)
}
if (haystack[i] == needle[j]) { //haystack[i] == needle[j]表示对应字符匹配,j向后移动准备比较下一个字符
j++;
}
if (j == needle.size()) { //如果j==needle.size()表示匹配成功,needle字符串的所以字符都匹配完毕,返回needle字符串在haystack字符串中首次出现的位置下标(注:上面那段代码是每次满足haystack[i] == needle[j]后++i、++j,这段代码只是++j。所以上面那段代码是i-j,这段代码是i-j+1)
return i - j + 1;
}
}
return -1; //表示主串haystack中不存在字串
}
};
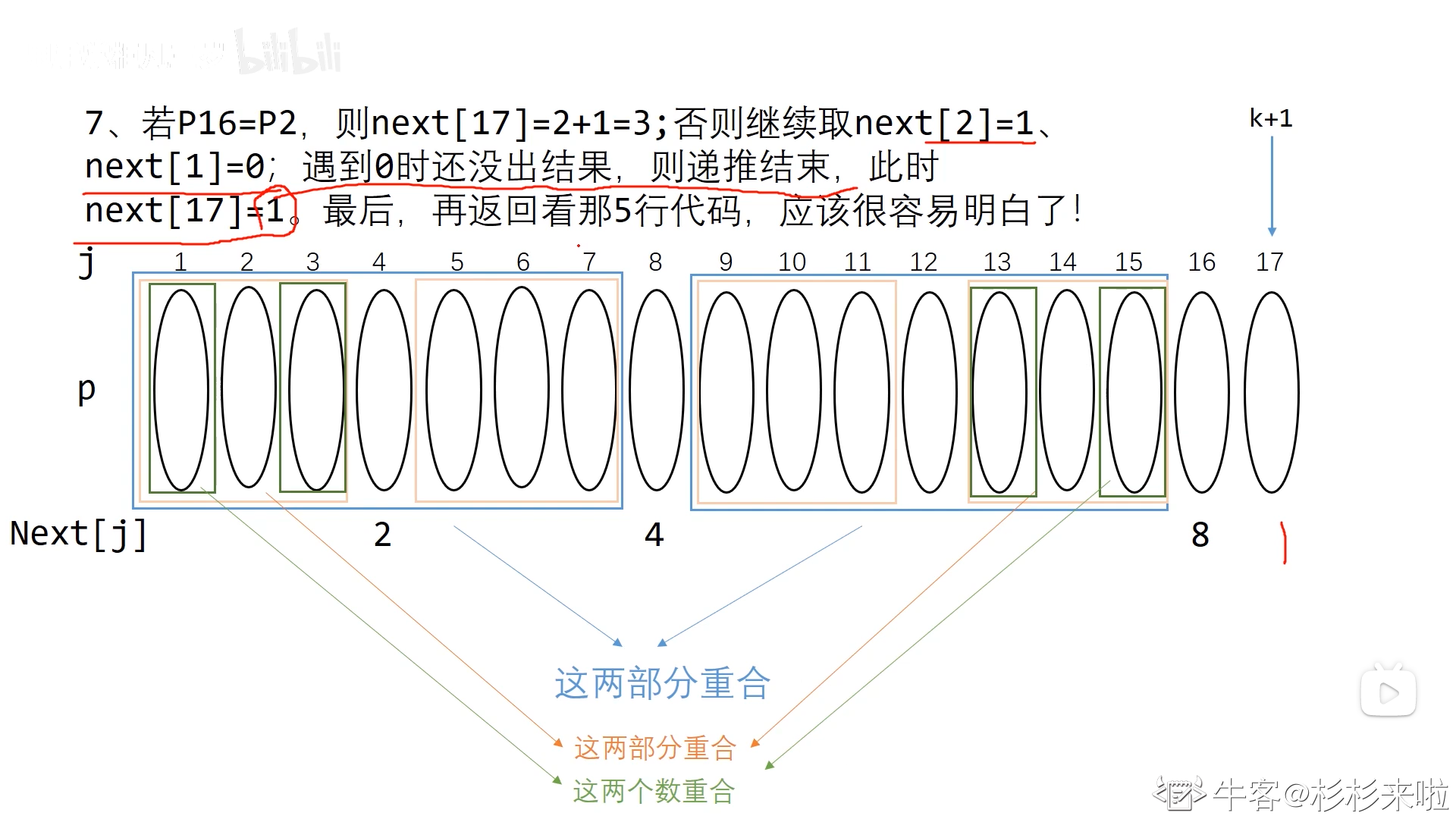
注:根据上图来理解相应字符未匹配后的回溯
外观数列
给定一个正整数 n ,输出外观数列的第 n 项。
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
- countAndSay(1) = "1"
- countAndSay(n) 是对 countAndSay(n-1) 的描述,然后转换成另一个数字字符串。
前五项如下:
1. 1
2. 11
3. 21
4. 1211
5. 111221
第一项是数字 1
描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 "11"
描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 "21"
描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 "1211"
描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 "111221"
要 描述 一个数字字符串,首先要将字符串分割为 最小 数量的组,每个组都由连 相同字符 续的最多组成。然后对于每个组,先描述字符的数量,然后描述字符,形成一个描述组。要将描述转换为数字字符串,先将每组中的字符数量用数字替换,再将所有描述组连接起来。
示例 1:
输入:n = 1
输出:"1"
解释:这是一个基本样例。
示例 2:
输入:n = 4
输出:"1211"
解释:
countAndSay(1) = "1"
countAndSay(2) = 读 "1" = 一 个 1 = "11"
countAndSay(3) = 读 "11" = 二 个 1 = "21"
countAndSay(4) = 读 "21" = 一 个 2 + 一 个 1 = "12" + "11" = "1211"
提示:
- 1 <= n <= 30
相关标签:字符串
#pragma once
#include<iostream>
using std::string;
class Solution {
public:
string countAndSay(int n) {
/* by myself(字符串尾部追加哨兵)
string str = "1 "; //字符串最后面加一个' '用来作为结束标志,字符尾加' '是因为循环结束后,旧序列中排在最后一个的数字虽然被搜到了,但并没有被加入到新序列中,所以字符串尾部再加’'字符,使得多循环一轮,因此最后一个数字得以加入。
string str_t; //str_t为存储新生成序列的字符串
if (n == 1) { //n==1时直接返回'1'本身,而不是'11'(n=2),题目要求。
str.pop_back();
return str;
}
while (n-1) { //按照题意知,这里循环n-1次
int number = 1; //number初始化为1(而不是0,因为每比较成功一个再加上本身就是2个一样的)
char ch = ' '; //定义一个ch用来存储查找 number个ch 时的关键字符ch
for (auto x : str) { //遍历所在轮次的字符串str
if (x == ch) { //如果遍历str中的相应字符x与ch相同时,递增number(表示出现的次数)
number++;
}
else {
if (ch != ' ') { //如果x!=ch且ch遍历到的是有效数字而不是’’,则将number和ch依次插入临时字符串str_t中,表示对ch的查找结束,将number重新置1。如果ch==' '说明有效字符已经遍历完,。且ch!=' '的情况都执行插入,ch==' '为无效不执行插入
str_t.push_back(number + '0');
str_t.push_back(ch);
number = 1;
}
ch = x; //因为ch初始化为’'所以这句要分开放,避免因为初始时ch==' '而执行不到这句
}
}
str_t.push_back(' '); //在str_t尾部插入' '后赋值给str,最后再清空str_t,继续循环
str = str_t;
str_t.clear();
n--;
}
str.pop_back();
return str;
*/
//(思路优化)
string str = "1";
string str_t;
if (n == 1) { //n==1时直接返回'1'本身,而不是'11'(n=2),题目要求。
return str;
}
while (n - 1) { //按照题意知,这里只需循环n-1次
int number = 1; //number初始化为1(而不是0,因为每比较成功一个再加上本身就是2个一样的)
char ch = *(str.begin()); //定义一个ch用来存储查找 number个ch 时的关键字符ch,ch初始化为字符串第一个字符(和上面有差别的地方,这里逻辑上更应该这样做,而不是向上法一样导致额外增加复杂度)
for (auto x = str.begin() + 1; x != str.end(); ++x) { //遍历所在轮次的字符串str,因为第一个字符作为关键字符ch,相当于已经搜过,只要从第二个字符开始
if (*x == ch) { //如果遍历str中的相应字符x与ch相同时,递增计数器number
number++;
}
else { //如果x!=ch,则将number和ch依次插入临时字符串str_t中,表示对当前关键字符ch的查找结束,将number重新置1,ch设置为下一个查找的关键字符ch(即*x)
str_t.push_back(number + '0');
str_t.push_back(ch);
number = 1;
ch = *x;
}
}
str_t.push_back(number + '0'); //(边界处理)注意,旧序列中排在最后一个的数字虽然被搜到了,但是此时已是最后一次循环,所以ch并没有被加入到新序列中,因此要把它也补进去
str_t.push_back(ch);
str = str_t;
str_t.clear();
n--;
}
return str;
}
};
最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"]
输出:"fl"
示例 2:
输入:strs = ["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀。
提示:
- 0 <= strs.length <= 200
- 0 <= strs[i].length <= 200
- strs[i] 仅由小写英文字母组成
相关标签:字符串
#pragma once
#include<algorithm>
#include<string>
#include<vector>
using std::string;
using std::vector;
class Solution {
public:
string longestCommonPrefix_two(const string& str1, const string& str2);
string longestCommonPrefix_fenzhi(const vector<string>& strs, int start, int end);
bool isCommonPrefix(const vector<string>& strs, const int mid);
string longestCommonPrefix(vector<string>& strs) {
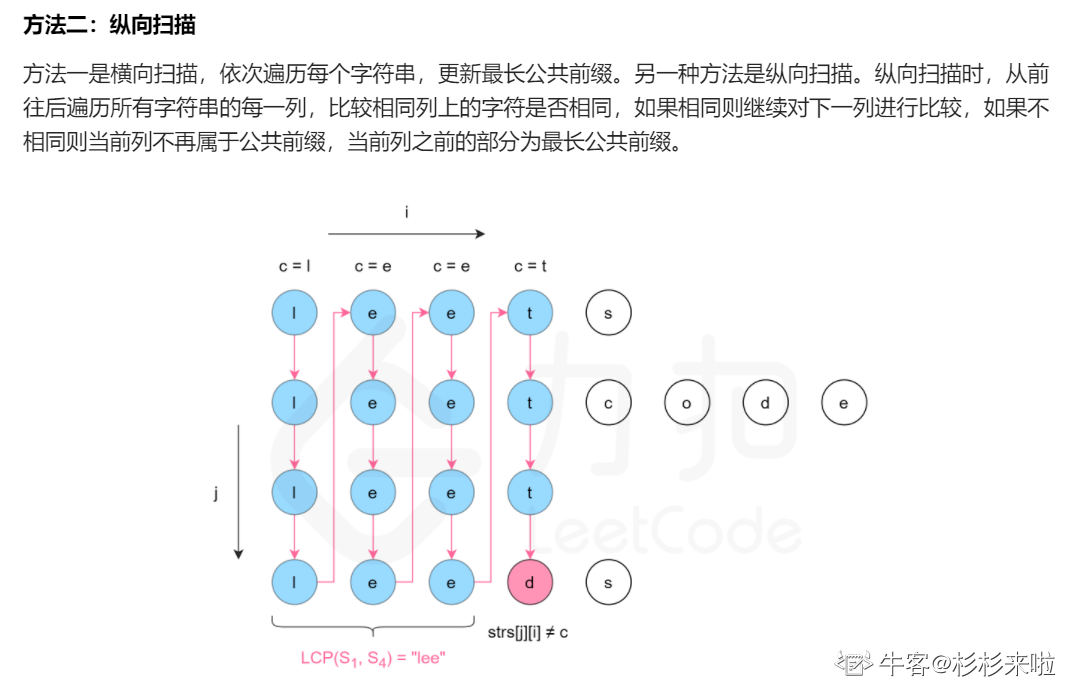
/*by myself(纵向比较)
int i = 0; //对数组中的每个字符串,从第i=0个字符开始比较(纵向比较)
while (1) {
for (auto x : strs) { //遍历每个字符串,将每个字符串的第i个字符与第一个字符串的第i个字符进行比较
if (i == strs[0].size() || i == x.size() || strs[0][i] != x[i]) { //如果不相等或者比较字符下标超出字符串范围,
string str(strs[0], 0, i); //返回第一个字符串前i个字符(这里已经知道前i个字符是最长公共前缀,只需要返回第一个字符的前i个子字符即可)
return str;
}
}
i++; //递增i,比较每个字符串相应的下一个字符
}
*/
/*(横向比较)
if(!strs.size()){
return "";
}
string str = strs[0];
for (int i = 1; i < strs.size(); ++i) {
str = longestCommonPrefix_two(str, strs[i]);
if (!str.size()) {
break;
}
}
return str;
*/
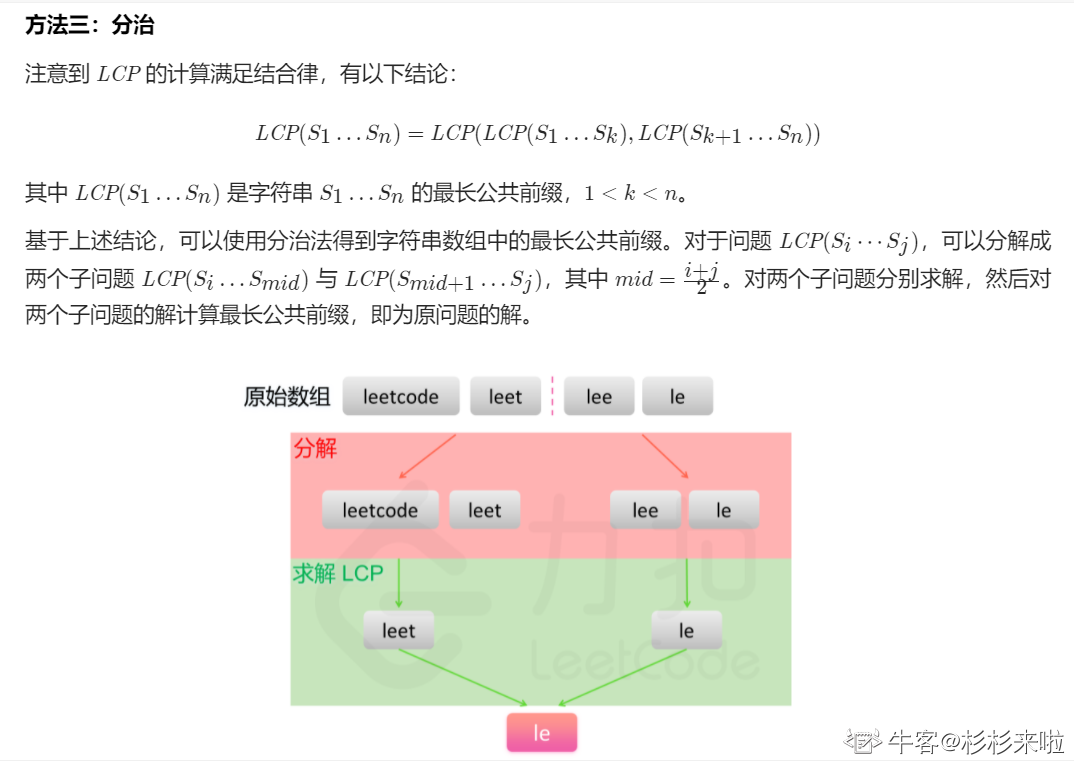
/*(分治)
if (!strs.size()) {
return "";
}
return longestCommonPrefix_fenzhi(strs, 0, strs.size() - 1); //利用分治的思想来得到lcp
*/
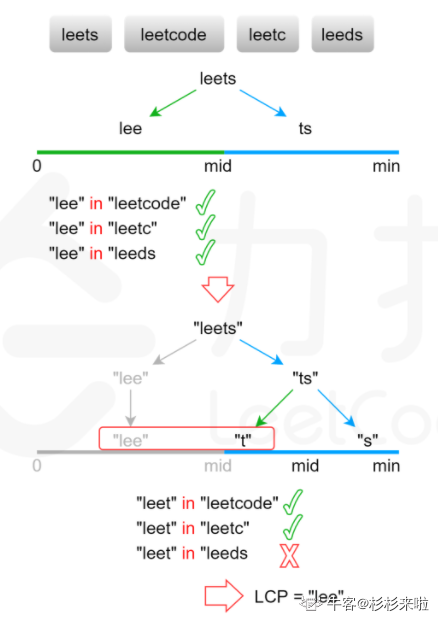
//(二分查找)
if (!strs.size()) {
return "";
}
int minLength = std::min_element(strs.begin(), strs.end(), [](const string& str1, const string& str2) {return str1.size() < str2.size(); })->size(); //利用mid_element函数得到容器中元素的最小值,(注意:这里的目的是为了得到最短字符串的长度,首先利用该函数得到指向该最短字符串的的迭代器。由于元素是字符串不能直接比较,所有要利用第三个参数 定义一个比较器(匿名函数)来进行比较判断。最后再在min_element()后加上->size(),从而取得该最短字符串的长度。(因为lcp一定小于等于最小那个字符串的长度minLength,所以这里取得最小字符串长度,只需从前minLength字符中寻炸,且不用担心溢出)
int low = 0; //开始low设置为0,high为最小字符串的长度
int high = minLength;
while (low < high) { //如果low不小于high表示已经查找结束(low==high),该lcp长度为low或者high
int mid = (high - low + 1) / 2 + low;
if (isCommonPrefix(strs, mid)) {
low = mid;
}
else {
high = mid - 1;
}
}
return strs[0].substr(0, low); //返回第一个字符串的前low个字符
}
};
string Solution::longestCommonPrefix_two(const string& str1, const string& str2) { //返回字符串str1,str2的最长公共前缀
int i = 0;
while (i < str1.size() && i < str2.size()) {
if (str1[i] != str2[i]) {
break;
}
i++;
}
return str1.substr(0, i); //返回从下标0开始长为i的子字符串
}
string Solution::longestCommonPrefix_fenzhi(const vector<string>& strs, int start, int end) { //分治,采用递归分解成(strs/2)组俩俩字符串之间的子问题,俩俩字符串之间得到一个lcp子字符串,再向上合并继续比较,最终得到一个所有字符串的lcp
if (start==end) { //start==end表示已经分解到一个字符串单位,所以lcp就是本身,返回本身即可
return strs[start];
}
int mid = (start + end) / 2; //start!=end表示(start,end)区间还可再分,继续分为新的俩个子区间,即(start,mid)和(mid+1,right)区间
string lcpleft = longestCommonPrefix_fenzhi(strs, start, mid); //lcpleft表示左边区间的lcp
string lcpright = longestCommonPrefix_fenzhi(strs, mid + 1, end); //lcpright表示右边区间的lcp
return longestCommonPrefix_two(lcpleft, lcpright); //最终再计算左右区间lcpleft和lcpright的公共前缀,最终将得到所有字符串的lcp
}
bool Solution::isCommonPrefix(const vector<string>& strs, const int mid) { //判断前mid个字符是否为lcp
for (int i = 1; i < strs.size(); ++i) { //将 第一个字符串的前mid个字符 与之后所有字符串的前mid个字符 进行比较,如果出现不匹配则返回false
for (int j = 0; j < mid; ++j) {
if (strs[0][j] != strs[i][j]) {
return false;
}
}
}
return true;
}
注:
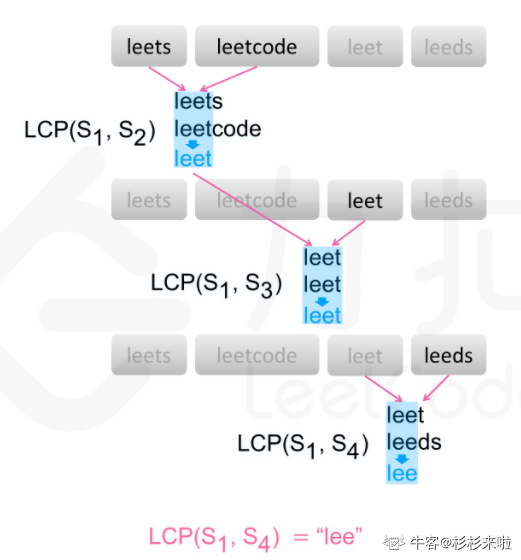







 本文探讨了多个字符串操作问题,如反转字符串、查找子串、最长公共前缀和字符串转整数,通过实例和优化算法展示了如何在有限空间内解决问题,涉及双指针、哈希表和数学技巧的应用。
本文探讨了多个字符串操作问题,如反转字符串、查找子串、最长公共前缀和字符串转整数,通过实例和优化算法展示了如何在有限空间内解决问题,涉及双指针、哈希表和数学技巧的应用。
















 716
716

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








