Abstract
Treiber Stack Algorithm是一个可扩展的无锁栈,利用细粒度的并发原语CAS来实现的,Treiber Stack在 R. Kent Treiber在1986年的论文Systems Programming: Coping with Parallelism中首次出现。
基本原理
该算法的基本原理是:只有当您知道要添加的项目是自开始操作以来唯一添加的项目时,才会添加新的项目。 这是通过使用比较和交换完成的。 在添加新项目时使用堆栈,将堆栈的顶部放在新项目之后。 然后,将这个新构造的头元素(旧头)的第二个项目与当前项目进行比较。 如果两者匹配,那么你可以将旧头换成新头,否则就意味着另一个线程已经向堆栈添加了另一个项目,在这种情况下,你必须再试一次。
当从堆栈中弹出一个项目时,在返回项目之前,您必须检查另一个线程自操作开始以来没有添加其他项目。
正确性
在某些语言中,特别是那些没有垃圾回收的语言,Treiber栈可能面临ABA问题。当一个进程要从堆栈中移除一个元素时(就在下面的pop例程比较和设置之前),另一个进程可以改变堆栈,使得头部是相同的,但是第二个元素是不同的。比较和交换将堆栈的头部设置为堆栈中旧的第二个元素,混合完整的数据结构。但是,由于Java运行时提供了更强大的保证,所以此页面上的Java版本不受此问题的影响(新创建的不混淆的对象引用不可能与任何其他可到达的对象引用相同)。
对诸如ABA之类的故障进行测试可能会非常困难,因为有问题的事件序列非常少见。
Java示例
下面是Java中Treiber Stack的实现,它基于Java Concurrency in Practice提供的
public class ConcurrentStack<E> {
private AtomicReference<Node<E>> top = new AtomicReference<>();
public void push(E item) {
Node<E> newHead = new Node<>(item);
Node<E> oldHead;
do {
oldHead = top.get();
newHead.next = oldHead;
} while (!top.compareAndSet(oldHead, newHead));
}
public E pop() {
Node<E> oldHead;
Node<E> newHead;
do {
oldHead = top.get();
if (oldHead == null)
return null;
newHead = oldHead.next;
} while (!top.compareAndSet(oldHead, newHead));
return oldHead.item;
}
private static class Node<E> {
public final E item;
public Node<E> next;
public Node(E item) {
this.item = item;
}
}
}流程分析
PUSH操作
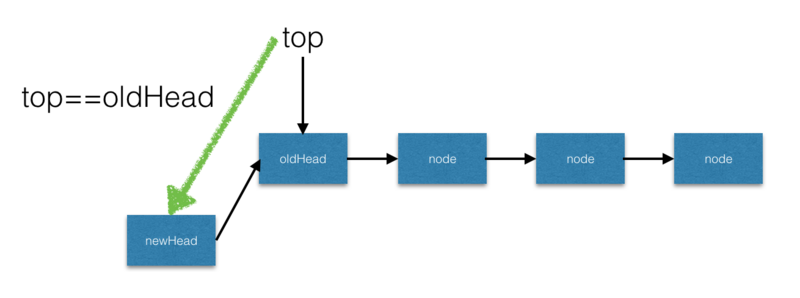
根据上述的描述做图如上,并分析其工作流程。
- 首先单链表保存了各个Stack中的各个元素,成员变量top持有了栈的栈顶元素。
- 当执行push操作时,首先创建一个新的元素为
newHead,并让该新节点的next指针指向top节点(此时top=oldHead)。 - 最后通过CAS替换
top=newHead,CAS的交换条件是top=oldHead。 - 当条件满足后,操作后的状态如下:
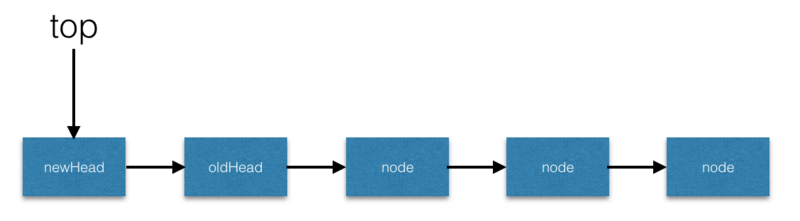
POP操作

根据上述的描述做图如上,并分析其工作流程。
- 当执行pop操作时,创建一个新的指针,该指针指向
top的next元素。 - 然后通过CAS替换
top=newHead,CAS的交换条件是top=oldHead。 - 当条件满足后,操作后的状态如下:

























 293
293

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








