20190815 t2

t2题目

洛谷 P5428

跨栏
(jump.cpp/c/pas)
【问题描述】
在过去，校长曾经构思了许多新式学生运动项目的点子，其中就包括学生障碍赛，是学生们在赛道上跑越障碍栏架的竞速项目。他之前对推广这项运动做出的努力结果喜忧参半，所以他希望在他的操场上建造一个更大的学生障碍赛的场地，试着让这项运动更加普及。校长为新场地精心设计了N个障碍栏架，编号为1…N（2≤N≤105），每一个栏架都可以用这一场地的二维地图中的一条线段来表示。这些线段本应两两不相交，包括端点位置。
不幸的是，校长在绘制场地地图的时候不够仔细，现在发现线段之间出现了交点。然而，他同时注意到只要移除一条线段，这张地图就可以恢复到预期没有相交线段的状态（包括端点位置）。
请求出校长为了恢复没有线段相交这一属性所需要从他的计划中删去的一条线段。如果有多条线段移除后均可满足条件，请输出在输入中出现最早的线段的序号。
【输入格式】
输入的第一行包含N。余下N行每行用四个整数x1 y1 x2 y2表示一条线段，均为至多109的非负整数。这条线段的端点为(x1,y1)和(x2,y2)
。所有线段的端点各不相同。
【输出格式】
输出在输入中出现最早的移除之后可以使得余下线段各不相交的线段序号。
【输入样例】
4
2 1 6 1
4 0 1 5
5 6 5 5
2 7 1 3
【输出样例】
2

赛况

这道题呢，特别的难，因为要判断相交，但自己不会解析几何，于是就打的斜率算交点，再判断是否在两条线段上，……，好像特别的捞，0分直接到手，再一次WA穿

场上有为jvlao freopen 直接把这道题A了，tql，orz。

也有人花式爆搜，直达90分，tql，orz

铺垫

判断两条线段是否相交，可以使用对立叉乘试验。
首先介绍一下叉乘。

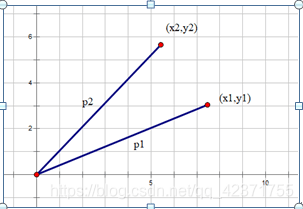
如上图所示：p1和p2是两条线段，它们的一个端点在原点(0,0)，p1的另一个端点在(x1,y1)处,p2的另一个端点在(x2,y2)处。
线段p1与p2的叉乘为：p1×p2=(x1y2)-(x2y1)
如果叉乘大于0，表示p2在p1的顺时针180度以内，如果小于0，表示p2在p1的逆时针180度以内，如果等于0，表示p1和p2重合。
现在要判断两条线段是否交叉，我们可以取线段1的一个端点，和另一条线段的两个端点各组成一条线段，如下图的虚线：

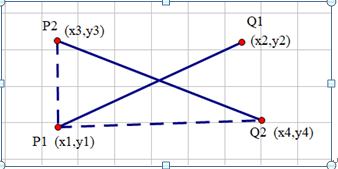
取(x1,y1)和(x3,y3)构成一条虚线，取（x1,y1）和(x4,y4)构成一条虚线，设线段<P1,Q2>与<P1,Q1>的叉乘为m1，线段<P1,Q1>与线段<P1,P2>的叉乘为m2，如果m1*m2>=0,则说明Q2和P2在线段<P1,Q1>的两侧或在线段上面。

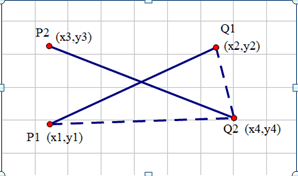
然后再取(x4,y4)和(x1,y1)构成一条虚线，取(x4,y4)和(x2,y2)构成一条虚线，设线段<Q2,P1>与线段<Q2,P2>的叉乘为n1，线段<Q2,P2>与<Q2,Q1>的叉乘为n2，如果n1*n2>=0,则说明P1和Q1分别在线段<P2,Q2>的两侧或在线段上面。
这样就能判断出来线段<P1,Q1>与线段<P2,Q2>是否相交了。

正解

常规做法：二重循环直接判断那两条线段相交，再从两条线段中判断是否有其他线段与之相交，若有则输出此答案，若两条线段都没有，则输出先出现的线段。

看起来好像是没有什么问题，看一下时间复杂度，O（n^2），T了。

据说正解是要用扫描线+set优化到 O（nlog(n)），行的通了，可是感觉代码实现非常的难，不会。

在这道题当中，要求最高的便是求出两条相交的线段，只要快速的求出，胜利就在向你招手。

最初，我们要把每个点排序：按照x由小到大排序，x相同的按照y由小到大排序。

然后扫描线走起，若为左端点，直接将这条线段压进去，在判断它与前后两条线有没有相交，若有直接break，不然继续去扫描。

有人会问：为什么只用判断前后两条线呢
摘自题解：Set中的线段则按照当前扫描的x坐标对应的y值排序。因为set中的线段一定是跨越当前这个x位置的，如果没有相交，则他们的y坐标的顺序不会发生变化。

代码（题解给的，作者还在研究中）

#include <iostream>
#include <fstream>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
typedef long long LL;

int N;
double x;
struct Point { LL x, y; int segindex; };
struct Segment { Point p, q; int index; };

bool operator< (Point p1, Point p2) { return p1.x==p2.x ? p1.y<p2.y : p1.x<p2.x; }

// Intersection testing (here, using a standard "cross product" trick)
int sign(LL x) { if (x==0) return 0; else return x<0 ? -1 : +1; }
int operator* (Point p1, Point p2) { return sign(p1.x * p2.y - p1.y * p2.x); }
Point operator- (Point p1, Point p2) { Point p = {p1.x-p2.x, p1.y-p2.y}; return p; }
bool isect(Segment &s1, Segment &s2)
{
  Point &p1 = s1.p, &q1 = s1.q, &p2 = s2.p, &q2 = s2.q;
  return ((q2-p1)*(q1-p1)) * ((q1-p1)*(p2-p1)) >= 0 && ((q1-p2)*(q2-p2)) * ((q2-p2)*(p1-p2)) >= 0;
}

// What is the y coordinate of segment s when evaluated at x?
double eval(Segment s) {
  if (s.p.x == s.q.x) return s.p.y;
  return s.p.y + (s.q.y-s.p.y) * (x-s.p.x) / (s.q.x-s.p.x);
}
bool operator< (Segment s1, Segment s2) { return s1.index != s2.index && eval(s1)<eval(s2); }
bool operator== (Segment s1, Segment s2) { return s1.index == s2.index; }

int main(void)
{
  ifstream fin ("jump.in");
  vector<Segment> S;
  vector<Point> P;

  fin >> N;
  for (int i=0; i<N; i++) {
    Segment s;
    fin >> s.p.x >> s.p.y >> s.q.x >> s.q.y;
    s.index = s.p.segindex = s.q.segindex = i;
    S.push_back(s);
    P.push_back(s.p); P.push_back(s.q);
  }
  sort (P.begin(), P.end());

  set<Segment> active;
  int ans1, ans2; // sweep across scene to locate just one intersecting pair...
  for (int i=0; i<N*2; i++) {
    ans1 = P[i].segindex; x = P[i].x;
    auto it = active.find(S[ans1]);
    if (it != active.end()) {
      // segment already there -- we've reached its final endpoint.  check intersection with the
      // pair of segments that becomes adjacent when this one is deleted.
      auto after = it, before = it; after++;
      if (before != active.begin() && after != active.end()) {
	before--;
	if (isect(S[before->index], S[after->index]))
	  { ans1 = before->index; ans2 = after->index; break; }
      }
      active.erase(it);
    }
    else {
      // new segment to add to active set.
      // check for intersections with only the segments directly above and below (if any)
      auto it = active.lower_bound(S[ans1]);
      if (it != active.end() && isect(S[it->index], S[ans1])) { ans2 = it->index; break; }
      if (it != active.begin()) { it--; if (isect(S[it->index], S[ans1])) { ans2 = it->index; break; } }
      active.insert(S[ans1]);
    }
  }

  if (ans1 > ans2) swap (ans1, ans2);
  int ans2_count = 0;
  for (int i=0; i<N; i++)
    if (S[i].index != ans2 && isect(S[i], S[ans2])) ans2_count++;

  ofstream fout ("jump.out");
  fout << (ans2_count > 1 ? ans2+1 : ans1+1) << "\n";
  return 0;
}