最短路算法

1-floyd

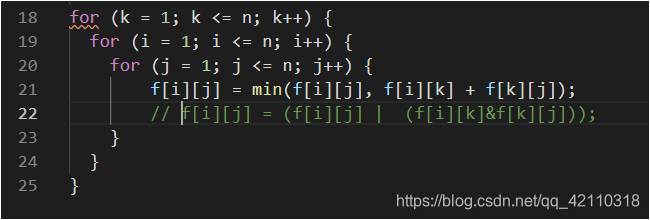
floyed传递闭包
判断图中两点之间是否可达

for(int k=1;k<=n;k++)
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			f[i][j]|=f[i][k]&f[k][j];

for(int k=1;k<=n;k++)
	for(int i=1;i<=n;i++)if(f[i][k])
		for(int j=1;j<=n;j++)if(f[k][j])
			f[i][j]=true;

拓展

& 当然spfa也可以单源最短路的最短路数量

2-dijkstra

1. 范围：正权边，复杂度(n+m)logn
   https://www.luogu.org/problemnew/show/P3371

int dis[N];
bool vis[N];//两个集合{s,t}
priority_queue <pair<int,int> > q;// t集合里，到s任意一点的距离的点（按距离近远排序）
void dijkstra(int s)
{
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));// 有没有被放进s集合里
	dis[s]=0;
	q.push(make_pair(0,s));
	while(!q.empty())
	{
		int u=q.top().second;q.pop();
		if(vis[u]) continue;
		vis[u]=true;//用过他之后就把他放进s里
		for(int i=head[u];i;i=edge[i].nxt)
		{
			int v=edge[i].v;
			int w=edge[i].w;
			if(dis[u]+w<dis[v])
			{
				dis[v]=dis[u]+w;
				q.push(make_pair(-dis[v],v));//更新每个点的远近，用于找下一个离s最近的点
			}
		}
	}
}

3-SPFA

范围：单源最短路，可以做有负权边的图
复杂度：O（km）注意这个K可大可小

https://www.luogu.org/problemnew/show/P3371

queue <int> q;
int dis[N];
bool vis[N];
void spfa(int s)
{
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	q.push(s);
	dis[s]=0;
	vis[s]=true;//表示s在可更新别的点的队列中
	while(!q.empty())//队列不为空
	{
		int u=q.front();
		q.pop();
		vis[u]=false;//不在队列
		for(int i=head[u];i;i=edge[i].nxt)
		{
			int v=edge[i].v;
			int w=edge[i].w;
			if(dis[u]+w<dis[v])
			{
				dis[v]=dis[u]+w;
				if(!vis[v])//如果不在队列
				{
					q.push(v);//就放进队列
					vis[v]=true;
				}
			}
		}
	}
}

拓展
spfa可以判负环，只需要在q.push(v)这个地方记录一下v被push了多少次就可以了，如果push了n次，就出现了负环

优化

https://www.cnblogs.com/bljfy/p/9262309.html
具体的有SLF和LLL优化
SLF优化15%~20%：
if(dis[v]<dis[u]) push_front
else push_back

SLF+LLL优化50%

优化过后的代码

deque <int> q;
int dis[N];
bool vis[N];
void spfa(int s)
{
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	q.push_front(s);
	dis[s]=0;
	vis[s]=true;//表示s在可更新别的点的队列中
	while(!q.empty())//队列不为空
	{
		int u=q.front();
		q.pop_front	();
		vis[u]=false;//不在队列
		for(int i=head[u];i;i=edge[i].nxt)
		{
			int v=edge[i].v;
			int w=edge[i].w;
			if(dis[u]+w<dis[v])
			{
				dis[v]=dis[u]+w;
				if(!vis[v])//如果不在队列
				{
					if(dis[v]<dis[q.front()] q.push_front(v);
					else q.push_back(v);
					//就放进队列
					vis[v]=true;
				}
			}
		}
	}
}