算法思路:
①辗转相除法
将两个数a,b相除,如果余数c不等于0,就把b的值给a,c的值给b,直到c等于0,此时最大公约数就是b。
②更相减损术
将两个数中较大的数a减去较小的数b,如果差c等于0,那么最大公约数为b,如果不等于0,则将b的值给a,c的值给b,继续相减直到差等于0。
③穷举法
将两个数a,b中较小的值赋给i,将a除以i,b也除以i,若两者的余数同时为0时,此时的i就是两者的最大公约数。
代码如下:
public class Court {
static int temp;
public static void main(String[] args) {
// TODO Auto-generated method stub
Court c = new Court();
c.Division(23, 45);
c.Substrct(45, 12);
c.Exhaus(88, 34);
/*
* MyThread mythread = new MyThread(); Thread thread = new
* Thread(mythread); thread.start();
*/
}
// 辗转相除法实现
int Division(int a, int b) {
// int temp = 0;
if (a < b) {
temp = a;
a = b;
b = temp;
}
if ((a % b) != 0) {
temp = a % b;
a = b;
b = temp;
return Division(a, b);
}
System.out.println("a和b的最大公约数是:" + b);
// return Division(a, b);
return 0;
}
// 相减法实现
int Substrct(int a, int b) {
// int temp = 0;
if (a < b) {
temp = a;
a = b;
b = temp;
}
if ((a - b) != 0) {
temp = a - b;
a = b;
b = temp;
// return a;
return Substrct(a, b);
}
System.out.println("a和b的最大公约数是:" + b);
// return Substrct(a, b);
return 0;
}
// 穷举法实现
int Exhaus(int a, int b) {
if (a == b) {
System.out.println("a和b的最大公约数是:" + a);
return a;
}
if (a > b) {
temp = b;
} else {
temp = a;
}
while ((a % temp) != 0 || (b % temp) != 0) {
temp--;
}
System.out.println("a和b的最大公约数是:" + temp);
return 0;
}
}
测试数据:23,45;45,12,;88,34;
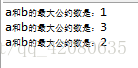
测试结果:






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








