1、树的基本概念
树结构是一类重要的非线性数据结构,树中结点之间具有明确的层次关系,并且结点之间具有分支,类似于正真的树。
在图形表示的树型结构中,对两个用线段(树枝)连接的相关联的结点,称上端结点为下端结点的父节点,称下端结点为上端结点的子结点。对同一个父结点的多个子结点互称兄弟结点,对从根结点到某个子结点所经过的所有结点称为这个子结点的祖先,对以某个结点为根的子树中的任一结点都是该结点的子孙。
对于树中任意两个不同的结点,如果从一个结点出发,自上而下沿着树中连着结点的线段能到达另一结点,则称它们之间存在着一条路径。可用路径所经过的结点序列表示路径,其长度等于路径上的结点个数减1。从根节点出发,到树中的其余结点一定存在着一条路径,不同子树上的结点之间不存在路径。
由于一条边连接两个结点,且树中不存在环,因此对有n个结点的树,边数一定是n-1 但满足连通、边数等于顶点数-1的结构一定是一棵树。
结点的度:一个结点拥有的子数树称为该结点的度。
树的度:一棵树中结点的最大度数定义为该树的度。
叶结点(或终端结点):度数为0的结点称为叶结点。
结点的层数:从根算起,设根的层数为1,其余结点的层数次等于其双亲结点的层数加一。
树的深度:树中结点的最大层数称为树的深度(或高度)。
森林:多棵树组合在一起称为森林,即森林是若干树的集合。
数的示意图
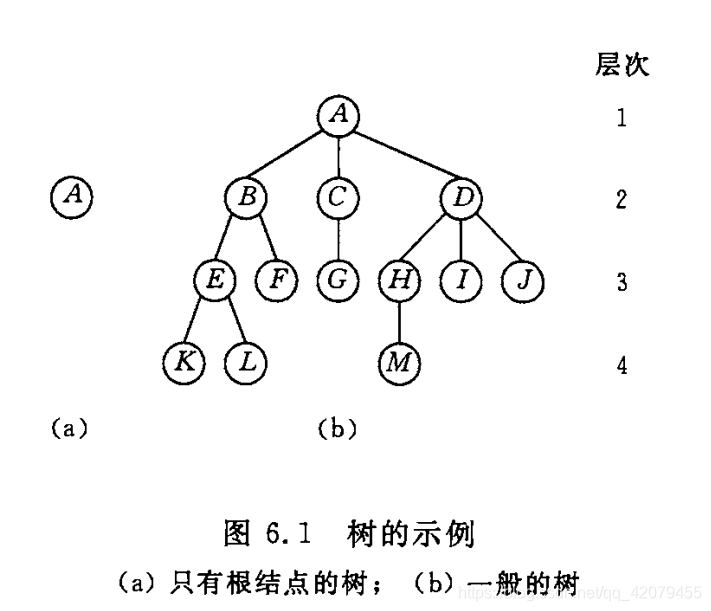
2、二叉树概述
定义:
二叉树是另一种树型结构,它的特点是每个结点至多只有两颗子树(即二叉树中不存在度大于二的结点)并且二叉树子树有左右之分,其顺序不能任意颠倒。
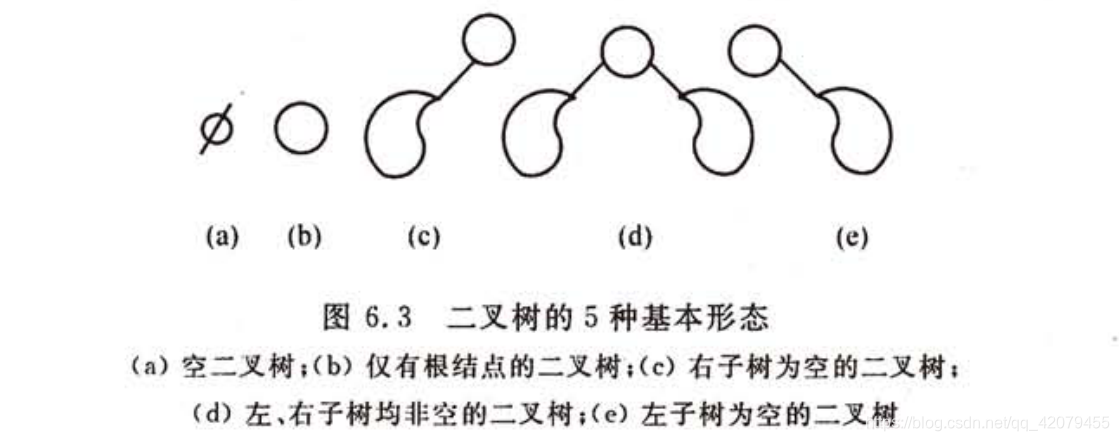
2.1二叉树的性质
(1)二叉树的第i层上的结点树最多为2^(i-1)其中(i>=1)
(2)深度为k的二叉树至多有2^k-1个结点
(3)对任何一棵二叉树,如果叶子结点树为n0,度为2的结点树为n2,则就有:n0=n2+1
(4) 具有n个结点的完全二叉树的深度为[log2为底n]+1([x]表示小于x的最大整数 )
对于(3)这个性质的证明:
设度为0的结点个数为n0, 设度为1的结点个数为n1, 设度为0的结点个数为n2, 结点的总数为n
得到: n=n0+n1+n2----------------(1)
又因为除了根结点为,其余结点都有一个分支进入,所以就有 结点总数=分支数+1,又因为度为1的
结点有一个分支指出,度为2的结点有两个分支指出
得到: n=n1+2*n2+1---------------(2)
(2)-(1)得到:n0=n2+1
2.2二叉树的两种特殊情形
(1)满二叉树: 每一层的结点个数都达到了当层能达到的最大结点数,(或:一棵深度为k且有2^k-1个结点二叉树)
(2)完全二叉树: 一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树。
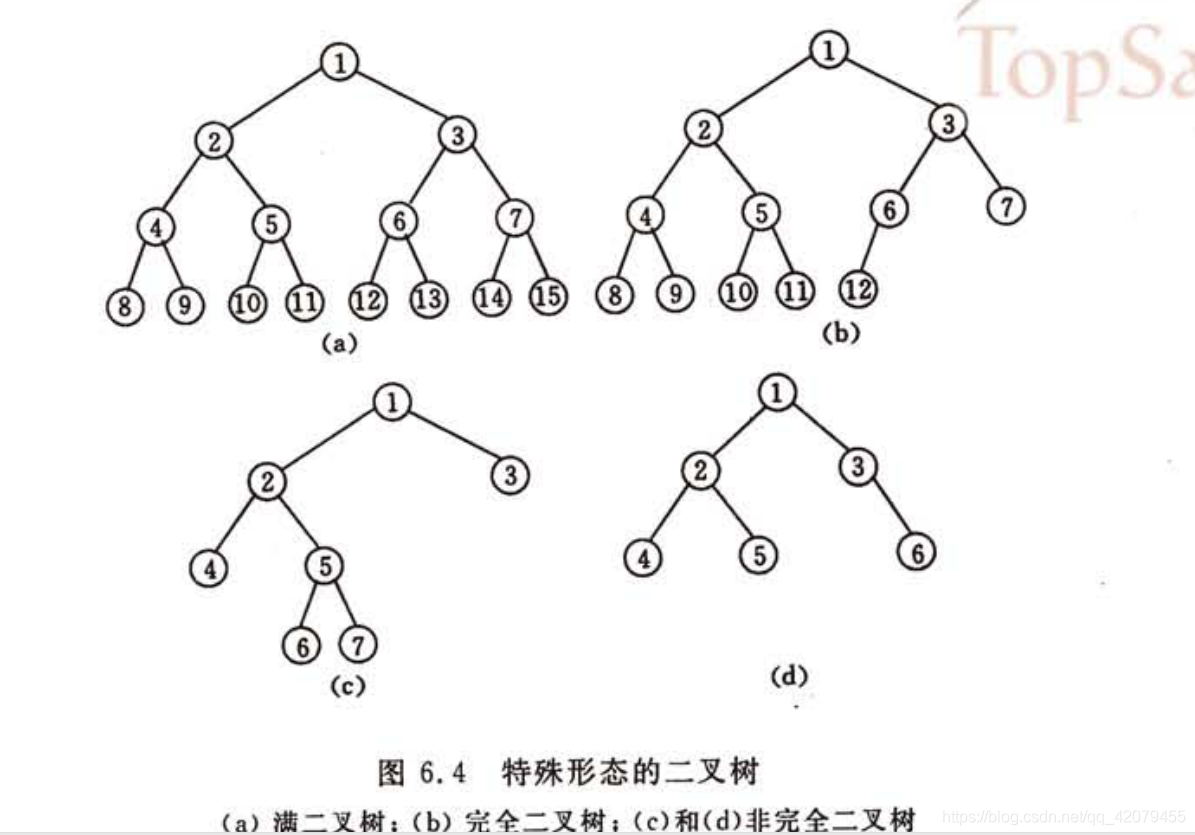
2.3二叉树的存储
(1)顺序存储:顺序存储一棵二叉树时,首先要对该树的每个结点进行编号,然后以个结点的编号为 i下标,把各结点的值对应存储到一维数组[i-1]中。树中结点的编号与等深度的完全二叉树中对应位置上结点的编号相同
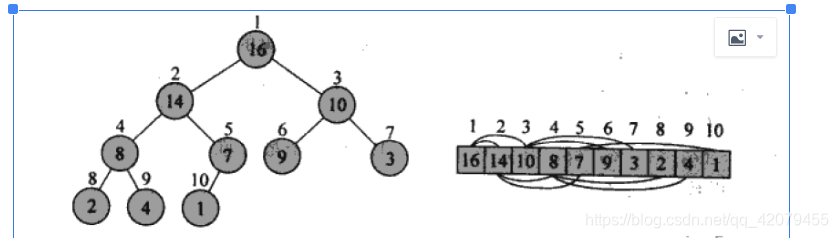
import java.util.Arrays;
public class BTree<T> {
// 使用数组来存储所有的结点
private Object[] datas;
// 默认的树深度
private final int DEFAULT_DEEP = 10;
// 树的深度
private int deep;
// 数组的长度
private int length=0;
private int size;
// 以默认的深度创建二叉树
public BTree() {
this.deep = DEFAULT_DEEP;
// 深度为k的二叉树至多有2^k-1个结点
this.size = (int) Math.pow(2, deep)-1;
datas = new Object[size];
}
// 以指定的深度创建二叉树
public BTree(int deep) {
this.deep = deep;
this.size = (int) Math.pow(2, deep)-1;
datas = new Object[size];
}
// 以指定深度,指定结点创建二叉树
public BTree(int deep, T data) {
this.deep = deep;
this.size = (int) Math.pow(2, deep)-1;
datas = new Object[size];
datas[0] = data;
length++;
}
/*
* 为指定的结点添加子结点
* pIndex 需要添加子结点的父结点索引
* data 新子结点的数据
* left 新子结点是否为左结点
*/
public void add(int pIndex, T data, boolean left) {
// 先判断其父结点是否为空
if (datas[pIndex-1] == null) {
throw new RuntimeException(pIndex + "处结点为空,无需添加子结点!");
}
//左儿子的结点索引为2 * pIndex,右儿子的结点索引为2 * pIndex+1
if (2 * pIndex > size || 2 * pIndex + 1 > size) {
throw new RuntimeException("树底层数组已满");
}
if (left) {
if (datas[2 * pIndex - 1] == null) {
datas[2 * pIndex - 1] = data;
} else {
throw new RuntimeException("该节点已存在!");
}
} else {
if (datas[2 * pIndex] == null) {
datas[2 * pIndex] = data;
} else {
throw new RuntimeException("该节点已存在!");
}
}
length++;
}
public boolean isEmpty() {
return datas[0] == null;
}
// 获取父结点
public T getPNode(int index) {
checkIndex(index);
if (index == 1)
throw new RuntimeException("根节点不存在父节点!");
if(datas[index-1]==null)
throw new RuntimeException("该节点不存在父节点!");
return (T) datas[(index) / 2-1];
}
// 获取右子结点
public T getRight(int index) {
checkIndex((index) * 2+1);
return (T) datas[index * 2 ];
}
// 获取左子结点
public T getLeft(int index) {
checkIndex(index * 2);
return (T) datas[index * 2-1];
}
// 返回该二叉树的深度
public int getDeep() {
return deep;
}
// 返回指定数据的位置
public int indexOf(T data) {
if (data == null) {
// 不能为空
throw new NullPointerException();
} else {
for (int i = 0; i < datas.length; i++) {
if (data.equals(datas[i])) {
return i+1;
}
}
}
return -1;
}
// 总共有多少个结点
public int getLength() {
return length;
}
//判断下标是否越界
public void checkIndex(int index) {
if (index < 0 || index > datas.length)
throw new IndexOutOfBoundsException();
}
public String toString() {
return Arrays.toString(datas);
}
}
(2)链式存储:在二叉树的链式存储中,通常采用的方法是在每个结点中设置三个域,即值域、左指针域、右指针域。有时候为了便于找到一个结点的双亲,也可以增加一个指向其双亲的指针域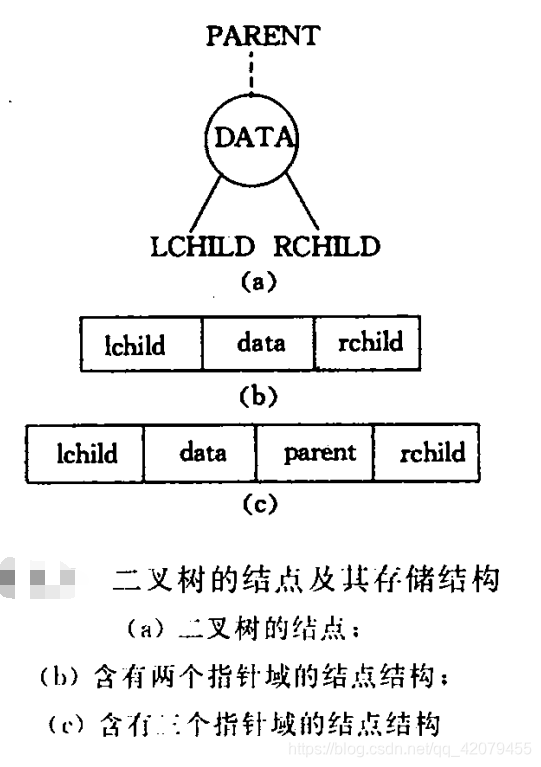
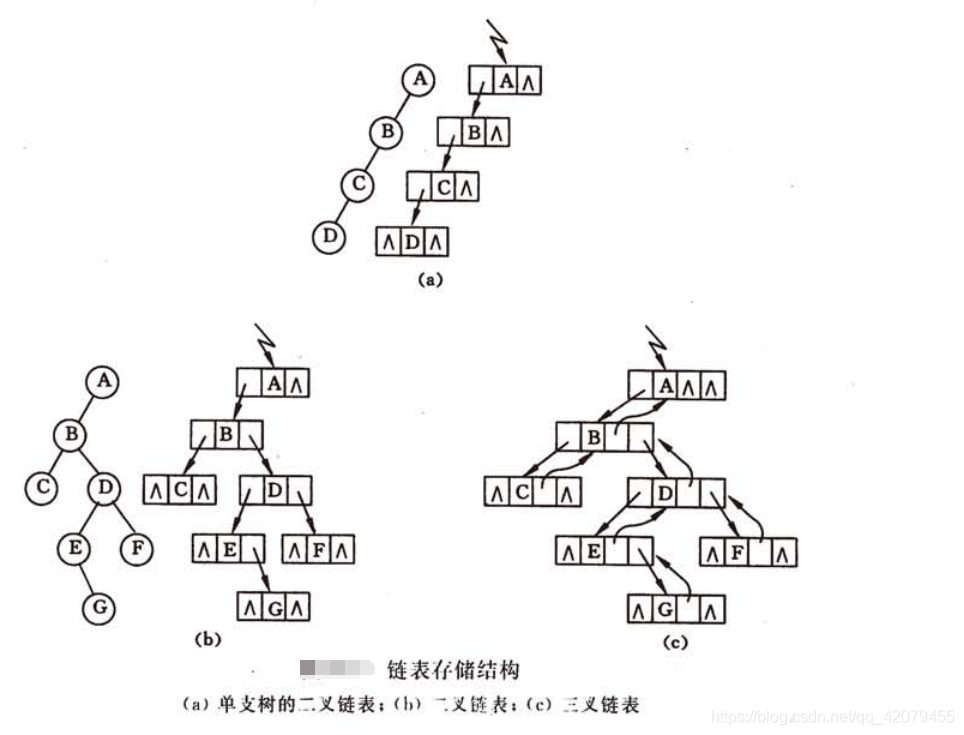
java代码:
public class TwoLinkBinTree<T> {
/*
* 使用java实现二叉树的二叉链表存储
* 注意:因为二叉树不是线性结构,当使用顺序存储(数组)时和其他线性结构的操作差别不是很大,
* 但是如果使用二叉链表来存储时,则差别很大!具体的差别见如下代码实现。
* 要求:
* 1.定义一个私有的内部类,用来存储节点信息
* 2.定义一个私有的节点变量,用来指向根节点
* 3.提供诺干方法用来操作二叉树
* */
public static class Node{
Object data;
Node left;
Node right;
public Node(){
}
public Node(Object data){
this.data=data;
this.left=null;
this.right=null;
}
public Node(Object data,Node left,Node right){
this.data=data;
this.left=left;
this.right=right;
}
}
private Node root;
//默认的无参构造函数
public TwoLinkBinTree(){
root = new Node();
}
//根据提供的元素构造二叉树
public TwoLinkBinTree(T data){
root = new Node(data);
}
//为指定节点添加子节点
public Node add(Node parent,T data,boolean isLeft){
//如果提供的节点为空,则不能添加子节点
if(parent==null||parent.data==null){
throw new RuntimeException("节点为空的不能添加子节点");
}
Node node=null;
if(isLeft){//如果要添加的是左子节点
if(parent.left!=null){
throw new RuntimeException("该节点的左子节点已经存在");
}else{
node=new Node(data);
parent.left=node;
}
}else{//否则添加的是右子节点
if(parent.right!=null){
throw new RuntimeException("该节点的右子节点已经存在");
}else{
node=new Node(data);
parent.right=node;
}
}
return node;
}
//判断二叉树是否为空
public boolean isEmpty(){
//这里之所以是对data进行判断是因为提供的构造函数都能够保证root不为空,但是data有可能为空
return root.data==null;
}
//获取根节点
public Node getRoot(){
if(isEmpty()){
throw new RuntimeException("树为空,不能获取根节点");
}
return root;
}
//如果使用的是无参的二叉树构造函数,则可以调用这个方法为root的data设置值
public void setRootData(T data){
if(root!=null&&root.data==null){
root.data=data;
}else{
throw new RuntimeException("该根节点已经有数据,不能重新设置");
}
}
//获取指定节点的左子节点
public Node getLeft(Node parent){
if(parent==null){
throw new RuntimeException("该根节点为空没有左子节点");
}else{
return parent.left;
}
}
//获取指定节点的右子节点
public Node getRight(Node parent){
if(parent==null){
throw new RuntimeException("该根节点为空没有右子节点");
}else{
return parent.right;
}
}
//获取二叉树的深度
public int getDeep(){
return deep(root);
}
//获取指定节点之下的深度
private int deep(Node node){
if(node==null){
return 0;
}
if(node.left==null&&node.right==null){
return 1;
}else{//采用递归的算法,遍历整个二叉树,每次将节点的最大深度(左子树、右子树深度不一致)传递给父节点
int leftDeep=deep(node.left);
int rightDeep=deep(node.right);
//去深度最大值
int max=leftDeep>rightDeep?leftDeep:rightDeep;
return max+1;
}
}
}
3、二叉树的运算
3.1二叉树的遍历
二叉树的定义是递归的,一棵非空的二叉树是由根节点、左子树、右子树3个基本部分组成的,因此遍历一棵非空的二叉树的问题可分解为3个子问题:访问根节点、遍历左子树和遍历右子树。
遍历分为3种:
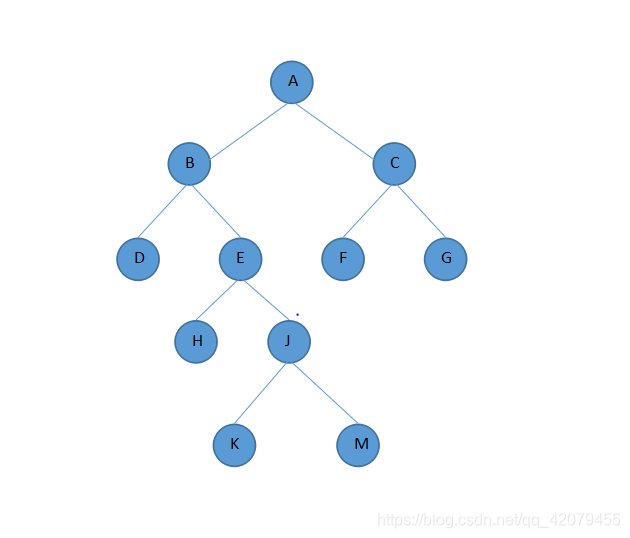
(1)前序遍历二叉树: A B D E H J K M C F G
(2)中序遍历二叉树: D B H E K J M A F C G
(3)后续遍历二叉树: D H K M J E B F G C A
树的三种遍历方式的递归和非递归实现,在下篇博客上详细讲述。敬请期待,吼吼吼!




















 2315
2315

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








