二叉堆

完全二叉树

完全二叉树：对于一个树高为h的二叉树，如果其第0层至第h-1层的节点都满。如果最下面一层节点不满，则所有的节点在左边的连续排列，空位都在右边。这样的二叉树就是一棵完全二叉树。

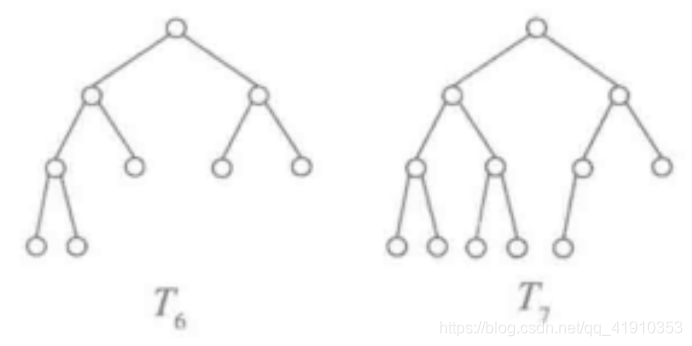
完全二叉树的性质
如果一棵具有n个结点的深度为k的二叉树，它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应，这棵二叉树称为完全二叉树。
可以根据公式进行推导，假设n0是度为0的结点总数（即叶子结点数），n1是度为1的结点总数，n2是度为2的结点总数，则 ：
①n= n0+n1+n2 （其中n为完全二叉树的结点总数）；又因为一个度为2的结点会有2个子结点，一个度为1的结点会有1个子结点，除根结点外其他结点都有父结点，
②n= 1+n1+2n2 ；由①、②两式把n2消去得：n= 2n0+n1-1，由于完全二叉树中度为1的结点数只有两种可能0或1，由此得到n0=n/2 或 n0=(n+1)/2。
简便来算，就是 n0=n/2，其中n为奇数时（n1=0）向上取整；n为偶数时（n1=1）。可根据完全二叉树的结点总数计算出叶子结点数。
ALDS1_9_A:完全二叉树代码实现

#include<bits/stdc++.h>
using namespace std;
#define MAX 100000
int parent(int i) {
 return i/2;
}
int left(int i) {
 return i*2;
}
int right(int i) {
 return 2*i+1;
}
int main() {
 int h,i,a[MAX+1];
 cin>>h;
 for(i=1; i<=h; i++)cin>>a[i];
 for(i=1; i<=h; i++) {
  cout << "node " << i << ": key = " << a[i] << ", ";
  if(parent(i)>=1)cout << "parent key = " << a[parent(i)] << ", ";
  if(left(i)<=h)cout << "left key = " << a[left(i)] << ", ";
  if(right(i)<=h)cout << "right key = " << a[right(i)] << ", ";
  cout<<endl;
 }
 return 0;
}

堆

堆通常是一个可以被看做一棵树，它满足下列性质：
性质一] 堆中任意节点的值总是不大于(不小于)其子节点的值；
[性质二] 堆总是一棵完全树。
将任意节点不大于其子节点的堆叫做最小堆或小根堆，而将任意节点不小于其子节点的堆叫做最大堆或大根堆。常见的堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等等。

二叉堆

二叉堆是完全二元树或者是近似完全二元树，它分为两种：最大堆和最小堆。
最大堆：父结点的键值总是大于或等于任何一个子节点的键值；最小堆：父结点的键值总是小于或等于任何一个子节点的键值。示意图如下：

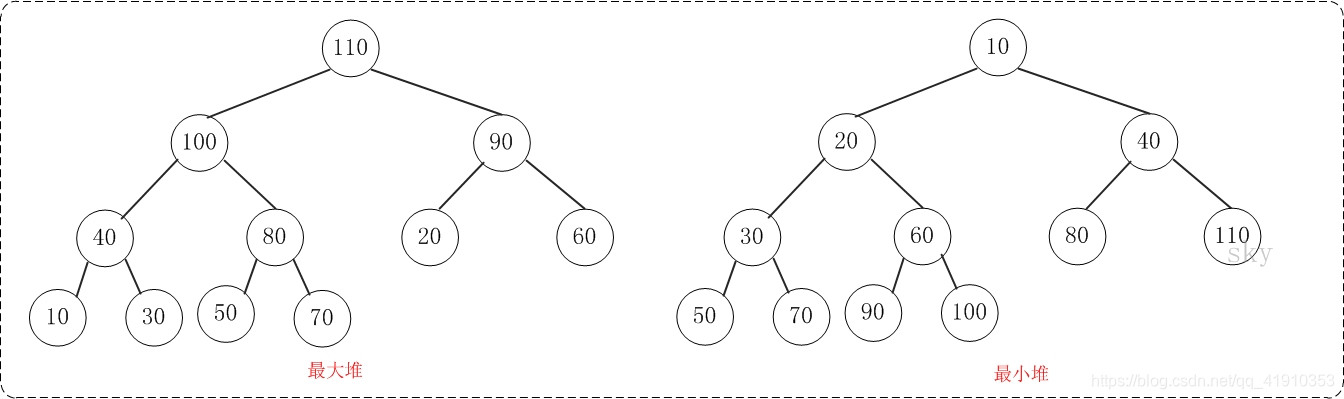
二叉堆一般都通过"数组"来实现。数组实现的二叉堆，父节点和子节点的位置存在一定的关系。有时候，我们将"二叉堆的第一个元素"放在数组索引0的位置，有时候放在1的位置。当然，它们的本质一样(都是二叉堆)。
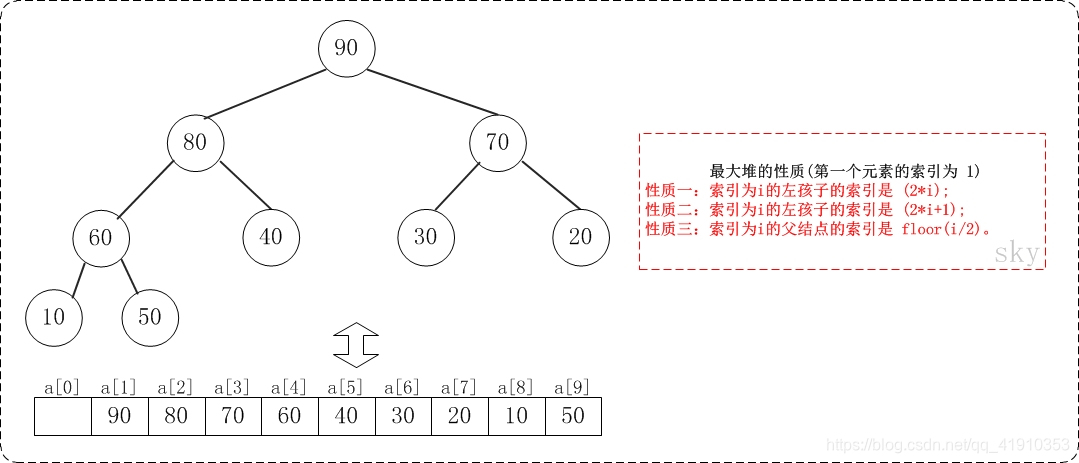
假设"第一个元素"在数组中的索引为 1 的话，则父节点和子节点的位置关系如下：
(01) 索引为i的左孩子的索引是 (2i);
(02) 索引为i的左孩子的索引是 (2i+1);
(03) 索引为i的父结点的索引是 floor(i/2);

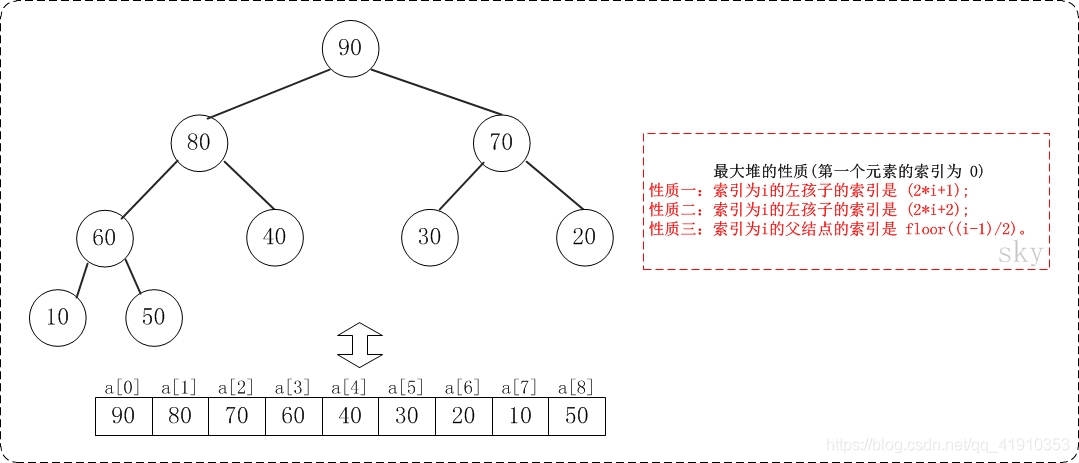
如果假设"第一个元素"在数组中的索引为 0 的话，则父节点和子节点的位置关系如下：
(01) 索引为i的左孩子的索引是 (2i+1);
(02) 索引为i的左孩子的索引是 (2i+2);
(03) 索引为i的父结点的索引是 floor((i-1)/2);

第一个元素以 1 为索引

#include<bits/stdc++.h>
using namespace std;
#define MAX 600000
int h,a[MAX+1];
void maxheapify(int i) {
 int l,r,largest;
 l=2*i;
 r=2*i+1;
 if(l<=h&&a[l]>a[i]) largest=l;
 else largest=i;
 if(r<=h&&a[r]>a[largest]) largest=r;
 if(largest!=i) {
  swap(a[i],a[largest]);
  maxheapify(largest);
 }
}
int main() {
 cin>>h;
 for(int i=1; i<=h; i++)cin>>a[i];
 for(int i=h/2; i>=1; i--) maxheapify(i);
 for(int i=1; i<=h; i++) {
   cout<<" "<<a[i];
 }
 cout<<endl;
 return 0;
}

优先级队列

最小堆实现演示

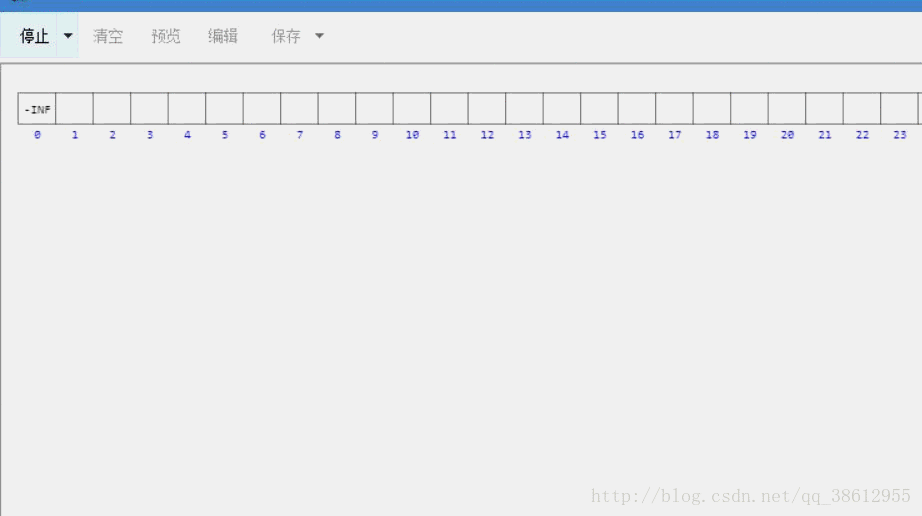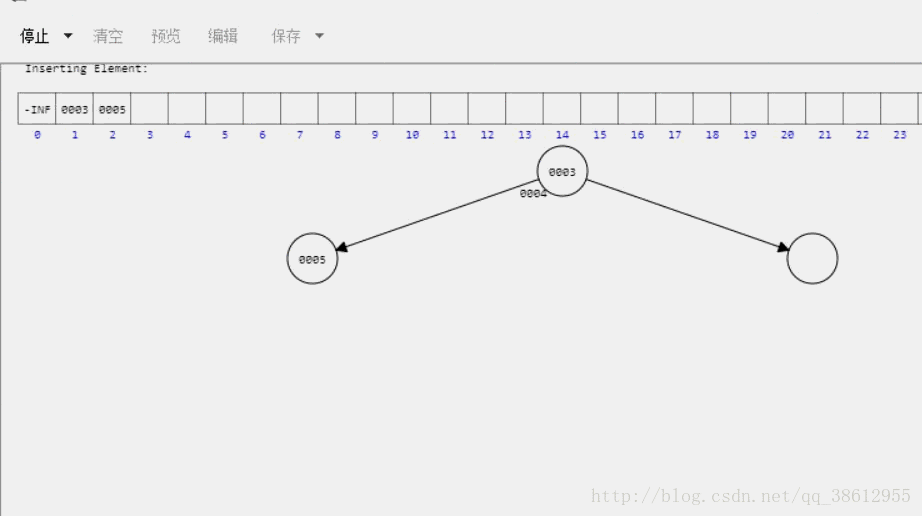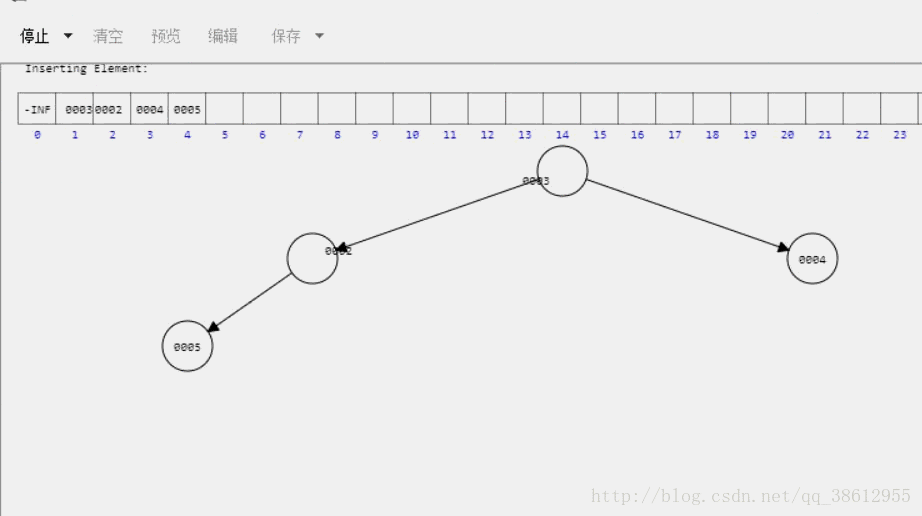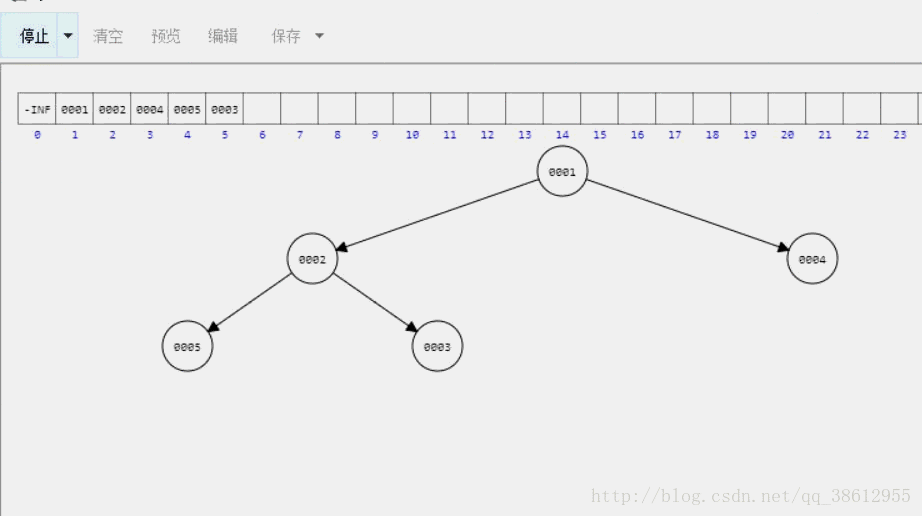
用堆实现优先级队列代码
priority_queue PQ;

#include<bits/stdc++.h>
#define INFTY (1<<30)
using namespace std;
#define MAX 2000001
#define INFIY (1<<30)
int h,a[MAX+1];
void maxheapify(int i) {
 int l,r,largest;
 l=2*i;
 r=2*i+1;
 if(l<=h&&a[l]>a[i]) largest=l;
 else largest=i;
 if(r<=h&&a[r]>a[largest]) largest=r;
 if(largest!=i) {
  swap(a[i],a[largest]);
  maxheapify(largest);
 }
}
int extract() {
 int max;
 if(h<1) return INFTY;
 max=a[1];
 a[1]=a[h];
 h--;
 maxheapify(1);
 return max;
}
void increasekey(int i,int key) {
 if(key<a[i]) return ;
 a[i]=key;
 while(i>1&&a[i/2]<a[i]) {
  swap(a[i],a[i/2]);
  i=i/2;
 }
}
void insert(int key) {
 h++;
 a[h]=-INFIY;
 increasekey(h,key);
}
int main() {
 cin>>h;
 char c[10];
 int key;
 while(scanf("%s",c)!=EOF) {
  if(c[0]=='e'&&c[1]=='n') break;
  if(c[0]=='i') {
   scanf("%d",&key);
   insert(key);
  } else printf("%d\n",extract());
 }
 return 0;
}