布隆过滤器

基本概念

布隆过滤器（Bloom Filter）是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法，缺点是有一定的误识别率和删除困难。

Google 爬虫 它要判断。哪些网页是被爬过来了的。

如果想要判断一个元素是不是在一个集合里，一般想到的是将所有元素保存起来，然后通过比较确定。链表，树等等数据结构都是这种思路. 但是随着集合中元素的增加，我们需要的存储空间越来越大，检索速度也越来越慢(O(n),O(logn))。不过世界上还有一种叫作散列表（又叫哈希表，Hash table）的数据结构（有一个动态数组，+ 一个 hash 函数）。它可以通过一个 Hash 函数将一个元素映射成一个位阵列（Bit array）中的一个点。这样一来，我们只要看看这个点是不是 1 就可以知道集合中有没有它了。这就是布隆过滤器的基本思想。

Hash 面临的问题就是冲突。假设 Hash 函数是良好的，如果我们的位阵列长度为 m 个点，那么如果我们想将冲突率降低到例如 1%, 这个散列表就只能容纳 m / 100 个元素。显然这就不叫空间效率了（Space-efficient）了。解决方法也简单，就是使用多个 Hash，如果它们有一个说元素不在集合中，那肯定就不在。如果它们都说在，虽然也有一定可能性它们在说谎，不过直觉上判断这种事情的概率是比较低的。

Bloom Filter 是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于这个集合。Bloom Filter 的这种高效是有一定代价的：在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误认为属于这个集合（false positive）。因此，Bloom Filter 不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter 通过极少的错误换取了存储空间的极大节省

总结起来说：bloomfilter，布隆过滤器：迅速判断一个元素是不是在一个庞大的集合内，但是他有一个弱点：它有一定的误判率

误判率：原本不存在于该集合的元素，布隆过滤器有可能会判断说它存在，但是，如果布隆过滤器判断说某一个元素不存在该集合，那么该元素就一定不在该集合内

优缺点

优点

相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数。另外, Hash 函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。

布隆过滤器可以表示全集，其它任何数据结构都不能；

k 和 m 相同，使用同一组 Hash 函数的两个布隆过滤器的交并差运算可以使用位操作进行。

能快速的判断元素存在不存在

远远的缩小存储数据的规模

缺点

但是布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。

另外，一般情况下不能从布隆过滤器中删除元素。我们很容易想到把位列阵变成整数数组，每插入一个元素相应的计数器加 1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。在降低误算率方面，有不少工作，使得出现了很多布隆过滤器的变种。

存在一定的误判率，那么在你不能容忍有错误率的情况，布隆过滤器不适用

布隆过滤器不支持删除操作

实现原理

布隆过滤器需要的是一个位数组(和位图类似, bytes 数组)和 K 个映射函数(和 Hash 表类似)，在初始状态时，对于长度为 m 的位数组 array，它的所有位被置 0。

“huangbo”.hashCode() => 3

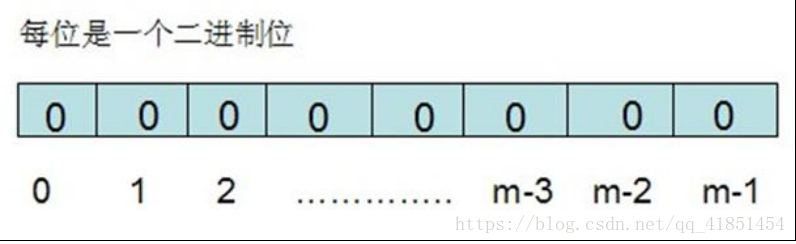
对于有 n 个元素的集合 S={S1,S2...Sn},通过 k 个映射函数{f1,f2,......fk}，将集合 S 中的每个元素Sj(1<=j<=n) 映射为 K 个 值 {g1,g2...gk} ， 然 后 再 将 位 数 组 array 中 相 对 应 的array[g1],array[g2]......array[gk]置为 1：

前两次是插入，插入的数据是“huangbo”“wangbaoqiang”

“huangbo”.hashCode1() => 2

“huangbo”.hashCode2() => 4

“wangbaoqiang” .hashCode1() => 3

“wangbaoqiang” .hashCode2() => 4

查询：“xuzheng”

“xuzheng”. hashCode1() => 4 有可能存在，有可能不存在，就算全部结果都是 1，也有可能不存在

“xuzheng”. hashCode2() => 1 能百分百确定，这个值一定不存在

只要所有的 hash 函数计算出来的值里面有一个值是 0 ，，我们就能确定这个 key = “xuzheng”他一定不存在与我们的集合里面

自定义一个布隆过滤器的时候需要做的事情：

1、 初始化一个位数组

2、 实现 K 个 hash 函数

3、 实现查询，和 插入操作

查询和插入操作需要做的事情：

对插入进来的值进行 hash 计算，有几个 hash 函数，就计算几次，每次计算出来的结果值，都根据这个值，去位数组里面把相应位置的 0 变成 1

对查询操作来说，只需要把你要查询的这个 key 值进行 k 个 hash 函数的调用，然后再判断计算出来的这个 k 个值对应的维数组上的值是不是有一个为 0,，，如果有一个为 0，那就表示，该 key 不在这个集合里面

N 个 hashcode() , N 位的 0 变成 1

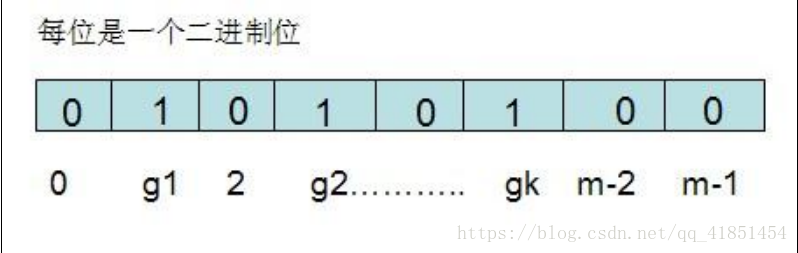
要查找某个元素 item 是否在 S 中，则通过映射函数{f1,f2,...fk}得到 k 个值{g1,g2...gk}，然后再判断 array[g1],array[g2]...array[gk]是否都为 1，若全为 1，则 item 在 S 中，否则 item 不在 S中。这个就是布隆过滤器的实现原理。

前面说到过，布隆过滤器会造成一定的误判，因为集合中的若干个元素通过映射之后得到的数值恰巧包括 g1,g2,...gk，在这种情况下可能会造成误判，但是概率很小。