二叉树（堆）

1、定义：二叉树是一个连通的无环图，并且每一个顶点的度不大于3。有根二叉树还要满足根结点的度不大于2。有了根结点之后，每个顶点定义了唯一的父结点，和最多2个子结点。然而，没有足够的信息来区分左结点和右结点。如果不考虑连通性，允许图中有多个连通分量，这样的结构叫做森林。

 

2、分类：

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。 

 

3、性质：

(1) 在非空二叉树中，第i层的结点总数不超过  , i>=1；

(2) 深度为h的二叉树最多有  个结点(h>=1)，最少有h个结点；

(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；

(4) 具有n个结点的完全二叉树的深度为  （注：[ ]表示向下取整）

(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

若I为结点编号则 如果I>1，则其父结点的编号为I/2；

 

树的遍历与创建，线索二叉树：https://blog.youkuaiyun.com/qq_41829060/article/details/81075565

 

如果2*I<=N，则其左儿子（即左子树的根结点）的编号为2*I；若2*I>N，则无左儿子；

如果2*I+1<=N，则其右儿子的结点编号为2*I+1；若2*I+1>N，则无右儿子。

(6)给定N个节点，能构成h(N)种不同的二叉树。

h(N)为卡特兰数的第N项。h(n)=C(2*n，n)/(n+1)。

(7)设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i 

 

*堆

1、定义：所有父节点的值小于子节点的值的完全二叉树称为最大堆，反之称为最小堆。

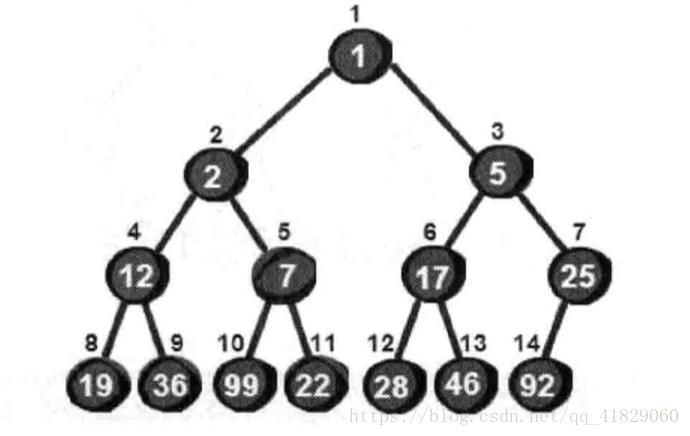
最小堆排序

//最小堆的建立及堆排序
#include<bits/stdc++.h>
using namespace std;
int h[101],n;

void sd(int i)
{
	int t,fg=0;
	while(fg==0&&i*2<=n) //在n内，继续查找 
	{
		if(h[i*2]<h[i]) //爸爸比左儿子打，交换 
		t=i*2;
		else t=i;
		
		if(i*2+1<=n) //比较右儿子 
		{
			if(h[i*2+1]<h[t])
			t=i*2+1;
		}
		
		if(i!=t)
		{
			swap(h[i],h[t]); //交换要变得元素 
			i=t; //继续寻找，很关键，不要写反 
		}
		else fg=1; //交换完成 
	}
}

void Creat()
{
	for(int i=n/2;i>=1;i--) //创建堆 
	sd(i);
}

int del() //删除最小的第一个元素 
{
	int t=h[1];
	h[1]=h[n];
	n--;
	sd(1);
	return t;
}

int main(void)
{
	int i,num;
	scanf("%d",&num);
	for(i=1;i<=num;i++)
	scanf("%d",&h[i]);
	n=num; //n会变，所以找num赋值 
	
	Creat();
	for(i=1;i<=num;i++)
	printf("%d ",del());
	return 0;
}

/*输入数据： 
14
99 5 36 7 22 17 46 12 2 19 25 28 1 92

输出数据 ： 
1 2 5 7 12 17 19 22 25 28 36 46 92 99
*/

最大堆排序

//堆排序 
#include<bits/stdc++.h>
using namespace std;
int h[101],n;

void sd(int i)
{
	int t,fg=0;
	while(i*2<=n&&fg==0)
	{
		if(h[i*2]>h[i])
		t=i*2;
		else t=i;
		
		if(i*2+1<=n)
		{
			if(h[i*2+1]>h[t])
			t=i*2+1;
		}
		
		if(i!=t) 
		{
			swap(h[i],h[t]);
			i=t;
		}
		else fg=1;
	}
} 

void Creat()
{
	for(int i=n/2;i>=1;i--)
	sd(i);
}

void del()
{
	int t=h[1];
	h[1]=h[n];
	n--;
	sd(1);
}

void Hash()
{
	while(n>1)
	{
		swap(h[1],h[n]);
		n--;
		sd(1);
	}
}

int main(void)
{
	int num,i;
	scanf("%d",&num);
	for(i=1;i<=num;i++)
	scanf("%d",&h[i]);
	n=num;
	
	Creat();
	Hash();
	
	for(i=1;i<=num;i++)
	printf("%d ",h[i]);
	return 0;
}
/*输入数据： 
14
99 5 36 7 22 17 46 12 2 19 25 28 1 92

输出数据 ： 
1 2 5 7 12 17 19 22 25 28 36 46 92 99
*/