LeetCode题目：34. 在排序数组中查找元素的第一个和最后一个位置

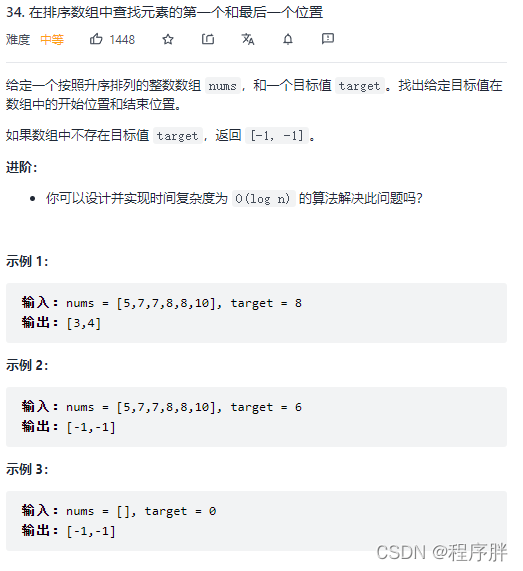
题目

题目解析

首先这是一个很明显的查找问题，查找问题很明显，我们直接用for循环遍历一遍就能找出来，但是这题目有个要求，需要找出这个数字最初的和最后的位置，这样的话，我们需要一个数组来记录字段，这样暴力方法就出来了

方法一：暴力解法

1. 首先我们需要一个数组，0用来存最初的，1用来存最后的，并且这个数组的初始值为-1
2. 然后我们遍历数组
   • 如果是我们目标的数字
     • 判断数组里0的值是否为-1，如果是则放入0的位置上，如果不是则放入1的位置上
   • 如果不是则跳过
3. 遍历完之后就把答案上传
4. 代码如下

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] ans = new int[]{-1,-1};
        for(int i=0;i<nums.length;i++){
            if(nums[i] == target){
                if(ans[0] == -1){
                    ans[0] = i; 
                }else{
                    ans[1] = i;
                }
            }
        }
        if(ans[0] != -1 && ans[1] == -1){
            ans[1] = ans[0];
        }
        return ans;
    }
}

• 总结：这样确实可以快速地求出答案，但是也看得出来性能确实不高，有没有更加简便的方法呢？有的，一般这种查找的题目，优先想的应该是二分查找，特别是这种有序的数组

方法二：二分查找

• 看到这个函数我就知道，题目很明显是想让我们使用二分查找，但是二分查找可以使用，但是我们如何使用二分查找，找到最初和最终的这个目标数字呢，很简单我们分开查找
• 算法思路：
  1. 首先我们需要一个二分查找函数，我们根据例子：5,7,7,8,8,10 来举例
     • 首先left 是指向 5的，然后right 是指向 10的 ，mid 是指向是 7
     • 然后判断发现 8 比 7大，然后left 就变成 mid +1 ，right保持不变
     • mid 就变成了 8 发现跟目标一样，所以 right = mid - 1
     • 最后发现 left = right ，循环结束
  2. 首个位置找到了，但是上面有个跟目标数字一样的位置，但是确实最终位置，如何进行判断呢，因为这是升序函数，所以当当前数字是目标数字的时候，我们通过一个boolean类型进行判断，如果是true的话说明我们再找最初的，就到左边的区间去找，如果是false的话，我们就要找最终的，就需要到右边的区间去找。
  3. 所以通过使用两个方法，就把位置找到了，通过判断是否符合标准再来输出答案
• 代码实现：

class Solution {
    public int[] searchRange(int[] nums, int target) {
    	int left = binarySearch(nums,target,true);
    	int right = binarySearch(nums, target, false) - 1;
        if (left <= right && right < nums.length && nums[left] == target && nums[right] == target) {
            return new int[]{left, right};
        } 
        return new int[]{-1, -1};
 
    }
    
    public int binarySearch(int[] nums, int target, boolean lower) {
    	int left = 0;
    	int right = nums.length - 1;
    	int ans = nums.length;
    	while(left<=right) {
    		int mid = (left+right)/2;
    		if (nums[mid] > target || (lower && nums[mid] >= target)) {
				right = mid - 1;
                ans = mid;
			}else {
				left = mid + 1;
			}
    	}
		return ans;
    }
}

• 总结：从结果上来看，时间确实快，但是因为数据量不大，所以不够明显，但是总的来说，对于有序数组还是二分查找比较适合，因为能够快速缩小范围。