算法分析：统计素数

前言

题目网址：https://leetcode-cn.com/problems/count-primes/

第一种方法

• 这道题最简单的方法就是暴力解法，很简单，就是从 1 到 n 一个一个判断，然后把结果返回，不多说了直接上代码

class Solution {
    public int countPrimes(int n) {
        int ans = 0;
        for (int i = 2; i < n; ++i) {
            ans += isPrime(i) ? 1 : 0;
        }
        return ans;
    }

    public boolean isPrime(int x) {
        for (int i = 2; i * i <= x; ++i) {
            if (x % i == 0) {
                return false;
            }
        }
        return true;
    }
}

• leetcode超出时间限制了，但是只是官网给的答案，我也想不通

第二种方法

• 这次我是长见识了，学习到一种新的方法埃氏筛选法，这个方法就是利用了素数和非素数的特性，非素数的特性就是可以因式分解，所以我们就要利用这个特点，通过前期像 2X3 2x4 2x5 等等这种小的来排除非素数。也就是通过空间换时间的做法，来提升性能。

class Solution {
    public int countPrimes(int n) {
        boolean[] dp = new boolean[n+1];
        int count = 0;
        for(int i=2;i<n;i++){
            if(!dp[i]){
                count++;
            }
            for(int j=2*i;j<n;j+=i){
                   dp[j] = true; 
            }
        }
        return count;
    }
}

• 这个方法还能优化，就是看下图的例子
  
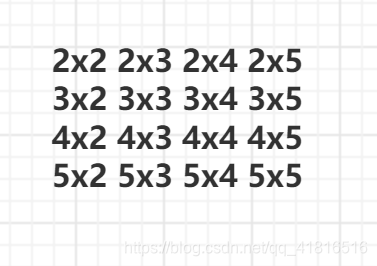
• 上图的例子中我们发现2x2 2x3 2x4 2x5 这些数字重复访问，因为我们后面也会访问到，那我们就大胆想象，假设我就把 i2 改成 ii 这不就砍掉了一半，性能就能提升上去了

class Solution {
    public int countPrimes(int n) {
        boolean[] dp = new boolean[n];
        int count = 0;
        for(int i=2;i<n;i++){
            if(!dp[i]){
                count++;
                if((long)i*i < n) {
                    for(int j= i*i;j<n;j+=i){
                        dp[j] = true; 
                    }
                }
            }
        }
        return count;
    }
}

• 性能提升一大截

总结

暴力解法其实就是根据题目意思解决问题，但是现在大数据的时代下，我们需要处理的数量可能很大所以需要更好的性能，所以还是需要多学习。