LeetCode题目：剑指 Offer 47. 礼物的最大价值

原创于 2020-07-08 16:06:28 发布 · 158 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #动态规划

LeetCode 专栏收录该内容

50 篇文章

订阅专栏

本文解析了LeetCode上一道经典动态规划问题——礼物的最大价值路径。在一个只能向右或向下的矩阵中，如何找到从起点到终点路径上礼物价值最大的路线。通过使用动态规划方法，我们定义了一个状态转移方程，解决了这一问题，并提供了详细的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

题目链接：https://leetcode-cn.com/problems/li-wu-de-zui-da-jie-zhi-lcof/
题目解析：
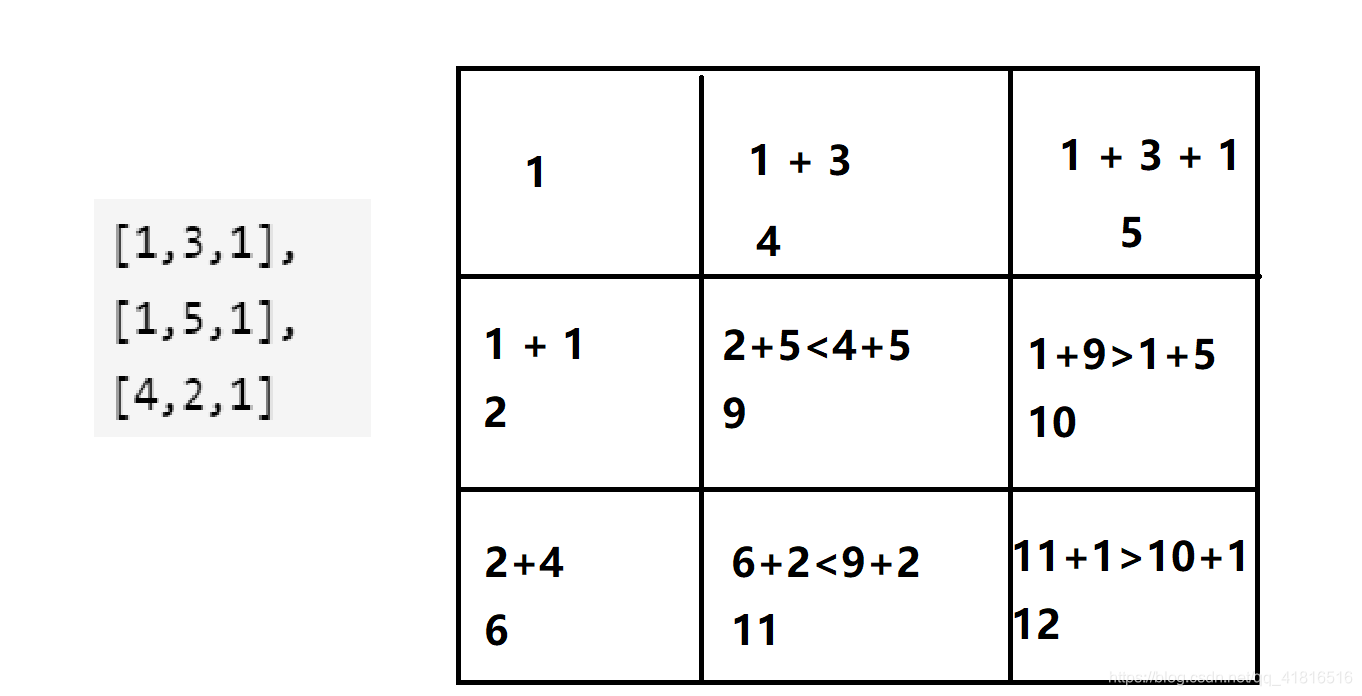
- 在一个矩阵里面，从第一个方块走到最后一个，只能向右或向下，求怎么走才能拿到礼物最大。
- 用dp公式dp[i][j] = max(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j])，判断第 i 行，第 j 个方块中，是上面的方块得到的权重大，还是左边过来的权重大。

代码

class Solution {
    public int maxValue(int[][] grid) {
    	//创建资源
        int length = grid[0].length;
        int[][] dp = new int[grid.length][length];
        //循环遍历
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
            	//如果是第一个，就赋值
                if(j==0&&i==0)
                        dp[i][j]=grid[i][j];
                //如果是第一行，只能向右走
                else if(j==0&&i>0)
                    dp[i][j] = dp[i-1][j]+grid[i][j];
                //如果是第一列，只能想下走
                else if(i==0&&j>0)
                    dp[i][j] = dp[i][j-1]+grid[i][j];
                //如果都不是，就可以选择向下或者向右
                else{
                    dp[i][j] = Math.max(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]);
                }
            }
        }
        return dp[grid.length-1][length-1];
    }
}