数据结构------------线性表（上篇）

最新推荐文章于 2022-04-13 07:14:20 发布

原创最新推荐文章于 2022-04-13 07:14:20 发布 · 378 阅读

5 ·

CC 4.0 BY-SA版权

数据结构专栏收录该内容

33 篇文章

订阅专栏

本文详细介绍了线性表的基本概念、特点及其类型定义，并通过顺序表的实例深入讲解了线性表的各种基本操作，包括初始化、遍历、取值、查找、插入和删除等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

线性表：由n（n>=0）个数据特性相同的元素构成的有限序列

线性表中的袁旭个数n(n>=0)定义为线性表的长度，n=0时为空表

非空的线性表或线性结构特点：

1）存在唯一的一个数被称为“第一个”的数据元素；

2）存在唯一的一个数被称为“最后一个”的数据元素；

3）除第一个之外，结构中的每个数据元素均只有一个前驱（predecessor）;

4)除最后一个之外，结构中的每个数据元素均只有一个后继（successor）;

线性表的类型定义

//ADT = Abstract Date Type 抽象数据类型

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------

ADT List{

数据对象：D={ai | ai∈ElemSet,i=1,2,3,...,n,n>=0}

数据关系：R={< > = <= >= !=.....}

基本操作：

IntList(&L) //操作结果初始化构造一个空的线性表L

DestroyList(&L) //操作结果销毁线性表L

ClearList(&L) //操作结果置空将线性表重置为空表

ListInsert(&L,i,e) //操作结果插入在L中第i位置之前插入新的数据元素e,L的长度加一。

ListDelete(&L,i) //操作结果删除删除L的第i个数据元素，L 的长度减一。

//-------------分割线前面都是对L的操作即L的内容会随这些操作而发生变化------------

ListEmpty(L) //操作结果判空即若L是空表，则返回true,否则返回false

ListLength(L) //操作结果返回L中数据元素的个数

GetElem(L,i,&e) //操作结果取值用e返回L中第i个数据元素的值

LocateElement(L,e) //操作结果定位返回L中第一个值与e相同的元素在L中的位置，若不存在则返回0

PriorElem(L,cur_e,&npre_e) //操作结果前驱若cur_e是L的数据元素，且不是第一个,则用pre_e 返回其前驱，否则操作失败 pre_e无定义

NextElem(L,cur_e,&next_e) //操作结果后驱若cur_e是L的数据元素，且不是最后一个,则用next_e 返回其前驱，否则操作失败， next_e无定义

TraverseList(L) //操作结果遍历对线性表L进行遍历，在遍历过程中对每个结点访问一次

}ADT List

------------------------------------------------------其实这些函数完全可以按照自己的想法来定义-------------------------------------------------------

顺序表：线性表按顺序存储（随机存取）

链式表：线性表按链式存储（顺序存取）

一、

//---------------顺序表的存储结构--------------

#define MAXSIZE 100    //分配数组空间大小 当然可以自己定义
typedef struct
{
	ElemType *elem;  //存储空间的基地址 
	                //ElemType指的是数组的类型可根据实际需要更换成 int char double 等
	int length;     //当前长度
	                //同时也指的是逻辑长度  跟数组下标错1 
 } SqList;         //顺序表的结构类型为SqList

逻辑长度（从1开始）与数组下标（从0开始）存在偏差

假设定义了一个顺序表结构体类型的变量 SqList L;

访问其数组的第一个元素即 L.elem[0]

访问其数组的最后一个元素即 L.elem[L.length-1]

二、顺序表中基本操作的实现

ps: 这里return 0 可不是主函数里面的return 0 奥

1、初始化

【算法描述】

Status InitList(SqList &L)
{
	L.elem=new ElemType[MAXSIZE] //为顺序表分配一个大小为MAXSIZE大小的数组空间 
	if(!L.elem) exit (-2);       //储存分配失败退出
                                 //exit() 直接结束当前进程 括号里面是0正常结束 否为不正常结束
	L.length=0;                  //空表长度为0
	return 1;
}

2、遍历

【算法描述】

void TraverseList(SqList L)
{
    for(int i=0;i<L.length;i++)
     cout<<L.elem[i]<<endl;     //遍历输出 
}

【指针】 -------皮一下很开心罒ω罒

void TraverseList(SqList L)
{
	ElemType *p; 
    for(p=L.elem;p<L.elem+L.length-1;p++)
     cout<<*p<<endl;     //遍历输出 
}

3、取值

【算法描述】

Status GetElem(SqList L,int i,ElemType &e)
{
	if(i<1||i>L.length)  
	    return 0;     //判断i值是否合理   
	e=L.elem[i-1];    //我们要取的是第i号元素  在数组中的下标是i-1 嘛 
	return 1; 
 }

【算法分析】

一遍过自然时间复杂度为O(1)

4、查找

【算法描述】

int  LocateElem(SqList L,ElemType e)
{  //在顺序表L中查找值为e的数据元素  返回其逻辑位置 
	for (int i=0;i<L.length;i++)
	 if(L.elem[i]==e) return i+1;  //查找成功 返回逻辑位置i+1
	return 0; 
 }

查找用指针的话会相对来说稍微麻烦了点还需要再加个记录位置的计数器所以就不写了=_=||

【算法分析】

假设每个元素查找的概率相等

最好的情况下查找1次最坏的情况下查找n次

总的查找次数为1+2+3+....+n=(1+n)*n/2

一共有n种可能

ASL（Average Search Length 平均查找长度）=（1+n）/ 2

时间复杂度为O(n)

5、插入

【算法描述】

Status ListInsert(SqList &L,int i,ElemType e)
{
      if((i<1)||(i>L.length+1))	 return -2;  //i的位置不合法 
      if(L.length==MAXSIZE) return -2;       //当前储存空间已满 
      for(int j=L.length-1;j>=i-1;j--)       
       L.elem[j+1]=L.elem[j];                //插入位置及之后的元素后移 
       L.elem[i-1]=e;                        //将新元素e放入第i个位置  
	                                         //也可以写成L.elem[j+1]=e; 循环结束后j的位置为i-2    
       L.length++;                           //表长加1 
       return 1;
 }

关于插入数e的位置还是画个图吧更容易理解为什么是i-1 或者是j+1 ^_^

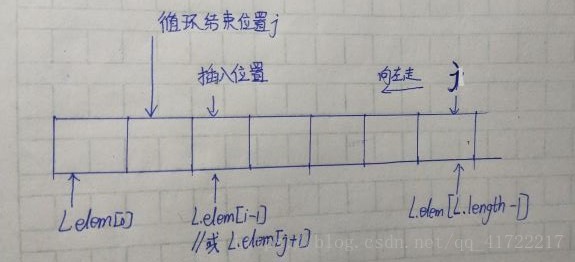
【指针】

Status ListInsert(SqList &L,int i,ElemType e)
{
	  SqList *p;
      if((i<1)||(i>L.length+1))	 return -2;  //i的位置不合法 
      if(L.length==MAXSIZE) return -2;       //当前储存空间已满 
      for(p=L.length-1;p>=L.elem+i-1;p--)       
       *(p+1)=*p;                //插入位置及之后的元素后移 
       *(p+1)=e;                        //将新元素e放入第i个位置  
	                                        
       L.length++;                           //表长加1 
       return 1;
 }

【算法分析】

假设每个元素查找的概率相等

最好的情况下移动0次最坏的情况移动下n次

总的查找次数为0+1+2+3+....+n=n*(1+n)/2

一共有n+1种可能

ASL（Average Search Length 平均查找长度）= n / 2

时间复杂度为O(n)

6、删除

【算法描述】

Status ListDelete(SqList &L,int i)
{
	  
      if((i<1)||(i>L.length))	 return -2;  //i的位置不合法 
      for(int j=i;j<=L.length-1;j++)       
        L.elem[j-1]=L.elem[j];               //后一个元素覆盖前一个元素 
	                                        
       L.length--;                           //表长减1 
       return 1;
 }

【指针】

Status ListDelete(SqList &L,int i)
{
	  SqList *p; 
      if((i<1)||(i>L.length))	 return -2;  //i的位置不合法 
      for(p=L.elem+i;p<=L.elem+L.length-1;p++)       
       *(p-1)=*p;                            //后一个元素覆盖前一个元素 
	                                        
       L.length--;                           //表长减1 
       return 1;
 }

【算法分析】

假设每个元素查找的概率相等

最好的情况下移动0次最坏的情况移动下n-1次

总的查找次数为0+1+2+3+....+n-1=(n-1)*n/2

一共有n种可能

ASL（Average Search Length 平均查找长度）= (n-1) / 2

时间复杂度为O(n)

简单顺序表（int数据）

#include<iostream>
#define MAXSIZE 100
using namespace std;
typedef struct
{
	int *elem;
	int length;
}SqList;
int InitList(SqList &L)//初始化 
{
	L.elem=new int[MAXSIZE];
	if(!L.elem) return 0;
	L.length=0;
	return 1;
}
int ClearList(SqList &L)//重置为空表 
{
	L.length=0;
	return 1;
 } 

int ListLength(SqList L)//长度
{
	return L.length;
}

int GetElem(SqList L,int i,int &e)//取值 
{
	if(i<1||i>L.length) return 0;
	e=L.elem[i-1];return 1;
}
int LocateElem(SqList L,int e)//查找 
{
	for(int i=0;i<L.length ;i++)
	{
		if(L.elem[i]==e) return i+1;
	}
	return 0;
 }
int PriorElem(SqList L,int cur_e,int &pre_e) //返回前驱 
{
	if(cur_e!=L.elem[0]) 
	{
		for(int i=0;i<L.length ;i++)
		{
			if(L.elem [i]==cur_e)
			 {
			  pre_e= L.elem[i-1];
			  return 1;
		     }
		}
	}
	return 0;
}
int NextElem(SqList L,int cur_e,int &next_e) //返回后继 
{
	if(cur_e!=L.elem[L.length -1]) 
	{
		for(int i=0;i<L.length ;i++)
		{
			if(L.elem [i]==cur_e)
			 {
			 next_e= L.elem[i+1];
			 return 1;
		     }
		}
	}
	return 0;
}
void ListInsert(SqList &L,int i,int e) //插入 
{
	for(int j=L.length-1 ;j>=i-1;j--)
	L.elem [j+1]=L.elem [j];
	L.elem [i-1]=e;
	L.length ++;
}
void ListDelete(SqList &L,int i)//删除
{
	for(int j=i-1;j<L.length ;j++) 
	L.elem [j]=L.elem [j+1];
	L.length --; 
} 

int main()
{
	cout<<"1.初始化"<<endl;
	cout<<"2.置空"<<endl;
	cout<<"3.输入"<<endl;
	cout<<"4.长度"<<endl;
	cout<<"5.取值"<<endl;
	cout<<"6.查找"<<endl;
    cout<<"7.返回前驱"<<endl;
	cout<<"8.返回后继"<<endl;
	cout<<"9.插入"<<endl;
	cout<<"10.删除"<<endl;
	cout<<"11.遍历"<<endl;
	cout<<"0.退出"<<endl<<endl;
	int choose;
     cout<<"请选择你的操作:";
	 cin>>choose;
	while(choose)
	{
	SqList  L;
	int n,i,e;
	switch(choose){
	
     case 1://初始化
		 if(InitList(L)==1) 
		 cout<<"初始化成功"<<endl<<endl;
		 break;

	 case 2://置空
	     if(ClearList(L)==1)
		 cout<<"置空成功"<<endl<<endl;
		 break;

	 case 3://输入
		 {cout<<"输入数组长度：";
         cin>>n;int p;
    	 cout<<"输入各个元素：";
		 for(p=0;p<n;p++)
		  { 
			 cin>>L.elem[p];
			 L.length++;
		 }
		 cout<<endl;
		 }
		 break;

	 case 4://长度

         cout<<"该线性表中元素个数为"<< ListLength(L)<<"个"<<endl<<endl;
		 break;
	 case 5://取值
	     cout<<"请输入您要取值的位置："; 
         cin>>i;
         if(GetElem(L,i,e))
	     cout<<"第"<<i<<"个元素是"<<e<<endl<<endl;
	     else
	     cout<<"取值失败！"<<endl<<endl; 
		 break;
	 case 6://查找
         int e;
         cout<<"请输入您要查找的元素：";
		 cin>>e;
         if(LocateElem(L,e)==0) 
         cout<<"查无此元素"<<endl<<endl;
	     else 
         cout<<"元素"<<e<<"在线性表的位置是" <<LocateElem(L,e)<<endl<<endl;
	     break;
	 case 7://前驱 
		 {int cur_e,pre_e;
		 cout<<"请输入一个元素：" ;
	     cin>>cur_e; 
		 int temp=cur_e;
         if(PriorElem(L,cur_e,pre_e))
         cout<<"元素"<<temp<<"的前驱是"<<pre_e<<endl<<endl;
		 else
		 cout<<"返回失败！"<<endl<<endl;}
		 break;
	 case 8://后继
		 {int next_e,cur_e; 
		 cout<<"请输入一个元素：";
         cin>>cur_e;
		 int temp=cur_e;
         if(NextElem(L,cur_e,next_e))
		 cout<<"元素"<<temp<<"的后继是"<<next_e<<endl<<endl;
		 else
		 cout<<"返回失败！"<<endl<<endl;}
		 break;
	 case 9://插入
	     cout<<"请分别输入带插入元素的位置和元素值："; 
	     cin>>i>>e;
         if(i<=L.length&&i>=0)
		 {
			 ListInsert(L,i,e);
			 cout<<"插入成功"<<endl<<endl;
		 }
		 else
			 cout<<"插入失败"<<endl<<endl;
		 break;
	 case 10://删除
	     cout<<"请输入要删除的元素位置："; 
	     cin>>i;
		 if(i<=L.length&&i>0)
		 {
			  ListDelete(L,i); 
			  cout<<"删除成功"<<endl<<endl;
		 }
		 else
			 cout<<"删除失败"<<endl<<endl;  
		 break;
	 case 11://遍历
	    int q=0;
	    cout<<"该线性表为：";
	    for(int p=0;p<L.length;p++)
		{
	    	cout<<L.elem[p]<<" ";
		    q++;
		   if(q==10)
		   {
			cout<<endl;
			q=0;
		   }
		}
		cout<<endl<<endl;
		 break;
	}
	cout<<"请选择你的操作:";
	 cin>>choose;
	}
	cout<<"程序已退出"<<endl;
	return 0;
 }

下篇链式表 o(╥﹏╥)oo(╥﹏╥)oo(╥﹏╥)o

下篇见￣へ￣