java练习day06-Debug-进制-二维数组-杨辉三角

Day06

Debug

Debug概述：

​ Debug是供程序员使用的程序调试工具，它可以用于查看程序的执行流程，也可以用于追踪程序执行过程来调试程序。

Debug操作流程

​ Debug调试，又被称为断电调试，断点其实是一个标记，告诉Debug从标记的地方开始查看

1. 如何加断点

   选择要设置断点的代码行，在行号的区域后面单击鼠标左键即可。如下图，红点处就是断点，代码开始执行后会停在此处；

   

2. 如何运行加了断点的程序

   在代码区域右键Debug执行，如下图：

   

3. 看哪里

   看Debug窗口，如下图：

   

   看console窗口，如下图：

   

4. 点哪里

   点Step Into(F7)这个箭头，也可以直接按F7，如下图：

   

   点stop结束，如下图：

   

5. 如何删除断点

   选择要删除的断点，单击鼠标左键即可。

   如果是多个断点，可以每一个再点击一次。也可以一次性全部删除。如下图：（补充：选中第一个框，再点击减号就会删掉所有断点）

   

进制

进制介绍

• 进制指进位制，是人们规定的一种进位方式；表示某一位置上的数，运算时是逢X进一位。如十进制逢十进一，二进制逢二进一，八进制逢八进一…
• 常见进制：二进制、八进制、十进制、十六进制

二进制

• 二进制数据是用0和1两个数码来表示。例如：0101000，进位规则是“逢二进一”，借位规则是“借一当二”。

• 二进制计算：0011+1

  • 

• 二进制计算：0010-1

  • 

八进制和十六进制

• 八进制：采用0,1,2,3,4,5,6,7八个数字，逢八进一
• 十六进制：用数字0到9和字母A到F(或a_{f)表示，其中：A}F表示10~15，这些被称作十六进制。

不同进制的书写格式

• 十进制：Java中，数值默认都是十进制，不需要加任何修饰；
• 二进制：数值前面以0b开头，b大小写都可以；（这里的0是数字0，下同）
• 八进制：数值前面以0开头；
• 十六进制：数值前面以0x开头，x大小写都可以。
• 注意：以上内容是jdk7版本后才被支持

进制转换

• 二进制到十进制的转换
• 公式：系数*基数的权次幂相加
  • 系数：每一位上的数
  • 基数：几进制就是几
  • 权：从数值的右侧，以0开始，逐个+1增加
• 例如：

• 十六进制到十进制转换
• 公式：与二进制向十进制转换相同
• 例如：

• 八进制到十进制转换

• 转换规则与前面相同

• 十进制到二进制的转换

• 公式：除基取余

  ​ 使用原数据，不断地除以基数(几进制，基数就是几)得到余数，直到商为0，再将余数倒着拼起来即可。

  • 例如：将十进制数21，转换为二进制，如下图：

  

• 十进制到十六进制转换

• 公式：除基取余

  • 例如：将十进制数68转换十六进制，如下图：

  

• 十进制到八进制转换

• 规则同上

快速进制转换法

• 8421码：

  ​ 8421码又称BCD码，是BCD代码中最常用的一种

  ​ BCD：二进制码十进制数

  ​ 在这种编码方式中，每一位二进制值的1都是代表一个固定数值，把每一位的1代表的十进制数加起来得到的结果就是它所代表的十进制数。

  • 

• 

• 

原码反码补码

​ 注意：计算机中的数据，都是以二进制补码的形式在运算，而补码则是通过反码和原码推算出来的。

• 原码（可直观看出数据大小）

  ​ 就是二进制定点表示法，即最高位为符号位，【0】表示正，【1】表示负，其余位表示数值的大小。

  ​ 通过一个字节表示+7和-7，代码：byte b1 = 7；byte b2 = -7；

  ​ 一个字节等于8个比特位，也就是8个二进制位

  ​ 0(符号位) 0000111

  ​ 1(符号位) 0000111

• 反码

  ​ 正数的反码与其原码相同；负数的反码是对其原码逐位取反，但符号位除外。

• 补码（数据以该状态进行运算）

  ​ 正数的补码与其原码相同；负数的补码是在其反码的末位加1。

• 总结：

  • 原码：看数据
  • 反码：转数据
  • 补码：运算数据

案例分析

byte b = (byte) 130;
System.out.println(b);
输出结果为：-126

位运算符

位运算符介绍

• 位运算符指的是二进制位的运算，先将十进制数转成二进制后再进行运算。

• 在二进制位运算中，1表示true，0表示false。

  • & 位与：遇false则false，遇0则0

      00000000 00000000 00000000 00000110  //6的二进制
    & 00000000 00000000 00000000 00000010  //2的二进制
      00000000 00000000 00000000 00000010  //结果：2
    

  • | 位或：遇true则true，遇1则1

  • ^ 位异或：相同为false，不同为true

  • ~取反：全部取反，0变1,1变0（也包括符号位）

      00000000 00000000 00000000 00000110  //6的二进制补码
    ~ 11111111 11111111 11111111 11111001
    
    -                                   1  //-1求反码
      11111111 11111111 11111111 11111000  //反码推原码
      10000000 00000000 00000000 00000111  //-7
    

位移运算符

• << 有符号左移运算，二进制位向左移动，左边符号位丢弃，右边补齐0

  • 运算规律：向左移动几位，就是乘以2的几次幂

    00000000 00000000 00000000 00001100  //12的二进制
    

• >> 有符号右移运算，二进制位向右移动，使用符号位进行补位

  • 运算规律：向右移动几位，就是除以2的几次幂

    00000000 00000000 00000000 00000011  //3的二进制
    

• >>> 无符号右移运算符，无论符号位是0还是1，都补0

  • 运算规律：

    10000000 00000000 00000000 00000110  //-6的二进制
    

• 异或运算的特点

  • 一个数，被另外一个数，异或两次，该数本身不变。

案例：数据交换

需求：已知两个整数变量a=10，b=20，在不使用第三方变量的情况下交换a和b的值；

public class DebugTest1 {
    public static void main(String[] args) {
        //定义两个变量
        int a = 10;
        int b = 20;
        a = a ^ b;  //a=10^20
        b = a ^ b;  //b=10^20^20
        a = a ^ b;  //a=10^20^10
        System.out.println("a="+a);
        System.out.println("b="+b);
    }
}
/*
	结果是：
	a=20
	b=10
*/

案例：反转

需求：已知一个数组arr={19,28,64,36,49},用程序实现把数组中的元素值交换，交换后的数组arr={49,36,64,28,19}，并在控制台输出交换后的数组元素。

/*
	1.定义两个变量，start和end来表示开始和结束的指针；
	2.确定交换条件，start<end允许交换
	3.循环中编写交换逻辑代码
	4.每一次交换完成，改变两个指针所指向的索引start++，end--
	5.循环结束后，遍历数组并打印，查看反转后的数组
*/
public class Fanzhuan {
    public static void main(String[] args) {
        int[] arr = {19,28,64,36,49};
        exchange(arr);
        System.out.println("交换后的数组元素为：");
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+" ");
        }
    }
    public static void exchange(int[] arr){
        //将数组两端的元素进行交换
        for (int start = 0,end = arr.length-1; start < end; start++,end--) {
            int temp = arr[start];
            arr[start] = arr[end];
            arr[end] = temp;
        }
    }
}

结果：

二维数组

概述：

​ 二维数组也是一种容器，不同于一维数组，该容器存储的都是一位数组容器；

二维数组定义格式：

格式1:数据类型[][]变量名;
范例:int[][] arr;
格式2:数据类型 变量名[][];
格式3:数据类型[] 变量名[];
范例:int arr[][];
范例:int[] arr[];

二维数组动态初始化

格式:数据类型[][] 变量名 = new 数据类型[m][n];
	m表示这个二维数组可以存放多少个一位数组
	n表示每个一维数组可以存放多少个元素
范例:int[][] arr = new int[3][4];
	该数组可以存放3个一维数组，每个一维数组中可以存放4个int类型的元素

二维数组存储一维数组的时候，存储的是一维数组的内存地址；

二维数组访问元素的细节问题

• 举例说明：可以向一个二维数组arr[3] [3]中直接添加一个一位数组arr[1]=arr1[4]而不会报错，因为此处是地址的替换，即将arr[1]所指的地址改为arr1[4]的地址；直接arr[1] [3]=5,则会报错，因为数组中不存在arr[1] [3]这个元素，会发生越界错误。

二维数组静态初始化

完整格式:数据类型[][] 变量名 = new 数据类型[][]{{元素1,元素2,...},{元素1,元素2,...},...};
简化格式:数据类型[][] 变量名 = {{元素1,元素2,...},{元素1,元素2,...},...};

二维数组遍历

需求：已知一个二维数组arr = {{11,22,33},{44,55,66}};遍历该数组，取出所有元素并打印；

/*
	1.遍历二维数组，取出里面每一个一位数组
	2.在遍历过程中，对每一个一维数组继续完成遍历，获取内部存储的每一个元素
*/
public class DoubleArr {
    public static void main(String[] args) {
        int[][] arr = {{11,22,33},{44,55,66}};
        for(int i=0;i<arr.length;i++){
            //内循环执行完一圈，二位数组中的一组一维数组遍历完毕
            for(int j=0;j<arr[i].length;j++){  //arr[i].length表示二维数组中索引为i的一维数组的长度
                System.out.print(arr[i][j]+" ");
            }
            System.out.println(); //遍历完一个一维数组后换行
        }
    }
}

二维数组求和

案例：公司年销售额求和，某公司季度和月份统计数据如下：单位(万元) 第一季度：22,66,44；第二季度：77,33,88；第三季度：25,45,65；第四季度：11,66,99

/*
	1.定义求和变量，准备记录最终累加结果
	2.使用二维数组来存储数据，每个季度是一个一维数组，再将4个一维数组装起来
	3.遍历二维数组，获取所有元素，累加求和
	4.输出最终结果
*/
public class DoubleArr {
    public static void main(String[] args) {
        int[][] arr = {{22,66,44},{77,33,88},{25,45,65},{11,66,99}};
        int sum = 0;
        for(int i=0;i<arr.length;i++){
            //内循环执行完一圈，二位数组中的一组一维数组遍历完毕
            for(int j=0;j<arr[i].length;j++){  //arr[i].length表示二维数组中索引为i的一维数组的长度
                sum += arr[i][j];
            }
        }
        System.out.println("公司年销售额为："+sum+"万元");
    }
}

结果:

练习1

自定义一个方法，根据用户键盘录入的行和列，能打印出对应行对应列的矩形;

例如:

当用户希望打印3行5列打印出效果如下:

*****
*****
*****

当用户希望打印4行8列打印出效果如下:

********
********
********
********

import java.util.Scanner;

public class DoubleArr {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.print("请录入要打印的行数：");
        int i = sc.nextInt();
        System.out.print("请录入要打印的列数：");
        int j = sc.nextInt();
        print(i,j);  //调用print方法并参数行和列传递给print方法
    }
    public static void print(int i,int j){
        for(int a=0;a<i;a++){
            //内循环循环一圈打印一行
            for(int b=0;b<j;b++){
                System.out.print("*");
            }
            System.out.println(); //打印一行后回车
        }
    }
}

结果：

练习2

自定义一个方法，根据用户键盘录入的行，能打印出对应行的直角三角形形;

例如:

当用户希望打印3行的三角形效果如下:

*
**
***

当用户希望打印5行的三角形效果如下:

*
**
***
****
*****

import java.util.Scanner;
/*
    经分析知：所有三角形均是第一行打印一次，第二行打印两次，第三
    行打印三次，即第几行打印几次，所以每一行打印次数由行号（外层
    循环）决定
* */
public class DoubleArr {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.print("请录入要打印的行数：");
        int num = sc.nextInt();
        print(num);
    }
    public static void print(int num){
        for(int i=1;i<=num;i++){
            //使内层循环次数与行号相等
            for(int j=1;j<=i;j++){
                System.out.print("*");
            }
            System.out.println();
        }
    }
}

结果：

练习3

请自定义一个方法,在方法中打印出九九乘法表,并在main方法中调用自定义的方法;

/**
 * 根据乘法表的规律可知，第1行是1*1；第2行是
 * 1*2,2*2；第3行是1*3,2*3,3*3；所以第n行是
 * 1*n,2*n,3*n,...,n*n。因此，此题和练习2相
 * 似，内循环由外循环决定
 */
public class Circle {
    public static void main(String[] args) {
        nineTable();
    }
    public static void nineTable(){
        for(int i=1;i<=9;i++){
            for (int j=1;j<=i;j++){
                int ji = j*i;
                if(ji<10){  //这里加条件知识为了让样式对齐
                    System.out.print(j+"*"+i+"="+(j*i)+"  ");
                }else {
                    System.out.print(j+"*"+i+"="+(j*i)+" ");
                }
            }
            System.out.println();
        }
    }
}

结果：

练习4

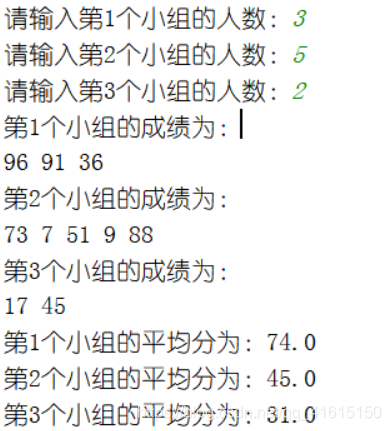
假如一个班级中有3个小组,第一个小组中有3个人,第二个小组中有5个人,第三个小组中有2个人,请分别定义两个方法,一个方法使用代码随机给三个小组中的每个人保存一个1-100之间的随机数作为分数,另一个方法计算出每个小组内成绩的平均分;

import java.util.Random;
import java.util.Scanner;
/*
    根据题意，可以定义一个二维数组，然后调用方
    法为二维数组赋值，最后遍历数组求平均值
 */
public class ScoreRandom {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        //定义二维数组存放三个小组
        int[][] arr = new int[3][];
        //循环录入三个小组的人数，并定义二维数组内一维数组的长度
        for(int i=0;i<3;i++){
            System.out.print("请输入第"+(i+1)+"个小组的人数：");
            int j = sc.nextInt();
            arr[i] = new int[j];
        }
//        //定义三个数组分别存放三个小组的分数
//        int[] arr1 = new int[3];
//        int[] arr2 = new int[5];
//        int[] arr3 = new int[2];
//        //将二维数组指向三个数组
//        arr[0]=arr1;
//        arr[1]=arr2;
//        arr[2]=arr3;
        randomScore(arr);
        for(int i=0;i<arr.length;i++){
            System.out.println("第"+(i+1)+"个小组的成绩为：");
            for(int j=0;j<arr[i].length;j++){
                System.out.print(arr[i][j]+" ");
            }
            System.out.println();
        }
        double[] avg = randomAvg(arr);  //调用方法并接收其返回的数组
        for(int i=0;i<avg.length;i++){
            System.out.println("第"+(i+1)+"个小组的平均分为："+avg[i]);
        }
    }
    public static void randomScore(int[][] arr){
        Random r = new Random();
        //循环为二维数组随机赋值
        for(int i=0;i<arr.length;i++){
            for (int j=0;j<arr[i].length;j++){
                arr[i][j]=r.nextInt(100)+1;
            }
        }
    }
    public static double[] randomAvg(int[][] arr){
        double[] avg = new double[arr.length];
        //内循环求每个小组的分数和
        for(int i=0;i<arr.length;i++){
            int sum = 0;
            for(int j=0;j<arr[i].length;j++){
                sum += arr[i][j];
            }
            //求每个小组的平均值并存入数组
            avg[i] = sum/arr[i].length;
        }
        return avg;
    }
}

结果：

练习5

创建方法，打印出杨辉三角形（要求打印出10行）

				1
			1		1
		1		2		1
	1		3		3		1
1		4		6		4		1

分析：两数字间的位置差值为2

1 m

2 m-1 m+1

3 m-2 m m+2

4 m-3 m-1 m+1 m+3

5 m-4 m-2 m m+2 m+4

import java.util.Scanner;
/*
    分析知：杨辉三角有几行，则他最后一行就有几个数，即n行
    杨辉三角，其第n行有n个数，n-1个空格，其中间数的位置在
    从左至右第n个字符处，同样其第一行的字符1,也位于这个位
    置；又可以发现，每个数是其上面那一行的位于其左上和右上
    两个数的和，即：如果这个数是该行第n个字符，则它的值就
    等于其上面那一行的第n-1个字符和第n+1个字符的和。
 */
public class Yanghui {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.print("请输入要打印的杨辉三角的行数：");
        int m = sc.nextInt();
        //每一列数字里，两个数间就有一个空格，数列中最后一行的数字的数量等于总行数，其中的空格等于数字数量减一
        int n = m+m-1;
        yanghui(m,n);
    }
    public static void yanghui(int m,int n){
        //定义一个二维数组存储打印的数字，以备求和（某个位置的数值）
        int[][] arr = new int[m][n];
        //给第一行处于中心位置的数字的邻左下和右下位置数赋初值，为求后面的数做基础
        //第一行中处于中心位置的数的下标是[0][m-1],所以其左下的下标是[1][m-1-1],右下的下标是[1][m+1-1]
        arr[1][m-2]=1;
        arr[1][m]=1;
        for(int i=1;i<=m;i++){
            //打印第一行，中间位置第m个数打印1，其余为空格
            if(i==1){
                for(int j=1;j<=n;j++){
                    if(j!=m){
                        System.out.print("  ");
                    }else{
                        System.out.print(1+" ");
                    }
                }
                //打印一行之后换行
                System.out.println();
            }else{
                //打印第一行之外的其他行
                for(int j=1;j<=n;j++){
                    //经观察可得每一行第一个数字的位置是总行数-（行号-1），其余有数字的位置是，前一个有数字的位置+2，该行最后一个数的位置是总行数+(行号-1)
                    //循环判断第j次打印的位置是否是有数字的位置
                    for(int a=m-(i-1);a<=m+(i-1);a=a+2){
                        //如果是，则再进行判断，否则也进行判断
                        if(j==a){
                            //判断是否是两端的数，如果是则打印1（加空格只是为了对齐），并存入数组，否则进一步计算该位置的数字
                            if(a==m-(i-1)|a==m+(i-1)){
                                arr[i-1][m-(i-1)-1]=1;
                                arr[i-1][m+(i-1)-1]=1;
                                System.out.print(1+" ");
                            }else {
                                //第i行第j列的数字=第i-1行第j-1列的数字+第i-1行第j+1列的数字
                                arr[i-1][j-1]=arr[i-2][j-2]+arr[i-2][j];
                                if(arr[i-1][j-1]<10){
                                    System.out.print(arr[i-1][j-1]+" ");
                                }else{
                                    System.out.print(arr[i-1][j-1]);
                                }
                            }
                            break;
                        }else{
                            //判断是否是循环比较的最后一个数，若是打印空格，否则继续进行循环比较
                            if(a==m+(i-1)){
                                System.out.print("  ");
                            }
                            //continue;
                        }
                    }
                }
                System.out.println();
            }
        }
    }
}

结果：